(See http://www.cs.yale.edu/homes/aspnes/classes/469/notes.pdf for a more up-to-date version of these notes.)
Collection of inequalities useful for proving upper bounds on RandomizedAlgorithms.
Contents
1. Law of total probability
If the (countably many) events { Ai } partition the probability space (i.e., they don't intersect each other and their union has probability 1), then for any event B,
![\begin{align*}
\Pr[B] = \sum \Pr[B|A_i] \Pr[A_i]
\end{align*} \begin{align*}
\Pr[B] = \sum \Pr[B|A_i] \Pr[A_i]
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_fe20560bb6a07ce683d58e6a638fff4b591e53e2_p1.png)
and for any random variable X with finite expectation,
![\begin{align*}
\E[X] = \sum \E[X|A_i] \Pr[A_i].
\end{align*} \begin{align*}
\E[X] = \sum \E[X|A_i] \Pr[A_i].
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_c396942f3e7c946bab9d69ed0446b3211f303ef8_p1.png)
This allows probabilities and expectations to be computed by case analysis, conditioning on each event Ai in turn. Pretty much every analysis of a a ProbabilisticRecurrence uses this method.
2. Union bound (Boole's inequality)
For any countable collection of events { Ai },
![\begin{align*}
\Pr\left[\bigcup A_i\right] \le \sum \Pr[A_i].
\end{align*} \begin{align*}
\Pr\left[\bigcup A_i\right] \le \sum \Pr[A_i].
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_c354c7bfa5541859db65652fee12bcca3816c44b_p1.png)
Typical use: show that if an algorithm can fail only if various improbable events occur, then the probability of failure is no greater than the sum of the probabilities of these events.
2.1. Examples
The proof of Adleman's Theorem in Derandomization.
Given a graph G = (V,E) where |V| = n and |E| = m, mark a subset of (n/2)√m vertices uniformly at random. The probability that any particular vertex is marked is then ((n/2)/√m)/n = 1/(2√m), and the probability that both endpoints of an edge are marked is (1/(2√m))((n/2)/√m - 1)/n < 1/(2√m))2 = 1/(4m). So the probability that at least one of the edges has two marked endpoints is at most m/(4m) = 1/4. We thus have a randomized algorithm that outputs an independent set of size n/(2√m) with probability 3/4, without looking at any of the edges. This is probably not an especially good independent set, but we probably can't hope to do much better without seeing the actual graph.
3. Markov's inequality
If X ≥ 0, then Pr[X ≥ α] ≤ EX/α. (See RandomVariables for proof.)
Useful for converting expectation bounds into probability bounds. Does not work in reverse: see BadCaseForMomentGeneratingFunctions.
3.1. Examples
The expected running time for randomized QuickSort is O(n log n). It follows that the probability that randomized QuickSort takes more than f(n) time is O(n log n / f(n)). For example, the probability that it performs the maximum
 = O(n2) comparisons is O(log n / n). (It's possible to do much better than this.)
= O(n2) comparisons is O(log n / n). (It's possible to do much better than this.) - Suppose we put toss m balls in n bins, uniformly and independently. What is the probability that some particular bin contains at least k balls? The probability that a particular ball lands in a particular bin is 1/n, so the expected number of balls in the bin is m/n. This gives a bound of m/nk that a bin contains k or more balls. We can combine this with the union bound to show that the probability that any bin contains k or more balls is at most m/k. Unfortunately this is not a very good bound.
4. Chebyshev's inequality
Pr[|X - EX| ≥ α] ≤ Var[X]/α2.
Proof is by applying Markov's inequality to (X-EX)2.
This is a weak concentration bound. Often useful when X is a sum of random variables, since if S = ∑ Xi, then we can calculate Var[S] = ∑ Cov(Xi, Xj) = ∑ Var[Xi] + ∑i≠j Cov(Xi,Xj), where Var[x] = E[X2] - (EX)2 and Cov(X,Y) = E[XY] - EX EY.
Note that Cov(X,Y) = 0 when X and Y are independent; this makes Chebyshev's inequality particularly useful for pairwise-independent random variables. It also works well when the Xi are indicator variables, since of E[Xi] = p, we can easily compute Var[Xi] = E[X2] - (EX)2 = p - p2 = p(1-p). This is always bounded by p, and for small p the bound is close to tight.
4.1. Examples
4.1.1. Balls in bins
Let Xi be the indicator that the i-th of m balls lands in a particular bin. Then E[Xi] = 1/n, giving E[∑ Xi] = m/n, and Var[Xi] = 1/n - 1/n2, giving Var[∑ Xi] = m/n - m/n2. So the probability that we get k + m/n or more balls in a particular bin is at most (m/n - m/n2)/k2 < m/nk2, and applying the union bound, the probability that we get k + m/n or more balls in any of the n bins is less than m/k2. Setting this equal to ε and solving for k gives a probability of at most ε of getting more than m/n + √(m/ε) balls in any of the bins. This is still not as good a bound as we can prove, but it's at least non-trivial.
4.1.2. Lazy select
This is the example from MotwaniRaghavan §3.3.
We want to find the k-th smallest element S(k) of a set S of size n. (The parentheses around the index indicate that we are considering the sorted version of the set S(1) < S(2) ... < S(n).) The idea is to:
Sample a multiset R of n3/4 elements of S with replacement and sort them. This takes O(n3/4 log n3/4) = o(n) comparisons so far.
Use our sample to find an interval that is likely to contain S(k). The idea is to pick indices l = (k-n3/4)n-1/4 and r = (k+n3/4)n-1/4 and use R(l) and R(r) as endpoints (we are omitting some floors and maxes here to simplify the notation; for a more rigorous presentation see MotwaniRaghavan). The hope is that the interval P = [R(l),R(r)] in S will both contain S(k), and be small, with |P| ≤ 4n3/4 + 2. We can compute the elements of P in 2n comparisons exactly by comparing every element with both R(l) and R(r).
- If both these conditions hold, sort P (o(n) comparisons) and return S,,(k). If not, try again.
We want to get a bound on how likely it is that P either misses S(k) or is too big.
For any fixed k, the probability that one sample in R is ≤ S(k) is exactly k/n, so the expected number X of samples ≤ S(k) is exactly kn-1/4. The variance on X can be computed by summing the variances of the indicator variables that each sample is ≤ S(k) which gives a bound Var[X] = n3/4((k/n)(1-k/n)) ≤ n3/4/4. Applying Chebyshev's inequality gives Pr[|X-kn-1/4| ≥ √n] ≤ n3/4/4n = n-1/4/4.
Now let's look at the probability that P misses S(k) because R(l) is too big, where l = kn-1/4-√n. This is
Pr[R(l) > S(k)] = Pr[X < kn-1/4-√n] ≤ n-1/4/4.
(with the caveat that we are being sloppy about round-off errors).
Similarly,
Pr[R(h) < S,,(k)] = Pr[X > kn-1/4+√n] ≤ n-1/4/4.
So the total probability that P misses S(k) is at most n-1/4/2.
Now we want to show that |P| is small. We will do so by showing that it is likely that R(l) ≥ S(k-2n^3/4^) and R(h) ≤ S(k+2n^3/4^). Let Xl be the number of samples in R that are ≤ S(k-2n^3/4^) and Xr be the number of samples in R that are ≤ S(k+2n^3/4^). Then we have E[Xl] = kn-1/4-2√n and E[Xr] = kn-1/4+2√n, and Var[Xl] and Var[Xr] are both bounded by n3/4/4.
We can now compute
Pr[R(l) < S(k-2n^3/4^)] = Pr[Xl > kn-1/4-√n] < n-1/4/4
by the same Chebyshev's inequality argument as before, and get the symmetric bound on the other side for Pr[R(r) > S,,(k+2n3/4)]. This gives a total bound of n-1/4/2 that P is too big, for a bound of n-1/4 = o(n) that the algorithm fails on its first attempt.
The total expected number of comparisons is thus given by T(n) = 2n + o(n) + O(n-1/4 T(n)) = 2n + o(n).
5. Chernoff bounds
Another application of Markov's inequality, now to exp(αS), where S = ∑ Xi and the Xi are independent.
The trick is that because the Xi are independent, so are the related variables exp(αXi), and since exp(αS) = ∏ exp(αXi) we get E[exp(αS)] = ∏ E[exp(αXi)].
The quantity E[exp(αS)], treated as a function of α, is called the moment generating function of S, because it expands into ∑k E[Xk]ak/k!, the exponential generating function (see GeneratingFunctions) for the series of k-th moments E[Xk]. Note that it may not converge for all S and α (see BadCaseForMomentGeneratingFunctions); we will be careful to choose α for which it does converge and for which Markov's inequality gives us good bounds.
5.1. The classic Chernoff bound
Let each Xi for i=1..n be a 0-1 random variable with expectation pi, so that ES = μ = ∑ pi. Then E[exp(αXi)] = pieα + (1-pi), and E[exp(αS)] = ∏ (pieα+1-pi). Let δ≥0 and α>0. Markov's inequality then gives
![\begin{align*}
\Pr\left[S \ge (1+\delta)\mu \right]
&=
\Pr\left[e^{\alpha S} \ge \exp\left(\alpha(1+\delta)\mu\right)\right]
\\
&\le
\frac{\E[e^{\alpha S}]}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\prod_{i=1}^{n} (p_i e^{\alpha}+1-p_i)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\prod_{i=1}^{n} (1 + p_i(e^\alpha - 1))}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&\le
\frac{\prod_{i=1}^{n} \exp\left(p_i(e^\alpha - 1)\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\exp\left(\sum_{i=1}^{n} p_i (e^\alpha - 1)\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\exp\left(((e^\alpha - 1) \mu\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\left(\frac{\exp\left(((e^\alpha - 1) \right)}{\exp\left(\alpha(1+\delta)\right)}\right)^\mu.
\\
&=
\left(\exp\left(e^\alpha - 1 - \alpha(1+\delta)\right)\right)^\mu.
\end{align*} \begin{align*}
\Pr\left[S \ge (1+\delta)\mu \right]
&=
\Pr\left[e^{\alpha S} \ge \exp\left(\alpha(1+\delta)\mu\right)\right]
\\
&\le
\frac{\E[e^{\alpha S}]}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\prod_{i=1}^{n} (p_i e^{\alpha}+1-p_i)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\prod_{i=1}^{n} (1 + p_i(e^\alpha - 1))}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&\le
\frac{\prod_{i=1}^{n} \exp\left(p_i(e^\alpha - 1)\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\exp\left(\sum_{i=1}^{n} p_i (e^\alpha - 1)\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\frac{\exp\left(((e^\alpha - 1) \mu\right)}{\exp\left(\alpha(1+\delta)\mu\right)}
\\
&=
\left(\frac{\exp\left(((e^\alpha - 1) \right)}{\exp\left(\alpha(1+\delta)\right)}\right)^\mu.
\\
&=
\left(\exp\left(e^\alpha - 1 - \alpha(1+\delta)\right)\right)^\mu.
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_3cedf9613b622a37c9e326ecc2104784fd812503_p1.png)
The sneaky inequality step in the middle uses the fact that (1+x) ≤ exp(x) for all x, which itself is one of the most useful inequalities you can memorize.
We now choose α to minimize the base in the last expression, by minimizing eα-1-α(1+δ). Setting the derivative with respect to α to zero gives eα = (1+δ) or α = ln (1+δ). If we plug this back into the bound, we get
![\begin{align*}
\Pr\left[S \ge (1+\delta)\mu \right]
&\le
\left(\exp\left((1 + \delta) - 1 - (1+\delta)\ln (1+\delta)\right)\right)^\mu
\\
&=
\left(\frac{e^\delta}{(1+\delta)^{1+\delta}}\right)^\mu.
\end{align*} \begin{align*}
\Pr\left[S \ge (1+\delta)\mu \right]
&\le
\left(\exp\left((1 + \delta) - 1 - (1+\delta)\ln (1+\delta)\right)\right)^\mu
\\
&=
\left(\frac{e^\delta}{(1+\delta)^{1+\delta}}\right)^\mu.
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_7ce5b657ff25a257cd5bca2d7e11a246a0bd340d_p1.png)
The base of this rather atrocious quantity is e0/11 at δ=0, and its derivative is negative for δ≥0 (the easiest way to show this is to substitute δ=x-1 first). So the bound is never greater than 1 and is less than 1 as soon as δ>0. We also have that the bound is exponential in μ for any fixed δ.
5.1.1. Variants
The full Chernoff bound can be difficult to work with. There are approximate variants that substitute a weaker but less intimidating bound. Some of the more useful are:
Pr[X ≥ (1+δ)μ] ≤ exp(-μδ2/3), when 0≤δ≤1.81 (the actual upper limit is slightly higher). Useful for small values of δ, especially because the bound can be inverted: if we want Pr[X ≥ (1+δ)μ] ≤ exp(-μδ2/3) ≤ ε, we can use any δ with
 ≤ δ ≤ 1.81. The essential idea to the proof is to show that, in the given range, exp(δ)/(1+δ)1+δ ≤ exp(-δ2/3). This is easiest to do numerically; a somewhat more formal argument that the bound holds in the range 0≤δ≤1 can be found in MitzenmacherUpfal Theorem 4.4.
≤ δ ≤ 1.81. The essential idea to the proof is to show that, in the given range, exp(δ)/(1+δ)1+δ ≤ exp(-δ2/3). This is easiest to do numerically; a somewhat more formal argument that the bound holds in the range 0≤δ≤1 can be found in MitzenmacherUpfal Theorem 4.4. Pr[X ≥ (1+δ)μ] ≤ exp(-μδ2/4), when 0≤δ≤4.11. A slightly weaker bound than the previous that holds over a larger range; this gives Pr[X ≥ (1+δ)μ] ≤ ε if
 ≤ δ ≤ 4.11. Note that the version given on p.72 of MotwaniRaghavan is not correct; it claims that the bound holds up to δ=2e-1 ≅ 4.44, but it fails somewhat short of this value.
≤ δ ≤ 4.11. Note that the version given on p.72 of MotwaniRaghavan is not correct; it claims that the bound holds up to δ=2e-1 ≅ 4.44, but it fails somewhat short of this value. Pr[X ≥ R] ≤ 2-R when R≥2eμ. Sometimes the assumption is replaced with the stronger R≥6μ (this is the version given in MitzenmacherUpfal Theorem 4.4, for example); one can also verify numerically that R≥5μ (i.e., δ≥4) is enough. The proof of the 2eμ bound is that exp(δ)/(1+δ)(1+δ) < exp(1+δ)/(1+δ)(1+δ) = (e/(1+δ))1+δ ≤ 2-(1+δ) when e/(1+δ) ≤ 1/2 or δ ≥ 2e-1. Raising this to μ gives Pr[X ≥ (1+δ)μ] ≤ 2-(1+δ)μ for δ≥2e-1. Now substitute R for (1+δ)μ (giving R≥2eμ) to get the full result. Inverting this one gives Pr[X ≥ R] ≤ ε when R ≥ min(2eμ, lg(1/ε)).
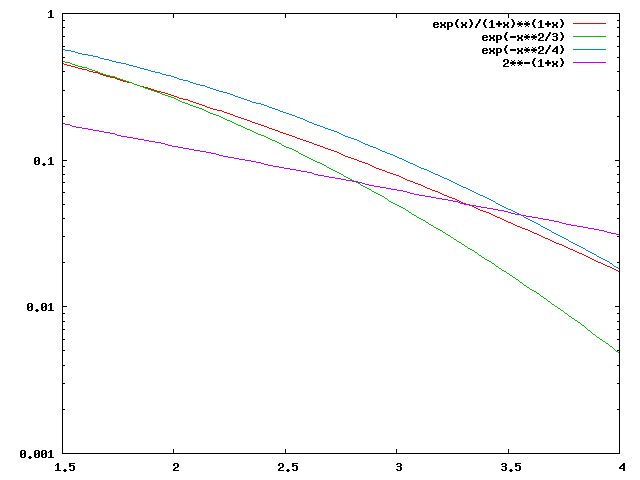
The plot below shows the relation between the various bounds for μ=1 in the region where they cross each other:
5.1.2. Applications
5.1.2.1. Balls in bins again
Let's try applying the Chernoff bound to the balls-in-bins problem. Here we let S = ∑ Xi (i=1..m) be the number of balls in a particular bin, with Xi the indicator that the i-th ball lands in the bin, EXi = pi = 1/n, and ES = μ = m/n. So the Chernoff bound gives
![\begin{align*}
\Pr[S \ge m/n + k]
&=
\Pr[S \ge (m/n) (1+kn/m)]
\\
&\le
\frac{e^{kn/m}}{(1+kn/m)^{1+kn/m}}.
\end{align*} \begin{align*}
\Pr[S \ge m/n + k]
&=
\Pr[S \ge (m/n) (1+kn/m)]
\\
&\le
\frac{e^{kn/m}}{(1+kn/m)^{1+kn/m}}.
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_cf0d5a3104ea624944cf19186e08911f47c870da_p1.png)
For m=n, this collapses to the somewhat nicer but still pretty horrifying ek/(k+1)k+1.
Staying with m=n, if we are bounding the probability of having large bins, we can use the 2-R variant to show that the probability that any particular bin has more than 2 lg n balls (for example), is at most n-2, giving the probability that there exists such a bind of at most 1/n. This is not as strong as what we can get out of the full Chernoff bound. If we take the logarithm of ek/(k+1)k+1, we get k-(k+1) ln (k+1); if we then substitute k = c ln n / ln ln n - 1, we get

So the probability of getting more than c ln n / ln ln n balls in any one bin is bounded by exp((ln n)(-c + o(1))) = n-c+o(1). This gives a maximum bin size of O(log n / log log n) with any fixed probability bound n-a for sufficiently large n.
5.1.2.2. Sums of fair coins
Suppose we flip n fair coins, and let S be the number that come up heads. We expect μ = n/2 heads on average. How many extra heads can we get, if we want to stay within a probability bound of n-c?
Here we use the small-δ approximation, which gives Pr[S ≥ (1+δ)(n/2)] ≤ exp(-δ2n/6). Setting exp(-δ2n/6) = n-c gives δ =  =
=  . The actual excess over the mean is δ(n/2) =
. The actual excess over the mean is δ(n/2) =  =
=  . By symmetry, the same bound applies to extra tails. So if we flip 1000 coins and see more than 676 heads (roughly the bound when c=3), we can reasonably conclude that either (a) our coin is biased, or (b) we just hit a rare one-in-a-billion jackpot.
. By symmetry, the same bound applies to extra tails. So if we flip 1000 coins and see more than 676 heads (roughly the bound when c=3), we can reasonably conclude that either (a) our coin is biased, or (b) we just hit a rare one-in-a-billion jackpot.
In algorithm analysis, the √((3/2)c) part usually gets absorbed into the asymptotic notation, and we just say that with probability at least 1-n-c, the sum of n random bits is within O(√(n log n)) of n/2.
5.2. Lower bound version
We can also use Chernoff bounds to show that a sum of independent random variables isn't too small. The essential idea is to repeat the upper bound argument with a negative value of α, which makes eα(1-δ)μ and increasing function in δ. The resulting bound is:
![\begin{align*}
\Pr\left[S \le (1-\delta)\mu \right]
&\le
\left(\frac{e^{-\delta}}{(1-\delta)^{1-\delta}}\right)^\mu.
\end{align*} \begin{align*}
\Pr\left[S \le (1-\delta)\mu \right]
&\le
\left(\frac{e^{-\delta}}{(1-\delta)^{1-\delta}}\right)^\mu.
\end{align*}](/pinewiki/ProbabilisticInequalities?action=AttachFile&do=get&target=latex_b62d30c92141608d9d7ae519bf0f72b61782da94_p1.png)
A simpler but weaker version of this bound is exp(-μδ2/2). Both bounds hold for all δ with 0≤δ≤1.
6. Probabilistic recurrence relations
7. Jensen's inequality
If X is a random variable and f is a convex function,1 then f(EX) ≤ E[f(X)]. See Jensen's inequality for variants, missing side conditions that exclude pathological f's and X's, and several proofs. The inequality holds in reverse when f is concave (i.e., when -f is convex).
8. Azuma-Hoeffding inequality
See Martingales.
CategoryRandomizedAlgorithmsNotes
A function f is convex if, for any x, y, and 0≤μ≤1, f(μx+(1-μ)y) ≤ μf(x)+(1-μ)f(y). One way to prove this is to show d2f/dx2 ≥ 0. (1)
