PDF version

A graph is a structure in which pairs of vertices are connected by edges. Each edge may act like an ordered pair (in a directed graph) or an unordered pair (in an undirected graph). We've already seen directed graphs as a representation for Relations; but most work in graph theory concentrates instead on undirected graphs.

Because graph theory has been studied for many centuries in many languages, it has accumulated a bewildering variety of terminology, with multiple terms for the same concept (e.g. node for vertex or arc for edge) and ambiguous definitions of certain terms (e.g., a "graph" without qualification might be either a directed or undirected graph, depending on who is using the term: graph theorists tend to mean undirected graphs, but you can't always tell without looking at the context). We will try to stick with consistent terminology to the extent that we can. In particular, unless otherwise specified, a graph will refer to a simple undirected graph: an undirected graph where each edge connects two distinct vertices (thus no self-loops) and there is at most one edge between each pair of vertices (no parallel edges).

Reasonably complete glossaries of graph theory can be found at http://www-leibniz.imag.fr/GRAPH/english/definitions.html or Glossary of graph theory. See also RosenBook Chapter 9, or BiggsBook Chapter 15 (for undirected graphs) and 18 (for directed graphs).

If you want to get a sense of the full scope of graph theory, Reinhard Diestel's (graduate) textbook Graph Theory can be downloaded from http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/download.html.

1. Types of graphs

Graphs are represented as ordered pairs G = (V,E), where V is a set of vertices and E a set of edges. The differences between different types of graphs depends on what can go in E. When not otherwise specified, we usually think of a graph as an undirected graph (see below), but there are other variants.

1.1. Directed graphs

In a directed graph or digraph, each element of E is an ordered pair, and we think of edges as arrows from a source, head, or initial vertex to a sink, tail, or terminal vertex; each of these two vertices is called an endpoint of the edge. A directed graph is simple if there is at most one edge from one vertex to another. A directed graph that has multiple edges from some vertex u to some other vertex v is called a directed multigraph.

As we saw in Relations, there is a one-to-one correspondence between simple directed graphs with vertex set V and relations on V.

1.2. Undirected graphs

In an undirected graph, each edge is a two-element subset of V. A simple undirected graph contains no duplicate edges and no loops (an edge from some vertex u back to itself). A graph with more than one edge between the same two vertices is called a multigraph. Most of the time, when we say graph, we mean a simple undirected graph.

Some authors make a distinction between pseudographs (with loops) and multigraphs (without loops), but we'll use multigraph for both.

Simple undirected graphs also correspond to relations, with the restriction that the relation must be irreflexive (no loops) and symmetric (undirected edges). This also gives a representation of undirected graphs as directed graphs, where the edges of the directed graph always appear in pairs going in opposite directions.

1.3. Hypergraphs

In a hypergraph, the edges (called hyperedges) are arbitrary nonempty sets of vertices. A k-hypergraph is one in which all such hyperedges connected exactly k vertices; an ordinary graph is thus a 2-hypergraph.

Hypergraphs are usually drawn by representing each hyperedge as a closed curve containing its members, like so:

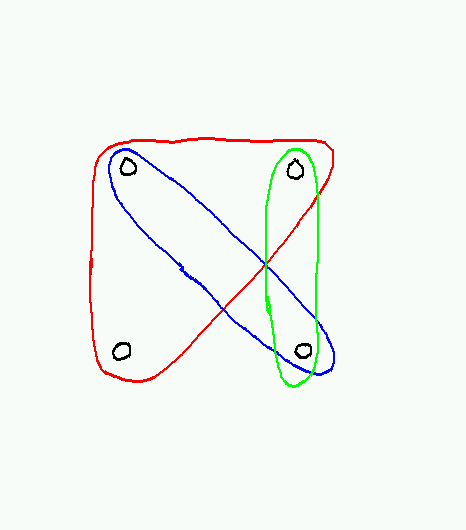
Hypergraphs aren't used very much, because it is always possible (though not always convenient) to represent a hypergraph by a bipartite graph. In a bipartite graph, the vertex set can be partitioned into two subsets S and T, such that every edge connects a vertex in S with a vertex in T. To represent a hypergraph H as a bipartite graph, we simply represent the vertices of H as vertices in S and the hyperedges of H as vertices in T, and put in an edge (s,t) whenever s is a member of the hyperedge t in H. (See also BipartiteGraphs.)

2. Examples of graphs

Any relation produces a graph, which is directed for an arbitrary relation and undirected for a symmetric relation. Examples are graphs of parenthood (directed), siblinghood (undirected), handshakes (undirected), etc.

Graphs often arise in transportation and communication networks. Here's a (now somewhat out-of-date) route map for Jet Blue airlines, taken from http://www.jetblue.com/travelinfo/routemap.html:

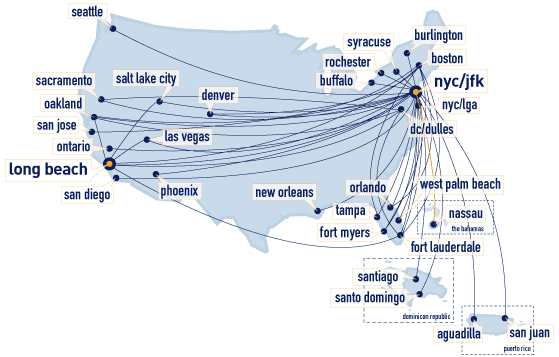
Such graphs are often labeled with edge lengths, prices, etc. In computer networking, the design of network graphs that permit efficient routing of data without congestion, roundabout paths, or excessively large routing tables is a central problem.

The web graph is a directed multigraph with web pages for vertices and hyperlinks for edges. Though it changes constantly, its properties have been fanatically studied both by academic graph theorists and employees of search engine companies, many of which are still in business. Companies such as Google base their search rankings largely on structural properties of the web graph.

Peer-to-peer systems for data sharing often have a graph structure, where each peer is a node and connections between peers are edges. The problem of designing efficient peer-to-peer systems is similar in many ways to the problem of designing efficient networks; in both cases, the structure (or lack thereof) of the underlying graph strongly affects efficiency.

3. Graph terminology

• Incidence: a vertex is incident to any edge of which it is an endpoint (and vice versa).

• Adjacency, neighborhood: two vertices are adjacent if they are the endpoints of some edge. The neighborhood of a vertex v is the set of all vertices that are adjacent to v.

• Degree, in-degree, out-degree: the degree of v counts the number edges incident to v. In a directed graph, in-degree counts only incoming edges and out-degree counts only outgoing edges (so that the degree is always the in-degree plus the out-degree). The degree of a vertex v is often abbreviated as d(v) or δ(v); in-degree and out-degree are sometimes abbreviated as d^-(v) and d⁺(v), respectively (or δ^-(v) and δ⁺(v) by people who prefer Greek).

4. Some standard graphs

• Complete graph K_n. This has n vertices, and every pair of vertices has an edge between them.

• Cycle graph C_n. This has vertices {0, 1, ... n-1} and an edge from i to i+1 for each i, plus an edge from n-1 to 0. Here n must be at least 3 to get a simple graph.

• Path P_n. This has vertices {0, 1, 2, ... n} and an edge from i to i+1 for each i. Note that n counts the number of edges rather than the number of vertices; we call the number of edges the length of the path.

• Complete bipartite graph K_mn. This has a set A of m vertices and a set B of n vertices, with an edge between every vertex in A and every vertex in B, but no edges within A or B.

• Star graphs. These have a single central vertex that is connected to n outer vertices, and are the same as K_1n.

• The cube Q_n. This is defined by letting the vertex set consist of all n-bit strings, and putting an edge between u and u' if u and u' differ in exactly one place. It can also be defined by taking the n-fold square product of an edge with itself (see below).

• Cayley graphs. The Cayley graph of a group G with a given set of generators is a labeled directed graph. The vertices of this graph are the group elements, and for each g in G and s in S there is a directed edge from g to gs labeled with s. Many common graphs are Cayley graphs with the labels (and possibly edge orientations) removed; for example, a directed cycle on m elements is the Cayley graph of ℤ_m, an n×m torus is the Cayley graph of ℤ_n×ℤ_m, and the cube Q_n is the Cayley graph of (ℤ₂)ⁿ.

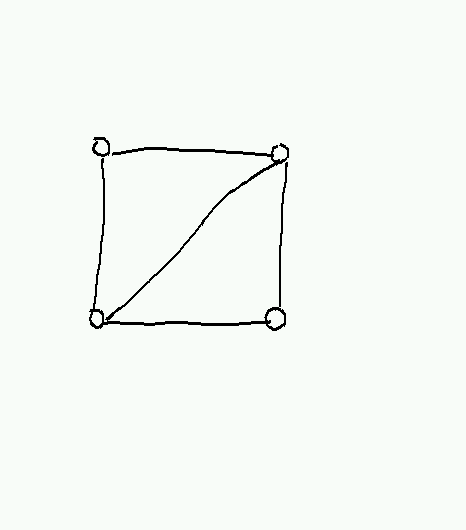
Graphs may not always be drawn in a way that makes their structure obvious. For example, here are two different presentations of Q₃, only one of which looks much like a cube:

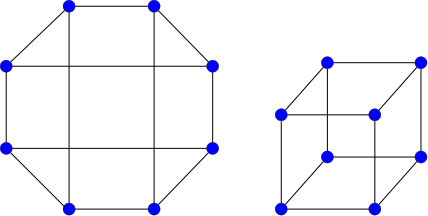
5. Operations on graphs

• Set-like operations

  • Subgraphs: G is a subgraph of H, written G ⊆ H, if V_G ⊆ V_H and E_G ⊆ E_H.

    • One can get subgraphs by deleting edges or vertices or both. Note that deleting a vertex also requires deleting any edges incident to the vertex (since we can't have an edge with a missing endpoint).

    • The maximal subgraph of a graph H whose vertex set is S is called the induced subgraph of H with vertices S. The intuition is that all edges are left in whose endpoints lie in S.

    • We will sometimes say that G is a subgraph of H if it is isomorphic to a subgraph of H, which is equivalent to having an injective homomorphism from G to H.
  • Intersections and unions are defined in the obvious way. The only tricky part is that with intersections we need to think a bit to realize this doesn't produce edges with missing endpoints.
  • Products. There are at least five different definitions of the product of two graphs used by serious graph theorists. In each case the vertex set of the product is the Cartesian product of the vertex sets, but the different definitions throw in different sets of edges. Two of them are used most often:

    • Square product (graph Cartesian product) G ◻ H. An edge (u,u')(v,v') is in G ◻ H if and only if (a) u=v and u'v' is an edge in H, or (b) uv is an edge in G and v=v'. Called the square product because the product of two (undirected) edges looks like a square. The intuition is that each vertex in G is replaced by a copy of H, and then corresponding vertices in the different copies of H are linked whenever the original vertices in G are adjacent. For algebraists, square products are popular because they behave correctly for Cayley graphs: if C₁ and C₂ are the Cayley graphs of G₁ and G₂ (for particular choices of generators), then C₁ ◻ C₂ is the Cayley graph of G₁×G₂.

      • The cube Q_n can be defined recursively by Q₁ = P₁ and Q_n = Q_n-1◻Q₁. It is also the case that Q_n=Q_k◻Q_n-k.

      • An n-by-m mesh is given by P_n-1◻P_m-1.

    • Cross product (categorical graph product) G × H. Now (u,u')(v,v') is in G × H if and only if uv is in G and u'v' is in H. In the cross product, the product of two (again undirected) edges is a cross: an edge from (u,u') to (v,v') and one from (u,v') to (v,u'). The cross product is not as useful as the square product for defining nice-looking graphs, but it can arise in some other situations. An example is when G and H describe the positions (vertices) and moves (directed edges) of two solitaire games; then the cross product G × H describes the combined game in which at each step the player must make a move in both games. (In contrast, the square product G ◻ H describes a game where the player can choose at each step to make a move in either game.)

  • Graph powers, transitive closures: see Connectivity below.

• Minors.

  • A minor of a graph G is some other graph H obtained from G by deleting edges and/or vertices (as in a subgraph) and contracting edges, where two adjacent vertices u and v are merged together into a single vertex that is connected to all of the previous neighbors of both vertices.

  • Minors are useful for recognizing certain classes of graphs. For example, a graph can be drawn in the plane without any crossing edges if and only if it doesn't contain K₅ or K_3,3 as a minor (this is known as Wagner's theorem).

• Functions from one graph to another.

  • Isomorphisms: If f:V_G→V_H is a bijection and uv ∈ E_G if and only if f(u)f(v) ∈ E_G, then G and H are said to be isomorphic and f is an isomorphism. Isomorphism is an equivalence relation—using it, we can divide graphs into equivalence classes and effectively forget the identities of the vertices. We don't currently know how to test whether two graphs are isomorphic (the Graph isomorphism problem); at the same time, we also don't know that testing isomorphism is hard, even assuming P≠NP. Graph isomorphism is a rare example of a natural problem for which we have neither a good algorithm nor a hardness proof.

  • Automorphism: An isomorphism from G to G is called an automorphism of G. Automorphisms correspond to internal symmetries of a graph. For example, the cycle C_n has 2n different automorphisms (to count them, observe there are n places we can send vertex 0 to, and having picked a place to send vertex 0 to, there are only 2 places to send vertex 1; so we have essentially n rotations times 2 for flipping or not flipping the graph). A path P_n has only 2 automorphisms (reverse the direction or not). Many graphs have no automorphisms except the identity map.

  • Homomorphisms: a homomorphism f from a graph G = (V_G, E_G) to a graph H = (V_H, E_H) is a function f:V_G→V_H such that, for all uv in E_G, f(u)f(v) is in E_H. (This definition assumes no parallel edges, but otherwise works for both directed and undirected graphs.) These are probably only of interest to category theorists.

    • Intuition: a homomorphism is a function from vertices of G to vertices of H that also maps edges to edges.
    • Example: There is a unique homomorphism from the empty graph (Ø,Ø) to any graph.

    • Example: Let G = (V,E) be an undirected graph. Then there are exactly 2 homomorphisms from P₁ to G for each edge in G.

    • Example: There is a homomorphism from G to P₁ if and only if G is bipartite. In general, there is a homomorphism from G to K_n if and only if G is n-partite (recall P₁ = K₂).

    • Comment: For multigraphs, one must define a homomorphism as a pair of functions f_V:V_G→V_H and f_E:E_G→E_H with appropriate consistency conditions.

6. Paths and connectivity

A fundamental property of graphs is connectivity: whether the graph can be divided into two or more pieces with no edges between them. Often it makes sense to talk about this in terms of reachability, or whether you can get from one vertex to another along some path.

• A path of length n in a graph is the image of a homomorphism from P_n.

  • In ordinary speech, it's a sequence of n+1 vertices v₀, v₁, ..., v_n such that v_iv_i+1 is an edge in the graph for each i.

  • A path is simple if the same vertex never appears twice (i.e. if the homomorphism is injective). If there is a path from u to v, there is a simple path from u to v obtained by removing cycles.

• If there is a path from u to v, then v is reachable from u: u →^* v. We also say that u is connected to v.

  • Easy to see that connectivity is reflexive (take a path of length 0) and transitive (paste a path from u to v together with a path from v to w to get a path from u to w). But it's not necessarily symmetric if we have a directed graph.
• Connected components

  • In an undirected graph, connectivity is symmetric, so it's an equivalence relation.

    • Equivalence classes of →^* are called the connected components of G.

    • G itself is connected iff it has a single connected component, i.e. if every vertex is reachable from every other vertex.

    • Note that isolated vertices count as (separate) connected components.
  • In a directed graph, we can make connectivity symmetric in one of two different ways:

    • Define u to be strongly connected to v if u →^* v and v →^* u. I.e. u and v are strongly connected if you can go from u to v and back again (not necessarily through the same vertices).

      • Easy to see that strong connectivity is an equivalence relation.

      • Equivalence class are called strongly-connected components.

      • G is strongly connected if it has one strongly-connected component, i.e. if every vertex is reachable from every other vertex.

    • Define u to be weakly connected to v if u →^* v in the undirected graph obtained by ignoring edge orientation.

      • Intuition is that u is weakly connected to v if there is a path from u to v if you are allowed to cross edges backwards.
      • Weakly-connected components are defined by equivalence classes; graph is weakly-connected if it has one component.
      • Weak connectivity is a "weaker" property that strong connectivity in the sense that if u is strongly connected to v, then u is weakly connected to v; but the converse does not necessarily hold.

• Power of a directed graph: k-th power G^k has same vertices as G, but uv is an edge in G^k if and only if there is a path of length k from u to v in G.

• Transitive closure of a directed graph: <>. I.e. there is an edge uv in G^* iff there is a path (of any length, including zero) from u to v in G, or in other words if u →^* v.

  • Application of powers and transitive closure of a relation, defined by R^k = R ∘ R ∘ ... R (k times) and R^* = union of R^k for all k. So →^* is the transitive closure of the directed adjacency relation →.

7. Cycles

The standard cycle graph C_n has vertices {0, 1, ..., n-1} with an edge from i to i+1 for each i and from n-1 to 0. A cycle of length n in a graph G is an image of C_n under homomorphism which includes each edge at most once. A simple cycle is a cycle that includes each vertex at most once. Cycles are often written by giving their sequence of vertices v₀v₁v₂...v_kv₀, where there is an edge from each vertex in the sequence to the following vertex. Unlike paths, which have endpoints, no vertex in a cycle has a special role.

A graph with no cycles is acyclic. Directed acyclic graphs or DAGs have the property that their reachability relation →^* is a partial order; this is easily proven by showing that if →^* is not anti-symmetric, then there is a cycle consisting of the paths between two non-anti-symmetric vertices u →^* v and v →^* u. Directed acyclic graphs may also be topologically sorted: their vertices ordered as v₀, v₁, ..., v_n-1, so that if there is an edge from v_i to v_j, then i < j. The proof is by induction on |V|, with the induction step setting v_n-1 to equal some vertex with out-degree 0 and ordering the remaining vertices recursively. (See also TopologicalSort.)

Connected acyclic undirected graphs are called trees. A connected graph G = (V,E) is a tree if and only if |E|=|V|-1; we'll prove this below.

A cycle that includes every edge exactly once is called an Eulerian cycle or Eulerian tour, after Leonhard Euler, whose study of the Seven bridges of Königsberg problem led to the development of graph theory. A cycle that includes ever vertex exactly once is called a Hamiltonian cycle or Hamiltonian tour, after William Rowan Hamilton, another historical graph-theory heavyweight (although he is more famous for inventing quaternions and the Hamiltonian). Graphs with Eulerian cycles have a simple characterization: a graph has an Eulerian cycle if and only if every vertex has even degree. Graphs with Hamiltonian cycles are harder to recognize.

8. Proving things about graphs

Suppose we want to show that all graphs or perhaps all graphs satisfying certain criteria have some property. How do we do this? In the ideal case, we can decompose the graph into pieces somehow and use induction on the number of vertices or the number of edges. If this doesn't work, we may have to look for some properties of the graph we can exploit to construct an explicit proof of what we want.

8.1. The Handshaking Lemma

This lemma relates the total degree of a graph to the number of edges. Observe that δ(v) = #{u: uv ∈ E} = ∑_{uv ∈ E} 1. So ∑_v δ(v) = ∑_v∑_{uv ∈ E} 1 = 2|E| since each edge uv is counted both as uv and as vu.

One application of the lemma is that the number of odd-degree vertices in a graph is always even.

8.2. Trees

A tree is an acyclic connected graph. We can show by induction on the number of vertices in G that G is a tree if and only if it is connected and has exactly |V|-1 edges.

We'll start with a lemma that states that G is connected only if it has at least |V|-1 edges. This avoids having to reprove this fact in the main theorem.

Lemma

Any connected graph G = (V,E) has |E| ≥ |V|-1.

Proof

By induction on |V|. The base cases are |V| = 0 and |V| = 1; in either case we have |E| ≥ 0 ≥ |V|-1.

For a larger graph G = (V,E), suppose that |E| < |V|-1; we will show that in this case G is not connected. From the handshaking lemma we have ∑_v∈V δ(v) = 2|E| < 2|V|-2. It follows that there is at least one vertex u with δ(u) ≤ 1. If δ(u) = 0, we are done: G is not connected. If δ(u) = 1, consider the graph G-{u} obtained by removing u and its incident edge. This has |E_{G-{u}| = |E| - 1 < |V}G-{u}| - 1 = |V| - 2; by the induction hypothesis, G-{u} is not connected. But since G-{u} is not connected, neither is G: if v and w are nodes with no path between them in G-{u}, then adding u doesn't help.

Now we can prove the full result:

Theorem

Let G be a nonempty connected graph. Then G is acyclic if and only if it has exactly |V|-1 edges.

Proof

1. We'll prove that a nonempty connected graph with |V|-1 edges is a tree by induction on |V|. The base case is |V| = 1 and |E| = 0; this single-vertex graph is easily seen to be acyclic. For larger |V|, from the Handshaking Lemma we have that ∑ d(v) = 2|E| = 2|V|-2. So from the Pigeonhole Principle there exists a vertex v with d(v) < 2. We can't have d(v) = 0, or G wouldn't be connected, so d(v) = 1. Now consider the graph G-v; it has |V|-1 vertices and |E|-1 = |V|-2 edges, and by the induction hypothesis, it's acyclic. Adding back v can't create any new cycles because any cycle that enters v has no edge to leave on. So G is also acyclic.

2. Now we need to show that if we have more than |V|-1 edges, some cycle exists. We'll do this by showing that an acyclic connected graph has at most |V|-1 edges, by induction on |V|. For |V| = 1 we have at most |V|-1 = 0 edges whether we are acyclic or not; this gives us the base case for free. Now consider an acyclic connected graph with |V| > 1 vertices. Choosing some vertex v₀ and construct a path v₁, v₂, ... by choosing at each step a node v_i+1 that is a neighbor of v_i and that is not already in the path. Eventually this process terminates (we only have |V| vertices to work with) with some vertex v_k. If v_k is adjacent to some vertex v_j already in the path, where j≠k-1, then we have a cycle v_j...v_k. If v_k has a neighbor that's not in the path, then we could have added it. So it follows that v_k is adjacent only to v_k-1 and has degree 1. Delete v_k to get G-v_k an acyclic graph with |V|-1 vertices and |E|-1 edges. From the induction hypothesis we have |E|-1=|V|-2 implying |E|=|V|-1 for G.

For an alternative proof based on removing edges, see BiggsBook Theorem 15.5. This also gives the useful fact that removing one edge from a tree gives exactly 2 components.

8.3. Spanning trees

Here's another induction proof on graphs. A spanning tree of a nonempty connected graph G is a subgraph of G that includes all vertices and is a tree (i.e. is connected and acyclic).

Theorem

Every nonempty connected graph has a spanning tree.

Proof

Let G = (V,E) be a nonempty connected graph. We'll show by induction on |E| that G has a spanning tree. The base case is |E| = |V|-1 (the least value for which G can be connected); then G itself is a tree (by the theorem above). For larger |E|, the same theorem gives that G contains a cycle. Let uv be any edge on the cycle, and consider the graph G-uv; this graph is connected (since we can route any path that used to go through uv around the other edges of the cycle) and has fewer edges than G, so by the induction hypothesis there is some spanning tree T of G-uv. But then T also spans G, so we are done.

8.4. Eulerian cycles

Let's prove the vertex degree characterization of graphs with Eulerian cycles. As in the previous proofs, we'll take the approach of looking for something to pull out of the graph to get a smaller case.

Theorem

Let G be a connected graph. Then G has an Eulerian cycle if and only if all nodes have even degree.

Proof

• (Only if part). Fix some cycle, and orient the edges by the direction that the cycle traverses them. Then in the resulting directed graph we must have δ^-(u) = δ⁺(u) for all u, since every time we enter a vertex we have to leave it again. But then δ(u) = 2δ⁺(u) is even.

• (If part). Suppose now that δ(u) is even for all u. We will construct an Eulerian cycle on all nodes by induction on |E|. The base case is when |E| = 2|V| and G = C_|V|. For a larger graph, choose some starting node u₁, and construct a path u₁u₂... by choosing an arbitrary unused edge leaving each u_i; this is always possible for u_i≠u₁ since whenever we reach u_i we have always consumed an even number of edges on previous visits plus one to get to it this time, leaving at least one remaining edge to leave on. Since there are only finitely many edges and we can only use each one once, eventually we must get stuck, and this must occur with u_k = u₁ for some k. Now delete all the edges in u₁...u_k from G, and consider the connected components of G-(u₁...u_k). Removing the cycle reduces δ(v) by an even number, so within each such connected component the degree of all vertices is even. It follows from the induction hypothesis that each connected component has an Eulerian cycle. We'll now string these per-component cycles together using our original cycle: while traversing u₁...,u_k when we encounter some component for the first time, we take a detour around the component's cycle. The resulting merged cycle gives an Eulerian cycle for the entire graph.

Why doesn't this work for Hamiltonian cycles? The problem is that in a Hamiltonian cycle we have too many choices: out of the δ(u) edges incident to u, we will only use two of them. If we pick the wrong two early on, this may prevent us from ever fitting u into a Hamiltonian cycle. So we would need some stronger property of our graph to get Hamiltonicity.

---

CategoryMathNotes