For more up-to-date notes see http://www.cs.yale.edu/homes/aspnes/classes/465/notes.pdf.
1. Basics
We've seen many protocols (ABD shared memory, Paxos, Chandra-Toueg) that depend on the fact that if I talk to > n/2 processes and you talk to > n/2 processes, the two groups overlap. This is a special case of a quorum system, a family of subsets of the set of processes with the property that any two subsets in the family overlap. By choosing an appropriate family, we may be able to achieve lower load on each system member, higher availability, defense against Byzantine faults, etc.
Exciting thing from a theoretical perspective is that these turn a systems problem into a combinatorial problem ⇒ we can ask combinatorialists how to solve it.
2. Simple quorum systems
- Majority and weighted majorities
- Specialized read/write systems where write quorum is a column and read quorum a row of some grid.
Dynamic quorum systems: get > 1/2 of most recent copy.
Crumbling walls (optimal small-quorum system for good choice of wall sizes, see http://wisdomarchive.wisdom.weizmann.ac.il:81/archive/00000020/).
3. Goals
Minimize quorum size.
Minimize load, defined as min over all access strategies (probability distributions on quorums) of max over all servers of probability it gets hit.
Maximize capacity, defined as number of quorum accesses per time unit in the limit if each quorum access ties up a quorum member for 1 time unit (but we are allowed to stagger a quorum access over multiple time units).
Maximize fault-tolerance: minimum number of server failures that blocks all quorums. Note that for standard quorum systems this is directly opposed to minimizing quorum size, since killing the smallest quorum stops us dead.
Minimize failure probability = probability that every quorum contains at least one bad server, assuming each server fails with independent probability.
Naor and Wool (The Load, Capacity and Availability of Quorum Systems, SIAM J. on Computing, April 1998 (naorwool.pdf)) describes trade-offs between these goals (some of these were previously known, see the paper for citations):
- capacity = 1/load; this is obtained by selecting the quorums independently at random according to the load-minimizing distribution. In particular this means we can forget about capacity and just concentrate on minimizing load.
- load ≥ max(min quorum size / n, 1/min quorum size). The first case is obvious: if every access hits c nodes, spreading them out as evenly as possible still hits each node c/n of the time. The second is trickier: Naor and Wool prove it using LP duality, but the argument essentially says that if we have some quorum Q of size c, then since every quorum intersects Q in at least one place, we can show that every quorum Q' adds at least 1 unit of load in total to the members of Q. So if we pick a random quorum Q', the average load added to all of Q is at least 1, so the average load added to some element of Q is at least 1/|Q| = 1/c. Combining the two cases, we can't hope to get load better than 1/√n, and to get this load we need quorums of size at least √n.
failure probability is at least p when p > 1/2 (and optimal system is to just pick a single leader in this case), failure probability can be made exponentially small in size of smallest quorum when p < 1/2 (with many quorums). These results are due to Peleg and Wool http://citeseer.ist.psu.edu/peleg93availability.html.
4. Paths system
Optimal-load system from Naor and Wool with exponentially low failure probability, based on percolation theory.
The basic idea is to build a d×d mesh-like graph where a quorum consists of the union of a top-to-bottom path (TB path) and a left-to-right path (LR path); this gives quorum size O(√n) and load O(1/√n).
The actual mesh is a little more complicated. Here is a picture of the d=3 case from the Naor and Wool paper:
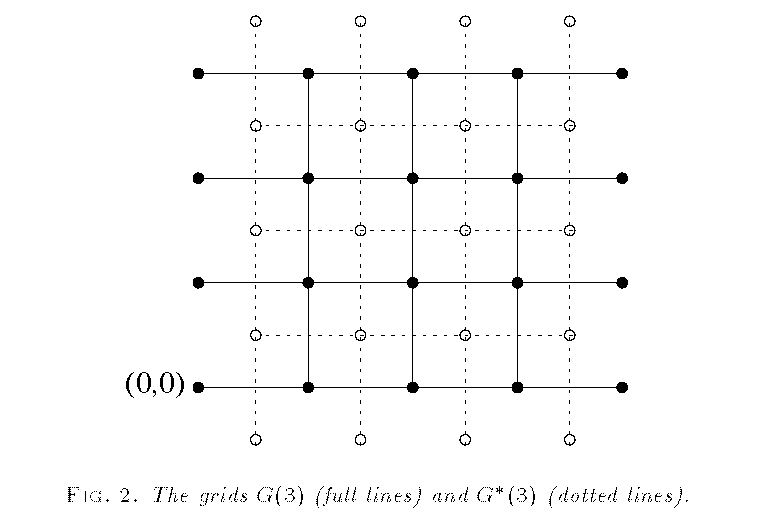
Each server corresponds to an pair of intersecting edges, one from the G(d) grid and one from the G*(d) grid (the star indicates that G*(d) is the dual graph of G(d)). A quorum consists of a set of servers that produce an LR path in G(d) and a TB path in G*(d). Quorums intersect, because any LR path in G(d) must cross some TB path in G*(d) at some server (in fact, each pair of quorums intersects in at least two places). The total number of elements n is (d+1)2 and the minimum size of a quorum is 2d+1 = Θ(√n).
The symmetry of the mesh gives that there exists a LR path in the mesh if and only if there does not exist a TB path in its complement, the graph that has an edge only if the mesh doesn't. For a mesh with failure probability p < 1/2, the complement is a mesh with failure probability q = 1-p > 1/2. Using results in percolation theory, it can be shown that for failure probability q > 1/2, the probability that there exists a left-to-right path is exponentially small in d (formally, for each p there is a constant φ(p) such that Pr[∃ LR path] ≤ exp(-φ(q)d)). We then have Pr[∃ live quorum] = Pr[∃ TB path ∧ ∃ LR path] = Pr[¬∃ LR path in complement ∨ ¬∃ TB path in complement] ≤ Pr[¬∃ LR path in complement] + Pr[¬∃ TB path in complement] ≤ 2 exp(-φ(1-p)d) = = 2 exp(-Θ(√n)). So the failure probability of this system is exponentially small for any fixed p < 1/2.
See paper (naorwool.pdf) for more details.
5. Byzantine quorum systems
Standard quorum systems are great when you only have crash failures, but with Byzantine failures you have to worry about finding a quorum that includes a Byzantine serve who lies about the data. For this purpose you need something stronger. Following Malkhi and Reiter 1997 and Malkhi et al 2001 one can define:
A b-disseminating quorum system guarantees |Q1∩Q2| ≥ b+1 for all quorums Q1 and Q2. This guarantees that if I update a quorum Q1 and you update a quorum Q2, and there are at most b Byzantine processes, then there is some non-Byzantine process in both our quorums. Mostly useful if data is "self-verifying" e.g. signed with digital signatures that the Byzantine processes can't forge. Otherwise, I can't tell which of the allegedly most recent data values is the right one since the Byzantine processes lie.
A b-masking quorum system guarantees |Q1∩Q2| ≥ 2b+1 for all quorums Q1 and Q2. (In other words, it's the same as a 2b-disseminating quorum system.) This allows me to defeat the Byzantine processes through voting: given 2b+1 overlapping servers, if I want the most recent value of the data I take the one with the most recent timestamp that appears on at least b+1 servers, which the Byzantine guys can't fake.
An additional requirement in both cases is that for any set of servers B with |B| ≤ b, there is some quorum Q such that Q∩B = ∅. This prevents the Byzantine processes from stopping the system by simply refusing to participate.
Note: these definitions are based on the assumption that there is some fixed bound on the number of Byzantine processes. Malkhi and Reiter in the 1997 paper give more complicated definitions for the case where one has an arbitrary family { B } of potential Byzantine sets. The definitions above are actually simplified versions from the 2001 paper.
The simplest way to build a b-disseminating quorum system is to use supermajorities of size at least (n+b+1)/2; the overlap between any two such supermajorities is at least (n+b+1)-n = b+1. This gives a load of substantially more than ½. There are better constructions that knock the load down to Θ(√((b+1)/n)); see the Malkhi et al paper for pointers.
For more on this see this very recent survey by Merideth and Reiter.
6. Probabilistic quorum systems
The problem with all standard (or "strict") quorum systems is that we need big quorums to get high fault tolerance, since the adversary can always stop us by knocking out our smallest quorum. A probabilistic quorum system or more specifically an ε-intersection quorum system Malkhi et al 2001 improves the fault-tolerance by relaxing the requirements. For such a system we have not only a set system Q, but also a probability distribution w supplied by the quorum system designer, with the property that Pr[Q1∩Q2 = ∅] ≤ ε when Q1 and Q2 are chosen independently according to their weights.
6.1. Example
Let a quorum be any set of size k√n for some k and let all quorums be chosen uniformly at random. Pick some quorum Q1; what is the probability that a random Q2 does not intersect Q1? Imagine we choose the elements of Q2 one at a time. The chance that the first element x1 of Q2 misses Q1 is exactly (n-k√n)/n = 1 - k/√n, and conditioning on x1 through xi-1 missing Q1 the probability that xi also misses it is (n-k√n-i+1)/(n-i+1) ≤ (n-k√n)/n = 1 - k/√n. So taking the product over all i gives Pr[all miss Q1] ≤ (1-k/√n)k√n ≤ exp(-(k√n)(k/√n)) = exp(-k2). So by setting k = Θ(ln 1/ε), we can get our desired ε-intersecting system.
6.2. Performance
Failure probabilities, if naively defined, can be made arbitrarily small: add low-probability singleton quorums that are hardly ever picked unless massive failures occur. But the resulting system is still ε-intersecting.
One way to look at this is that it points out a flaw in the ε-intersecting definition: ε-intersecting quorums may cease to be ε-intersecting conditioned on a particular failure pattern (e.g. when all the non-singleton quorums are knocked out by massive failures). But Malkhi et al address the problem in a different way, by considering only survival of high quality quorums, where a particular quorum Q is δ-high-quality if Pr[Q1∩Q2 = ∅ | Q1 = Q] ≤ δ and high quality if it's √ε-high-quality. It's not hard to show that a random quorum is δ-high-quality with probability at least ε/δ, so a high quality quorum is one that fails to intersect a random quorum with probability at most √ε and a high quality quorum is picked with probability at least 1-√ε.
We can also consider load; Malkhi et al show that essentially the same bounds on load for strict quorum systems also hold for ε-intersecting quorum systems: load(S) ≥ max((E(|Q|)/n, (1-√ε)2/E(|Q|)), where E(|Q|) is the expected size of a quorum. The left-hand branch of the max is just the average load applied to a uniformly-chosen server. For the right-hand side, pick some high quality quorum Q' with size less than or equal to (1-√ε)E(|Q|) and consider the load applied to its most loaded member by its nonempty intersection (which occurs with probability at least 1-√ε) with a random quorum.
7. Signed quorum systems
A further generalization of probabilistic quorum systems is signed quorum systems Haifeng Yu, Signed quorum systems, PODC 2004. In these systems, a quorum consists of some set of positive members (servers you reached) and negative members (servers you tried to reach but couldn't). These allow O(1)-sized quorums while tolerating n-O(1) failures, under certain natural probabilistic assumptions. Because the quorums are small, the load on some servers may be very high: so these are most useful for fault-tolerance rather than load-balancing. See the paper for more details.
