PDF version

1. Matrices

We've seen that a sequence a₁, a₂, ..., a_n is really just a function from some index set ({1..n} in this case) to some codomain, where a_i = a(i) for each i. What if we have two index sets? Then we have a two-dimensional structure:

where A_ij = a(i,j) and the domain of the function is just the cross-product of the two index sets. Such a structure is called a matrix. The values A_ij are called the elements or entries of the matrix. A sequence of elements with the same first index is called a row of the matrix; similarly, a sequence of elements with the same second index is called a column. The dimension of the matrix specifies the number of rows and the number of columns: the matrix above has dimension (3,2), or, less formally, it is a 3×2 matrix.¹ A matrix is square if it has the same number of rows and columns.

Note: The convention in matrix indices is to count from 1 rather than 0. In ComputerScience terms, matrices are written in FORTRAN.

By convention, variables representing matrices are usually written with capital letters. (This is to distinguish them from lower-case scalars, which are single numbers.)

1.1. Interpretation

We can use a matrix any time we want to depict a function of two arguments (over small finite sets if we want it to fit on one page). A typical example (that predates the formal notion of a matrix by centuries) is a table of distances between cities or towns, such as this example from 1807:²

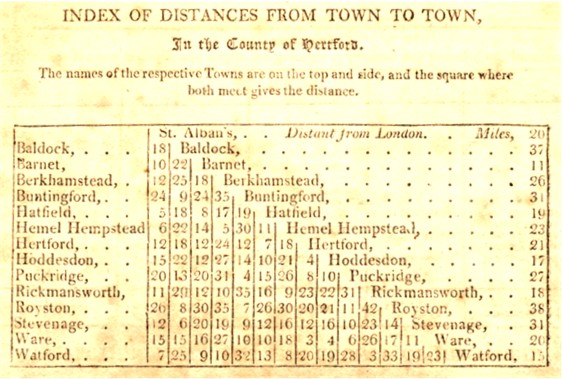
Because distance matrices are symmetric (see below), usually only half of the matrix is actually printed.

Another example would be a matrix of counts. Suppose we have a set of destinations D and a set of origins O. For each pair (i,j) ∈ D×O, let C_ij be the number of different ways to travel from j to i. For example, let origin 1 be Bass Library, origin 2 be AKW, and let destinations 1, 2, and 3 be Bass, AKW, and SML. Then there is 1 way to travel between Bass and AKW (walk), 1 way to travel from AKW to SML (walk), and 2 ways to travel from Bass to SML (walk above-ground or below-ground). If we assume that we are not allowed to stay put, there are 0 ways to go from Bass to Bass or AKW to AKW, giving the matrix

Wherever we have counts, we can also have probabilities. Suppose we have a particle that moves between positions 1..n by flipping a coin, and moving up with probability ½ and down with probability ½ (staying put if it would otherwise move past the endpoints). We can describe this process by a transition matrix P whose entry P_ij gives the probability of moving to i starting from j. For example, for n = 4, the transition matrix is

Finally, the most common use of matrices in linear algebra is to represent the coefficients of a linear transformation, which we will describe later.

1.2. Operations on matrices

1.2.1. Transpose of a matrix

The transpose of a matrix A, written A' or A^T, is obtained by reversing the indices of the original matrix; (A')_ij = A_ji for each i and j. This has the effect of turning rows into columns and vice versa:

If a matrix is equal to its own transpose (i.e., if A_ij = A_ji for all i and j), it is said to be symmetric. The transpose of an n×m matrix is an m×n matrix, so only square matrices can be symmetric.

1.2.2. Sum of two matrices

If we have two matrices A and B with the same dimension, we can compute their sum A+B by the rule (A+B)_ij = A_ij+B_ij. Another way to say this is that matrix sums are done term-by-term: there is no interaction between entries with different indices.

For example, suppose we have the matrix of counts C above of ways of getting between two destinations on the Yale campus. Suppose that upperclassmen are allowed to also take the secret Science Hill Monorail from the sub-basement of Bass Library to the sub-basement of AKW. We can get the total number of ways an upperclassman can get from each origin to each destination by adding to C a second matrix M giving the paths involving monorail travel:

1.2.3. Product of two matrices

Suppose we are not content to travel once, but have a plan once we reach our destination in D to travel again to a final destination in some set F. Just as we constructed the matrix C (or C+M, for monorail-using upperclassmen) counting the number of ways to go from each point in O to each point in D, we can construct a matrix Q counting the number of ways to go from each point in D to each point in F. Can we combine these two matrices to compute the number of ways to travel O→D→F?

The resulting matrix is known as the product QC. We can compute each entry in QC by taking a sum of products of entries in Q and C. Observe that the number of ways to get from k to i via some single intermediate point j is just Q_ijC_jk. To get all possible routes, we have to sum over all possible intermediate points, giving (QC)_ik = ∑_j Q_ijC_jk.

This gives the rule for multiplying matrices in general: to get (AB)_ik, sum A_ijB_jk over all intermediate values j. This works only when the number of columns in A is the same as the number of rows in B (since j has to vary over the same range in both matrices), i.e. when A is an n×m matrix and B is an m×s matrix for some n, m, and s. If the dimensions of the matrices don't match up like this, the matrix product is undefined. If the dimensions do match, they are said to be compatible.

For example, let B = (C+M) from the sum example and let A be the number of ways of getting from each of destinations 1 = Bass, 2 = AKW, and 3 = SML to final destinations 1 = Heaven and 2 = Hell. After consulting with appropriate representatives of the Divinity School, we determine that one can get to either Heaven or Hell from any intermediate destination in one way by dying (in a state of grace or sin, respectively), but that Bass Library provides the additional option of getting to Hell by digging. This gives a matrix

We can now compute the product

One special matrix I (for each dimension n×n) has the property that IA = A and BI = B for all matrices A and B with compatible dimension. This matrix is known as the identity matrix, and is defined by the rule I_ii = 1 and I_ij = 0 for i≠j. It is not hard to see that in this case (IA)_ij = ∑_k I_ikA_kj = I_iiA_ij = A_ij, giving IA = A; a similar computation shows that BI = B. With a little more effort (omitted here) we can show that I is the unique matrix with this identity property.

1.2.4. The inverse of a matrix

A matrix A is invertible if there exists a matrix A^-1 such that AA^-1 = A^-1A = 1. This is only possible if A is square (because otherwise the dimensions don't work) and may not be possible even then. Note that it is enough to find a matrix such that A^-1A = I.

To try to invert a matrix, we start with the pair of matrices A, I (where I is the identity matrix defined above) and multiply both sides of the pair from the left by a sequence of transformation matrices B₁, B₂, ... B_k until B_kB_k-1⋯B₁A = I. At this point the right-hand matrix will be B_kB_k-1⋯B₁ = A^-1. (We could just keep track of all the B_i, but it's easier to keep track of their product.)

How do we pick the B_i? These will be matrices that (a) multiply some row by a scalar, (b) add a multiple of one row to another row, or (c) swap two rows. We'll use the first kind to make all the diagonal entries equal one, and the second kind to get zeroes in all the off-diagonal entries. The third kind will be saved for emergencies, like getting a zero on the diagonal.

That the operations (a), (b), and (c) correspond to multiplying by a matrix is provable but tedious.³ Given these operations, we can turn any invertible matrix A into I by working from the top down, rescaling each row i using a type (a) operation to make A_ii = 1, then using a type (b) operation to subtract A_ji times row i from each row j > i to zero out A_ji, then finally repeating the same process starting at the bottom to zero out all the entries above the diagonal. The only way this can fail is if we hit some A_ii = 0, which we can swap with a nonzero A_ji if one exists (using a type (c) operation). If all the rows from i on down have a zero in the i column, then the original matrix A is not invertible. This entire process is known as Gauss-Jordan elimination.

This procedure can be used to solve matrix equations: if AX = B, and we know A and B, we can compute X by first computing A^-1 and then multiplying X = A^-1AX = A^-1B. If we are not interested in A^-1 for its own sake, we can simplify things by substituting B for I during the Gauss-Jordan elimination procedure; at the end, it will be transformed to X.

1.2.4.1. Example

Original A is on the left, I on the right.

and we're done. (It's probably worth multiplying the original A by the alleged A^-1 to make sure that we didn't make a mistake.)

1.2.5. Scalar multiplication

Suppose we have a matrix A and some constant c. The scalar product cA is given by the rule (cA)_ij = cA_ij; in other words, we multiply (or scale) each entry in A by c. The quantity c in this context is called a scalar; the term scalar is also used to refer to any other single number that might happen to be floating around.

Note that if we only have scalars, we can pretend that they are 1×1 matrices; a+b = a₁₁ + b₁ and ab = a₁₁b₁₁. But this doesn't work if we multiply a scalar by a matrix, since cA (where c is considered to be a matrix) is only defined if A has only one row. Hence the distinction between matrices and scalars.

1.3. Matrix identities

For the most part, matrix operations behave like scalar operations, with a few important exceptions:

1. Matrix multiplication is only defined for matrices with compatible dimensions.

2. Matrix multiplication is not commutative: in general, we do not expect that AB = BA. This is obvious when one or both of A and B is not square (one of the products is undefined because the dimensions aren't compatible), but it's also true even if A and B are both square. For a simple example of a non-commutative pair of matrices, consider

On the other hand, matrix multiplication is associative: A(BC) = (AB)C. The proof is by expansion of the definition. First compute (A(BC))_ij = ∑_k A_ik(BC)_kj = ∑_k∑_m A_ikB_kmC_mj. Then compute ((AB)C)_ij = ∑_m (AB)_imC_mj = ∑_m∑_k A_ikB_kmC_mj = ∑_k∑_m A_ikB_kmC_mj = (A(BC))_ij.

So despite the limitations due to non-compatibility and non-commutativity, we still have:

Associative laws

A+(B+C) = (A+B)+C (easy), (AB)C = A(BC) (see above). Also works for scalars: c(AB) = (cA)B = A(cB) and (cd)A = c(dA) = d(cA).

Distributive laws

A(B+C) = AB+BC, A(B+C) = AB+AC. Also works for scalars: c(A+B) = cA+cB, (c+d)A = cA+dA.

Additive identity

A+0 = 0+A = A, where 0 is the all-zero matrix of the same dimension as A.

Multiplicative identity

AI = A, IA = A, 1A = A, A1 = A, where I is the identity matrix of appropriate dimension in each case and 1 is the scalar value 1.

Inverse of a product

(AB)^-1 = B^-1A^-1. Proof: (B^-1A^-1)(AB) = B^-1(A^-1A)B = B^-1(IB) = B^-1B = I, and similarly for (AB)(B^-1A^-1).

Transposes

(A+B)' = A'+B' (easy), (AB)' = B'A' (a little trickier). (A^-1)' = (A')^-1, provided A^-1 exists (proof: A'(A^-1)' = (A^-1A)' = I' = I).

Using these identities, we can do arithmetic on matrices without knowing what their actual entries are, so long as we are careful about non-commutativity. So for example we can compute

• (A+B)² = (A+B)(A+B) = A²+AB+BA+B².

Similarly, if for square A we have

• S = ∑_n∈ℕ Aⁿ,

(where A⁰=I) we can solve the equation

• S = I + AS

by first subtracting AS from both sides to get

• IS - AS = I

then applying the distributive law:

• (I-A)S = I

and finally multiplying both sides from the left by (I-A)^-1 to get

• S = (I-A)^-1,

assuming I-A is invertible.

2. Vectors

A 1×n or n×1 matrix is called a vector. A 1×n matrix is called a row vector for obvious reasons; similarly, an n×1 matrix is called a column vector.

Vectors behave exactly like matrices in every respect; however, they are often written with lowercase letters to distinguish them from their taller and wider cousins. If this will cause confusion with scalars, we can disambiguate by writing vectors with a little arrow on top:

or in boldface: x. Often we will just hope it will be obvious from context which variables represent vectors and which represent scalars, since writing all the little arrows can take a lot of time.

When extracting individual coordinates from a vector, we omit the boring index and just write x₁, x₂, etc. This is done for both row and column vectors, so rather than write x'_i we can just write x_i.

2.1. Geometric interpretation

We can use a vector to represent the coordinates of a point in space. In general, given some point in the n-dimensional Euclidean space ℝⁿ, we consider it as an n×1 column vector (row vectors work too, but the convention is to use column vectors because it makes the matrix-vector product Ax look like function application). The set of all such vectors for a given fixed dimension form a vector space.

For example, we could represent the latitude and longitude of the major world landmarks Greenwich Observatory, Mecca, and Arthur K. Watson Hall by the column vectors

Pedantic note: The surface of the Earth is not really a Euclidean space, despite the claims of the Flat Earth Society.

In running text, we can represent these column vectors as transposed row vectors, e.g. [21.45 39.82]' for the coordinates of Mecca. Quite often we will forget whether we are dealing with a column vector or a row vector specifically and just write the sequence of entries, e.g. (21.54 39.82) or (21.54, 39.82).

We can use vectors to represent any quantities that can be expressed as a sequence of coordinates in ℝ (or more generally, over any field: see AlgebraicStructures and AbstractLinearAlgebra). A common use is to represent offsets—the difference between the coordinates of two locations—and velocities—the rate at which the coordinates of a moving object change over time. So, for example, we might write the velocity of a car that is moving due northeast at 100 km/h as the vector (100/√2 100/√2)', where each entry corresponds to the speed if we look only at the change in the north-south or west-east position. We can also think of coordinates of points as themselves offsets from some origin at position 0—Greenwich Observatory in the case of latitude and longitude.

2.2. Sums of vectors

We can add vectors term-by-term just as we can add any other matrices. For vectors representing offsets (or velocities) the geometric interpretation of x+y is that we attach y to the end of x (or vice versa, since addition is commutative) and take the combined offset, as in this picture:

        *
       /^
      / |
     /  |
 x+y/   |y
   /    |
  /     |
 /      |
0——————>*
    x

This can be used to reduce the complexity of pirate-treasure instructions:

1. Yargh! Start at the olde hollow tree on Dead Man's Isle, if ye dare.

2. Walk 10 paces north.
3. Walk 5 paces east.
4. Walk 20 paces south.
5. Walk 6√2 paces northwest.
6. Dig 8 paces down.
7. Climb back up 6 paces. There be the treasure, argh!

In vector notation, this becomes:

1. (0 0 0)'
2. + (10 0 0)'
3. + (0 5 0)'
4. + (-20 0 0)'
5. + (6 -6 0)'
6. + (0 0 -8)'
7. + (0 0 6)

which sums to (-4 -1 -2)'. So we can make our life easier by walking 4 paces south, 1 pace west, and digging only 2 paces down.

2.3. Length

The length of a vector x, usually written as ‖x‖ or sometimes just |x|, is defined as √(∑_i x_i); the definition follows from the Pythagorean theorem (length)² = ∑ (coordinates)². Because the coordinates are squared, all vectors have non-negative length, and only the zero vector has length 0.

Length interacts with scalar multiplication exactly as you would expect: ‖cx‖ = c‖x‖. The length of the sum of two vectors depends on how the are aligned with each other, but the triangle inequality ‖x+y‖ ≤ ‖x‖+‖y‖ always holds.

A special class of vectors are the unit vectors, those vectors x for which ‖x‖ = 1. In geometric terms, these correspond to all the points on the surface of a radius-1 sphere centered at the origin. Any vector x can be turned into a unit vector x/‖x‖ by dividing by its length. In two dimensions, the unit vectors are all of the form (x y)' = (cos Θ, sin Θ)', where by convention Θ is the angle from due east measured counterclockwise; this is why traveling 9 units northwest corresponds to the vector 9(cos 135°, sin 135°)' = (-9/√2, 9/√2)'. In one dimension, the unit vectors are (±1). (There are no unit vectors in zero dimensions: the unique zero-dimensional vector has length 0.)

2.4. Dot products and orthogonality

Suppose we have some column vector x, and we want to know how far x sends us in a particular direction, where the direction is represented by a unit column vector e. We can compute this distance (a scalar) by taking the dot product

• e⋅x = e'x = ∑ e_ix_i.

For example, x = (3 4)' and e = (1 0)', then the dot product is

In this case we see that the (1 0)' vector conveniently extracts the first coordinate, which is about what we'd expect. But we can also find out how far x takes us in the (1/√2 1/√2)' direction: this is (1/√2 1/√2)x = 7/√2.

By convention, we are allowed to take the dot product of two row vectors or of a row vector times a column vector or vice versa, provided of course that the non-boring dimensions match. In each case we transpose as appropriate to end up with a scalar when we take the matrix product.

Nothing in the definition of the dot product restricts either vector to be a unit vector. If we compute x⋅y where x = ce and ‖e‖ = 1, then we are effectively multiplying e⋅y by c. It follows that the dot product is proportional to the length of both of its arguments. This often is expressed in terms of the geometric formulation, memorized by vector calculus students since time immemorial:

• The dot product of x and y is equal to the product of their lengths times the cosine of the angle between them.

This formulation is a little misleading, since modern geometers will often define the angle between two vectors x and y as cos^-1(x⋅y/(‖x‖⋅‖y‖)), but it gives a good picture of what is going on. One can also define the dot-product as the area of the parallelogram with sides x and y, with the complication that if the parallelogram is flipped upside-down we treat the area as negative. The simple version in terms of coordinates is harder to get confused about, so we'll generally stick with that.

Two vectors are orthogonal if their dot product is zero. In geometric terms, this occurs when either one or both vectors is the zero vector or when the angle between them is ±90° (since cos(±90°) = 0). In other words, two non-zero vectors are orthogonal if and only if they are perpendicular to each other.

Orthogonal vectors satisfy the Pythagorean theorem: If x⋅y = 0, then ‖x+y‖² = (x+y)⋅(x+y) = x⋅x + x⋅y + y⋅x + y⋅y = x⋅x + y⋅y = ‖x‖² + ‖y‖². It is not hard to see that the converse is also true: any pair of vectors for which ‖x+y‖² = ‖x‖² + ‖y‖² must be orthogonal (at least in ℝⁿ).

Orthogonality is also an important property of vectors used to define coordinate systems, as we will see below.

3. Linear combinations and subspaces

A linear combination of a set of vectors x₁...x_n is any vector that can be expressed as ∑ c_ix_i for some coefficients c_i. The span of the vectors, written <x₁...x_n>, is the set of all linear combinations of the x_i.⁴

The span of a set of vectors forms a subspace of the vector space, where a subspace is a set of vectors that is closed under linear combinations. This is a succinct way of saying that if x and y are in the subspace, so is ax+by for any scalars a and b. We can prove this fact easily: if x = ∑ c_ix_i and y = ∑ d_ix_i, then ax+by = ∑ (ac_i+bd_i)x_i.

A set of vectors x₁, x₂, ..., x_n is linearly independent if there is no way to write one of the vectors as a linear combination of the others, i.e. if there is no choice of coefficients that makes some x_i = ∑_j≠i c_jx_j. An equivalent definition is that there is no choice of coefficients c_i such that ∑ c_ix_i = 0 and at least one c_i is nonzero (to see the equivalence, subtract x_i from both sides of the x_i = ∑ c_jx_j equation).

3.1. Bases

If a set of vectors is both (a) linearly independent, and (b) spans the entire vector space, then we call that set of vectors a basis of the vector space. An example of a basis is the standard basis consisting of the vectors (0 0 ... 0 1)', (0 0 ... 1 0)', ..., (0 1 ... 0 0)', (1 0 ... 0 0)'. This has the additional nice property of being made of of vectors that are all orthogonal to each other (making it an orthogonal basis) and of unit length (making it a normal basis).

A basis that is both orthogonal and normal is called orthonormal. We like orthonormal bases because we can recover the coefficients of some arbitrary vector v by taking dot-products. If v = ∑ a_ix_i, then v⋅x_j = ∑ a_i(x_i⋅x_j) = a_i, since orthogonality means that x_i⋅x_j=0 when i≠j, and normality means x_i⋅x_i = ‖x_i‖² = 1.

However, even for non-orthonormal bases it is still the case that any vector can be written as a unique linear combination of basis elements. This fact is so useful we will state it as a theorem:

Theorem

If {x_i} is a basis for some vector space V, then every vector y has a unique representation y = a₁x₁ + a₂x₂ + ... + a_nx_n.

Proof

Suppose there is some y with more than one representation, i.e. there are sequences of coefficients a_i and b_i such that y = a₁x₁ + a₂x₂ + ... + a_nx_n = b₁x₁ + b₂x₂ + ... + b_nx_n. Then 0 = y-y = a₁x₁ + a₂x₂ + ... + a_nx_n - b₁x₁ + b₂x₂ + ... + b_nx_n = (a₁-b₁)x₁ + (a₂-b₂)x₂ + ... + (a_n-b_n)x_n. But since the x_i are independent, the only way a linear combination of the x_i can equal 0 is if all coefficients are 0, i.e. if a_i = b_i for all i.

Even better, we can do all of our usual vector space arithmetic in terms of the coefficients a_i. For example, if a = ∑a_ix_i and b = ∑b_ix_i, then it can easily be verified that a+b = ∑(a_i+b_i)x_i and ca = ∑(ca_i)x_i.

However, it may be the case that the same vector will have different representations in different bases. For example, in ℝ², we could have a basis B₁ = { (1,0), (0,1) } and a basis B₂ = { (1,0), (1,-2) }. The vector (2,3) would be represented as (2,3) using basis B₁ but would be represented as (5/2,-3/2) in basis B₂. In the standard basis { (1,0), (0,1) }, the representation of (2,3) is just (2,3).

Both bases above have the same size. This is not an accident; if a vector space has a finite basis, then all bases have the same size. We'll state this as a theorem, too:

Theorem

Let x₁...x_n and y₁...y_m be two finite bases of the same vector space V. Then n=m.

Proof

Assume without loss of generality that n ≤ m. We will show how to replace elements of the x_i basis with elements of the y_i basis to produce a new basis consisting only of y₁...y_n. Start by considering the sequence y₁,x₁...x_n. This sequence is not independent since y₁ can be expressed as a linear combination of the x_i (they're a basis). So from Theorem 1 there is some x_i that can be expressed as a linear combination of y₁,x₁...x_i-1. Swap this x_i out to get a new sequence y₁,x₁...x_i-1,x_i+1,...x_n. This new sequence is also a basis, because (a) any z can be expressed as a linear combination of these vectors by substituting the expansion of x_i into the expansion of z in the original basis, and (b) it's independent, because if there is some nonzero linear combination that produces 0 we can substitute the expansion of x_i to get a nonzero linear combination of the original basis that produces 0 as well. Now continue by constructing the sequence y₂,y₁,x₁...x_i-1,x_i+1,...x_n, and arguing that some x_i' in this sequence must be expressible as a combination of earlier terms by Theorem 1 (it can't be y₁ because then y₂y₁ is not independent), and drop this x_i'. By repeating this process we can eventually eliminate all the x_i, leaving the basis y_n,...,y₁. But then any y_k for k > n would be a linear combination of this basis, so we must have m = n.

The size of any basis of a vector space is called the dimension of the space.

4. Linear transformations

When we multiply a column vector by a matrix, we transform the vector into a new vector. This transformation is linear in the sense that A(x+y) = Ax + Ay and A(cx) = cAx; thus we call it a linear transformation. Conversely, any linear function f from column vectors to column vectors can be written as a matrix M such that f(x) = Mx. We can prove this by decomposing each x using the standard basis.

Theorem

Let f:ℝⁿ→ℝ^m be a linear transformation. Then there is a unique n×m matrix M such that f(x) = Mx for all column vectors x.

Proof

We'll use the following trick for extracting entries of a matrix by multiplication. Let M be an n×m matrix, and let eⁱ be a column vector with eⁱ_j = 1 if i=j and 0 otherwise.⁵ Now observe that (eⁱ)'Me^j = ∑_k eⁱ_k (Me^j)_k = (Me^j)_i = ∑_k M_ike^j_k = M_ij. So given a particular linear f, we will now define M by the rule M_ij = (eⁱ)'f(e^j). It is not hard to see that this gives f(e^j) = Me^j for each basis vector j, since multiplying by (eⁱ)' grabs the i-th coordinate in each case. To show that Mx = f(x) for all x, decompose each x as ∑_k c_ke^k. Now compute f(x) = f(∑_k c_ke^k) = ∑_k c_kf(e^k) = ∑_k c_kM(e^k) = M(∑_k c_ke^k) = Mx.

4.1. Composition

What happens if we compose two linear transformations? We multiply the corresponding matrices:

• (g∘f)(x) = g(f(x)) = g(M_fx) = M_g(M_fx) = (M_gM_f)x.

This gives us another reason why the dimensions have to be compatible to take a matrix product: If multiplying by an n×m matrix A gives a map g:ℝ^m→ℝⁿ, and multiplying by a k×l matrix B gives a map f:ℝ^l→ℝ^k, then the composition g∘f corresponding to AB only works if m = k.

4.2. Role of rows and columns of M in the product Mx

When we multiply a matrix and a column vector, we can think of the matrix as a sequence of row or column vectors and look at how the column vector operates on these sequences.

Let M_i⋅ be the i-th row of the matrix (the "⋅" is a stand-in for the missing column index). Then we have

• (Mx)_i = ∑_k M_ikx_k = M_i⋅⋅x.

So we can think of Mx as a vector of dot-products between the rows of M and x:

Alternatively, we can work with the columns M_⋅j of M. Now we have

• (Mx)_i = ∑_k M_ikx_k = ∑_k (M_⋅k)_ix_k.

From this we can conclude that Mx is a linear combination of columns of M: Mx = ∑_k x_kM_⋅k. Example:

The set {Mx} for all x is thus equal to the span of the columns of M; it is called the column space of M.

For yM, where y is a row vector, similar properties hold: we can think of yM either as a row vector of dot-products of y with columns of M or as a weighted sum of rows of M; the proof follows immediately from the above facts about a product of a matrix and a column vector and the fact that yM = (M'y')'. The span of the rows of M is called the row space of M, and equals the set {yM} of all results of multiplying a row vector by M.

4.3. Geometric interpretation

Geometrically, linear transformations can be thought of as changing the basis vectors for a space: they keep the origin in the same place, move the basis vectors, and rearrange all the other vectors so that they have the same coordinates in terms of the new basis vectors. These new basis vectors are easily read off of the matrix representing the linear transformation, since they are just the columns of the matrix. So in this sense all linear transformations are transformations from some vector space to the column space of some matrix.⁶

This property makes linear transformations popular in graphics, where they can be used to represent a wide variety of transformations of images. Below is a picture of an untransformed image (top left) together with two standard basis vectors labeled x and y. In each of the other images, we have shifted the basis vectors using a linear transformation, and carried the image along with it.⁷

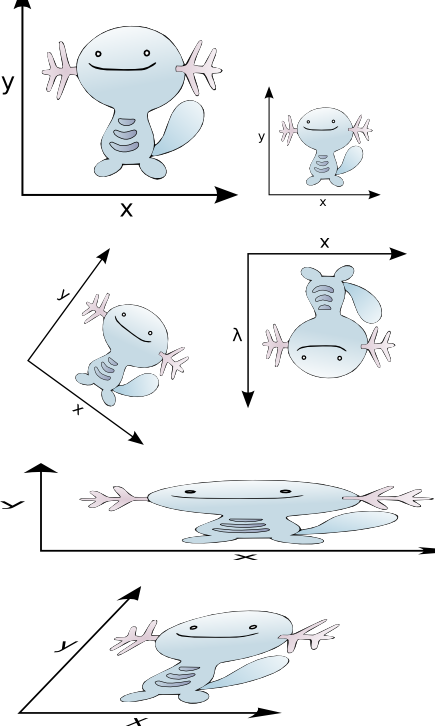
Note that in all of these transformations, the origin stays in the same place. If you want to move an image, you need to add a vector to everything. This gives an affine transformation, which is any transformation that can be written as f(x) = Ax+b for some matrix A and column vector b.

Many two-dimensional linear transformations have standard names. The simplest transformation is scaling, where each axis is scaled by a constant, but the overall orientation of the image is preserved. In the picture above, the top right image is scaled by the same constant in both directions and the second-from-the-bottom image is scaled differently in each direction.

Recall that the product Mx corresponds to taking a weighted sum of the columns of M, with the weights supplied by the coordinates of x. So in terms of our basis vectors x and y, we can think of a linear transformation as specified by a matrix whose columns tell us what vectors for replace x and y with. In particular, a scaling transformation is represented by a matrix of the form

where s_x is the scale factor for the x (first) coordinate and s_y is the scale factor for the y (second) coordinate. Flips (as in the second image from the top on the right] are a special case of scaling where one or both of the scale factors is -1.

A more complicated transformation, as shown in the bottom image, is a shear. Here the image is shifted by some constant amount in one coordinate as the other coordinate increases. Its matrix looks like this:

Here the x vector is preserved: (1, 0) maps to the first column (1, 0), but the y vector is given a new component in the x direction of c, corresponding to the shear. If we also flipped or scaled the image at the same time that we sheared it, we could represent this by putting values other than 1 on the diagonal.

For a rotation, we will need some trigonometric functions to compute the new coordinates of the axes as a function of the angle we rotate the image by. The convention is that we rotate counterclockwise: so in the figure above, the rotated image is rotated counterclockwise approximately 315° or -45°. If Θ is the angle of rotation, the rotation matrix is given by

For example, when Θ = 0°, then we have cos Θ = 1 and sin Θ = 0, giving the identity matrix. when Θ = 90°, then cos Θ = 0 and sin Θ = 1, so we rotate the x axis to the vector (cos Θ, sin Θ) = (0, 1) and the y axis to (-sin Θ, cos Θ) = (-1, 0). This puts the x axis pointing north where the y axis used to be, and puts the y axis pointing due west.

4.4. Rank and inverses

The dimension of the column space of a matrix—or, equivalently, the dimension of the range of the corresponding linear transformation—is called the rank. The rank of a linear transformation determines, among other things, whether it has an inverse.

Claim

If f:ℝⁿ→ℝ^m is a linear transformation with an inverse f^-1, then we can show all of the following:

1. f^-1 is also a linear transformation.

2. n = m, and f has full rank, i.e., rank(f) = rank(f^-1) = m.

Proof

1. Let x and y be elements of codomain(f) and let a be a scalar. Then f(af^-1(x)) = a(f(f^-1(x))) = ax, implying that f^-1(ax) = af^-1(x). Similarly, f(f^-1(x)+f^-1(y)) = f(f^-1(x)) + f(f^-1(y)) = x+y, giving f^-1(x+y) = f^-1(x) + f^-1(y). So f^-1 is linear.

2. Suppose n < m. Pick any basis eⁱ for ℝⁿ, and observe that { f(eⁱ) } spans range(f) (since we can always decompose x as ∑ a_ieⁱ to get f(x) = ∑ a_if(eⁱ)). So the dimension of range(f) is at most n. If n < m, then range(f) is a proper subset of ℝ^m (otherwise it would be m-dimensional). This implies f is not surjective and thus has no inverse. Alternatively, if m < n, use the same argument to show that any claimed f^-1 isnt. By the same argument, if either f or f^-1 does not have full rank, it's not surjective.

The converse is also true: If f:ℝⁿ→ℝⁿ has full rank, it has an inverse. The proof of this is to observe that if dim(range(f)) = n, then range(f) = ℝⁿ (since ℝⁿ has no full-dimensional subspaces). So in particular we can take any basis { eⁱ } for ℝⁿ and find corresponding { xⁱ } such that f(xⁱ) = eⁱ. Now the linear transformation that maps ∑ a_ieⁱ to ∑ a_ixⁱ is an inverse for f, since f(∑ a_ixⁱ) = ∑ a_if(x_i) = ∑ a_ieⁱ.

4.5. Projections

Suppose we are given a low-dimensional subspace of some high-dimensional space (e.g. a line (dimension 1) passing through a plane (dimension 2)), and we want to find the closest point in the subspace to a given point in the full space. The process of doing this is called projection, and essentially consists of finding some point z such that (x-z) is orthogonal to any vector in the subspace.

Let's look at the case of projecting onto a line first, then consider the more general case.

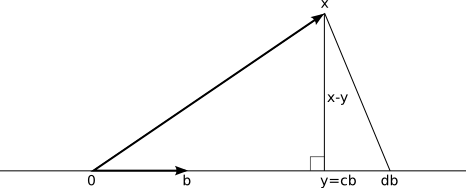
A line consists of all points that are scalar multiples of some fixed vector b. Given any other vector x, we want to extract all of the parts of x that lie in the direction of b and throw everything else away. In particular, we want to find a vector y = cb for some scalar c, such that (x-y)⋅b = 0. This is is enough information to solve for c.

We have (x-cb)⋅b = 0, so x⋅b = c(b⋅b) or c = (x⋅b)/(b⋅b). So the projection of x onto the subspace { cb | c ∈ ℝ } is given by y = b(x⋅b)/(b⋅b) or y = b(x⋅b)/‖b‖². If b is normal (i.e. if ‖b‖ = 1), then we can leave out the denominator; this is one reason we like orthonormal bases so much.

Why is this the right choice to minimize distance? Suppose we pick some other vector db instead. Then the points x, cb, and db form a right triangle with the right angle at cb, and the distance from x to db is ‖x-db‖ = √(‖x-cb‖²+‖cb-db‖²) ≥ ‖x-cb‖.

But now what happens if we want to project onto a larger subspace? For example, suppose we have a point x in three dimensions and we want to project it onto some plane of the form { c₁b₁ + c₂b₂ }, where b₁ and b₂ span the plane. Here the natural thing to try is to send x to y = b₁(x⋅b₁)/‖b₁‖² + b₂(x⋅b₂)/‖b₂‖². We then want to argue that the vector (x-y) is orthogonal to any vector of the form c₁b₁ + c₂b₂. As before, (x-y) is orthogonal to any vector in the plane, it's orthogonal to the difference between the y we picked and some other z we didn't pick, so the right-triangle argument again shows it gives the shortest distance.

Does this work? Let's calculate: (x-y)⋅(c₁b₁ + c₂b₂) = x⋅(c₁b₁ + c₂b₂) - (b₁(x⋅b₁)/‖b₁‖² + b₂(x⋅b₂)/‖b₂‖²)⋅(c₁b₁ + c₂b₂) = c₁(x⋅b₁ - (b₁⋅b₁)(x⋅b₁)/(b₁⋅b₁)) + c₂(x⋅b₂ - (b₂⋅b₂)(x⋅b₂)/(b₂⋅b₂)) - c₁(b₁⋅b₂)(x⋅b₁)/(b₁⋅b₁) - c₂(b₁⋅b₂)(x⋅b₂)/(b₂⋅b₂). The first two terms cancel out very nicely, just as in the one-dimensional case, but then we are left with a nasty (b₁⋅b₂)(much horrible junk) term at the end. It didn't work!

So what do we do? We could repeat our method for the one-dimensional case and solve for c₁ and c₂ directly. This is probably a pain in the neck. Or we can observe that the horrible extra term includes a (b₁⋅b₂) factor, and if b₁ and b₂ are orthogonal, it disappears. The moral: We can project onto a 2-dimensional subspace by projecting independently onto the 1-dimensional subspace spanned by each basis vector, provided the basis vectors are orthogonal. And now we have another reason to like orthonormal bases.

This generalizes to subspaces of arbitrary high dimension: as long as the b_i are all orthogonal to each other, the projection of x onto the subspace <b_i> is given by ∑ b_i(x⋅b_i)/‖b_i‖². Note that we can always express this as matrix multiplication by making each row of a matrix B equal to one of the vectors b_i/‖b_i‖²; the product Bx then gives the coefficients for the basis elements in the projection of x, since we have already seen that multiplying a matrix by a column vector corresponds to taking a dot product with each row. If we want to recover the projected vector ∑ c_ib_i we can do so by taking advantage of the fact that multiplying a matrix by a column vector also corresponds to taking a linear combination of columns: this gives a combined operation of B'Bx which we can express as a single projection matrix P = B'B. So projection corresponds to yet another special case of a linear transformation.

One last detail: suppose we aren't given orthonormal b_i but are instead given some arbitrary non-orthogonal non-normal basis for the subspace. Then what do we do?

The trick here is to use a technique called Gram-Schmidt orthogonalization. This constructs an orthogonal basis from an arbitrary basis by induction. At each step, we have a collection of orthogonalized vectors b₁...b_k and some that we haven't processed yet a_k+1...a_m; the induction hypothesis says that the b₁...b_k vectors are (a) orthogonal and (b) span the same subspace as a₁...a_k. The base case is the empty set of basis vectors, which is trivially orthogonal and also trivially spans the subspace consisting only of the 0 vector. We add one new vector to the orthogonalized set by projecting a_k+1 to some point c on the subspace spanned by b₁...,b_k; we then let b_k+1 = a_k+1-c. This new vector is orthogonal to all of b₁...b_k by the definition of orthogonal projection, giving a new, larger orthogonal set b₁...b_k+1. These vectors span the same subspace as a₁...a_k+1 because we can take any vector x expressed as ∑ c_ia_i, and rewrite it as ∑[i=1..k] c_ib_i + c_k+1(c+b_k+1), and in the second term c_k+1c reduces to a linear combination of b₁...b_k; the converse essentially repeats this argument in reverse. It follows that when the process completes we have an orthogonal set of vectors b₁...b_m that span precisely the same subspace as a₁...a_m, and we have our orthogonal basis. (But not orthonormal: if we want it to be orthonormal, we divide each b_i by ‖b_i‖ as well.)

5. Further reading

Linear algebra is vitally important in ComputerScience: it is a key tool in graphics, scientific computing, robotics, neural networks, and many other areas. If you do further work in these areas, you will quickly find that we have not covered anywhere near enough linear algebra in this course. Your best strategy for remedying this deficiency may be to take an actual linear algebra course; failing that, a very approachable introductory text is Linear Algebra and Its Applications, by Gilbert Strang. You can also watch an entire course of linear algebra lectures through YouTube: http://www.youtube.com/view_play_list?p=E7DDD91010BC51F8.

Some other useful books on linear algebra:

• Golub and van Loan, Matrix Computations. Picks up where Strang leaves off with practical issues in doing computation.

• Halmos, Finite-Dimensional Vector Spaces. Good introduction to abstract linear algebra, i.e. properties of vector spaces without jumping directly to matrices.

Matlab (which is available on the Zoo machines: type matlab at a shell prompt) is useful for playing around with operations on matrices. There are also various non-commercial knockoffs like Scilab or Octave that are not as comprehensive as Matlab but are adequate for most purposes. Note that with any of these tools, if you find yourselves doing lots of numerical computation, it is a good idea to talk to a numerical analyst about round-off error: the floating-point numbers inside computers are not the same as real numbers, and if you aren't careful about how you use them you can get very strange answers.

---

CategoryMathNotes