This file was hand-built from CS202/Notes on 2005-11-17, and may since have become out of date.
Contents
- WhyYouShouldKnowAboutMath
- So why do I need to learn all this nasty mathematics?
- But isn't math hard?
- Thinking about math with your heart
- WhatYouShouldKnowAboutMath
- Foundations and logic
- Fundamental mathematical objects
- Modular arithmetic and polynomials
- Linear algebra
- Graphs
- Counting
- Probability
- Tools
- PropositionalLogic
- PredicateLogic
- InferenceRules
- ProofTechniques
- SetTheory
- Naive set theory
- Operations on sets
- Axiomatic set theory
- Cartesian products, relations, and functions
- Constructing the universe
- Sizes and arithmetic
- Further reading
- NaturalNumbers
- Axioms
- Order properties
- PeanoAxioms
- InductionProofs
- Simple induction
- Strong induction
- Recursion
- Structural induction
- SummationNotation
- Summations
- Computing sums
- Products
- Other big operators
- RelationsAndFunctions
- StructuralInduction
- SolvingRecurrences
- The problem
- Guess but verify
- Converting to a sum
- The Master Theorem
- PigeonholePrinciple
- HowToCount
- What counting is
- Basic counting techniques
- Applying the rules
- An elaborate counting problem
- Further reading
- BinomialCoefficients
- Recursive definition
- Vandermonde's identity
- Sums of binomial coefficients
- Application: the inclusion-exclusion formula
- Negative binomial coefficients
- Fractional binomial coefficients
- Further reading
- GeneratingFunctions
- Basics
- Some standard generating functions
- More operations on formal power series and generating functions
- Counting with generating functions
- Generating functions and recurrences
- Recovering coefficients from generating functions
- Asymptotic estimates
- Recovering the sum of all coefficients
- A recursive generating function
- Summary of operations on generating functions
- Variants
- Further reading
- ProbabilityTheory
- History and interpretation
- Probability axioms
- Probability as counting
- Independence and the intersection of two events
- Union of two events
- Conditional probability
- Random variables
- RandomVariables
- Random variables
- The distribution of a random variable
- The expectation of a random variable
- The variance of a random variable
- Probability generating functions
- Summary: effects of operations on expectation and variance of random variables
- The general case
- Relations
- Relations, digraphs, and matrices
- Operations on relations
- Classifying relations
- Equivalence relations
- Partial orders
- Closure
- GraphTheory
- Types of graphs
- Examples of graphs
- Graph terminology
- Some standard graphs
- Operations on graphs
- Paths and connectivity
- Cycles
- Proving things about graphs
- BipartiteGraphs
- Bipartite matching
- NumberTheory
- Divisibility and division
- Greatest common divisors
- The Fundamental Theorem of Arithmetic
- Modular arithmetic and residue classes
- DivisionAlgorithm
- ModularArithmetic
- ChineseRemainderTheorem
- GroupTheory
- Some common groups
- Arithmetic in groups
- Subgroups
- Homomorphisms and isomorphisms
- Cartesian products
- How to understand a group
- Subgroups, cosets, and quotients
- Homomorphisms, kernels, and the First Isomorphism Theorem
- Generators and relations
- Decomposition of abelian groups
- SymmetricGroup
- Why it's a group
- Cycle notation
- The role of the symmetric group
- Permutation types, conjugacy classes, and automorphisms
- Odd and even permutations
- AlgebraicStructures
- What algebras are
- Why we care
- Cheat sheet: axioms for algebras (and some not-quite algebras)
- Classification of algebras with a single binary operation (with perhaps some other operations sneaking in later)
- Operations on algebras
- Algebraic structures with more binary operations
- Polynomials
- Division of polynomials
- Divisors and greatest common divisors
- Factoring polynomials
- The ideal generated by an irreducible polynomial
- FiniteFields
- A magic trick
- Fields and rings
- Polynomials over a field
- Algebraic field extensions
- Applications
- LinearAlgebra
- Matrices
- Vectors
- Linear combinations and subspaces
- Linear transformations
- Further reading
1. WhyYouShouldKnowAboutMath
2. So why do I need to learn all this nasty mathematics?
Why you should know about mathematics, if you are interested in ComputerScience: or, more specifically, why you should take CS202 or a comparable course:
- Computation is something that you can't see and can't touch, and yet (thanks to the efforts of generations of hardware engineers) it obeys strict, well-defined rules with astonishing accuracy over long periods of time.
- Computations are too big for you to comprehend all at once. Imagine printing out an execution trace that showed every operation a typical $500 desktop computer executed in one (1) second. If you could read one operation per second, for eight hours every day, you would die of old age before you got halfway through. Now imagine letting the computer run overnight.
So in order to understand computations, we need a language that allows us to reason about things we can't see and can't touch, that are too big for us to understand, but that nonetheless follow strict, simple, well-defined rules. We'd like our reasoning to be consistent: any two people using the language should (barring errors) obtain the same conclusions from the same information. Computer scientists are good at inventing languages, so we could invent a new one for this particular purpose, but we don't have to: the exact same problem has been vexing philosophers, theologians, and mathematicians for much longer than computers have been around, and they've had a lot of time to think about how to make such a language work. Philosophers and theologians are still working on the consistency part, but mathematicians (mostly) got it in the early 20th-century. Because the first virtue of a computer scientist is laziness, we are going to steal their code.
3. But isn't math hard?
Yes and no. The human brain is not really designed to do formal mathematical reasoning, which is why most mathematics was invented in the last few centuries and why even apparently simple things like learning how to count or add require years of training, usually done at an early age so the pain will be forgotten later. But mathematical reasoning is very close to legal reasoning, which we do seem to be unusually good at. There is very little structural difference between the sentences
- "If x is in S, then x+1 is in S." (1)
and
- "If x is of royal blood, then x's child is of royal blood." (2)
but because the first is about boring numbers and the second is about fascinating social relationships and rules, most people have a much easier time deducing that to show somebody is royal we need to start with some known royal and follow a chain of descendants than they have deducing that to show that some number is in the set S. we need to start with some known element of S and show that repeatedly adding 1 gets us to the number we want. And yet to a logician these are the same processes of reasoning.
So why is statement (1) trickier to think about than statement (2)? Part of the difference is familiarity—we are all taught from an early age what it means to be somebody's child, to take on a particular social role, etc. For mathematical concepts, this familiarity comes with exposure and practice, just as with learning any other language. But part of the difference is that we humans are wired to understand and appreciate social and legal rules: we are very good at figuring out the implications of a (hypothetical) rule that says that any contract to sell a good to a consumer for $100 or more can be cancelled by the consumer within 72 hours of signing it provided the good has not yet been delivered, but we are not so good at figuring out the implications of a rule that says that a number is composite if and only if it is the product of two integer factors neither of which is 1. It's a lot easier to imagine having to cancel a contract to buy swampland in Florida that you signed last night while drunk than having to prove that 82 is composite. But again: there is nothing more natural about contracts than about numbers, and if anything the conditions for our contract to be breakable are more complicated than the conditions for a number to be composite.
4. Thinking about math with your heart
There are two things you need to be able to do to get good at mathematics (the creative kind that involves writing proofs, not the mechanical kind that involves grinding out answers according to formulas). One of them is to learn the language: to attain what mathematicians call mathematical maturity. You'll do that in CS202, if you pay attention. But the other is to learn how to activate the parts of your brain that are good at mathematical-style reasoning when you do math—the parts evolved to detect when the other primates in your primitive band of hunter-gatherers are cheating.
To do this it helps to get a little angry, and imagine that finishing a proof or unraveling a definition is the only thing that will stop your worst enemy from taking some valuable prize that you deserve. (If you don't have a worst enemy, there is always the UniversalQuantifier.) But whatever motivation you choose, you need to be fully engaged in what you are doing. Your brain is smart enough to know when you don't care about something, and if you don't believe that thinking about math is important, it will think about something else.
5. WhatYouShouldKnowAboutMath
List of things you should know about if you want to do ComputerScience.
6. Foundations and logic
Why: This is the assembly language of mathematics—the stuff at the bottom that everything else complies to.
- Propositional logic.
- Predicate logic.
- Axioms, theories, and models.
- Proofs.
- Induction and recursion.
7. Fundamental mathematical objects
Why: These are the mathematical equivalent of data structures, the way that more complex objects are represented.
- Naive set theory.
- Predicates vs sets.
- Set operations.
- Set comprehension.
- Russell's paradox and axiomatic set theory.
- Functions.
- Functions as sets.
- Injections, surjections, and bijections.
- Cardinality.
- Finite vs infinite sets.
- Sequences.
- Relations.
- Equivalence relations, equivalence classes, and quotients.
- Orders.
- The basic number tower.
- Countable universes: ℕ, ℤ, ℚ. (Can be represented in a computer.)
- Uncountable universes: ℝ, ℂ. (Can only be approximated in a computer.)
- Other algebras.
- The string monoid.
- ℤ/m and ℤ/p.
- Polynomials over various rings and fields.
8. Modular arithmetic and polynomials
Why: Basis of modern cryptography.
- Arithmetic in ℤ/m.
- Primes and divisibility.
- Euclid's algorithm and inverses.
- The Chinese Remainder Theorem.
- Fermat's Little Theorem and Euler's Theorem.
- RSA encryption.
- Galois fields and applications.
9. Linear algebra
Why: Shows up everywhere.
- Vectors and matrices.
- Matrix operations and matrix algebra.
- Geometric interpretations.
- Inverse matrices and Gaussian elimination.
10. Graphs
Why: Good for modeling interactions. Basic tool for algorithm design.
- Definitions: graphs, digraphs, multigraphs, etc.
- Paths, connected components, and strongly-connected components.
- Special kinds of graphs: paths, cycles, trees, cliques, bipartite graphs.
- Subgraphs, induced subgraphs, minors.
11. Counting
Why: Basic tool for knowing how much resources your program is going to consume.
- Basic combinatorial counting: sums, products, exponents, differences, and quotients.
- Combinatorial functions.
- Factorials.
- Binomial coefficients.
- The 12-fold way.
- Advanced counting techniques.
- Inclusion-exclusion.
- Recurrences.
- Generating functions.
12. Probability
Why: Can't understand randomized algorithms or average-case analysis without it. Handy if you go to Vegas.
- Discrete probability spaces.
- Events.
- Independence.
- Random variables.
- Expectation and variance.
- Probabilistic inequalities.
- Markov's inequality.
- Chebyshev's inequality.
- Chernoff bounds.
- Stochastic processes.
- Markov chains.
- Martingales.
- Branching processes.
13. Tools
Why: Basic computational stuff that comes up, but doesn't fit in any of the broad categories above. These topics will probably end up being mixed in with the topics above.
These you will have seen before:
- How to differentiate and integrate simple functions.
- Things you may have forgotten about exponents and logarithms.
These may be somewhat new:
- Inequalities and approximations.
- ∑ and ∏ notation.
- Computing or approximating the value of a sum.
- Asymptotics.
14. PropositionalLogic
15. PredicateLogic
16. InferenceRules
17. ProofTechniques
18. SetTheory
Set theory is the dominant foundation for mathematics. The idea is that everything else in mathematics—numbers, functions, etc.—can be written in terms of sets, so that if you have a consistent description of how sets behave, then you have a consistent description of how everything built on top of them behaves. If predicate logic is the machine code of mathematics, set theory would be assembly language.
Contents
19. Naive set theory
Naive set theory is the informal version of set theory that corresponds to our intuitions about sets as unordered collections of objects (called elements) with no duplicates. A set can be written explicitly by listing its elements using curly braces:
{ } = the empty set ∅, which has no elements.
{ Moe, Curly, Larry } = the Three Stooges.
- { 0, 1, 2, ... } = ℕ, the natural numbers. Note that we are relying on the reader guessing correctly how to continue the sequence here.
- { { }, { 0 }, { 1 }, { 0, 1 }, { 0, 1, 2 }, 7 } = a set of sets of natural numbers, plus a stray natural number that is directly an element of the outer set.
Membership in a set is written using the ∈ symbol (pronounced "is an element of" or "is in"). So we can write Moe ∈ The Three Stooges or 4 ∈ ℕ. We can also write ∉ for "is not an element of", as in Moe ∉ ℕ.
A fundamental axiom in set theory is that the only distinguishing property of a set is its list of members: if two sets have the same members, they are the same set.
For nested sets like { { 1 } }, ∈ represents only direct membership: the set { { 1 } } only has one element, { 1 }, so 1 ∉ { { 1 } }. This can be confusing if you think of ∈ as representing the English "is in," because if I put my lunch in my lunchbox and put my lunchbox in my backpack, then my lunch is in my backpack. But my lunch is not an element of { { my lunch }, my textbook, my slingshot }. In general, ∈ is not transitive (see Relations)—it doesn't behave like < unless there is something very unusual about the set you are applying it to—and there is no particular notation for being a deeply-buried element of an element of an element (etc.) of some set.
In addition to listing the elements of a set explicitly, we can also define a set by set comprehension, where we give a rule for how to generate all of its elements. This is pretty much the only way to define an infinite set without relying on guessing, but can be used for sets of any size. Set comprehension is usually written using set-builder notation, as in the following examples:
{ x | x∈ℕ ∧ x > 1 ∧ ∀y∈ℕ∀z∈ℕ yz = x ⇒ y = 1 ∨ z = 1 } = the prime numbers.
- { 2x | x∈ℕ } = the even numbers.
{ x | x∈ℕ ∧ x < 12 } = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 }.
Sometimes the original set that an element has to be drawn from is put on the left-hand side of the pipe:
{ n∈ℕ | ∃x,y,z∈ℕ x > 0 ∧ y > 0 ∧ xn + yn = zn }. (This is a fancy name for the two-element set { 1, 2 }; see Fermat's Last Theorem.)
Using set comprehension, we can see that every set in naive set theory is equivalent to some predicate. Given a set S, the corresponding predicate is x∈S, and given a predicate P, the corresponding set is { x | Px }. But beware of Russell's paradox: what is { S | S∉S }?
20. Operations on sets
If we think of sets as representing predicates, each logical connective gives rise to a corresponding operation on sets:
A∪B = { x | x∈A ∨ x∈B }. The union of A and B.
A∩B = { x | x∈A ∧ x∈B }. The intersection of A and B.
A∖B = { x | x∈A ∧ x∉B }. The set difference of A and B.
A∆B = { x | x∈A ⊕ x∈B }. The symmetric difference of A and B.
(Of these, union and intersection are the most important in practice.)
Corresponding to implication is the notion of a subset:
- A⊆B ("A is a subset of B") if and only if ∀x x∈A ⇒ x∈B.
Sometimes one says A is contained in B if A⊆B. This is one of two senses in which A can be "in" B—it is also possible that A is in fact an element of B (A∈B). For example, the set A = { 12 } is an element of the set B = { Moe, Larry, Curly, { 12 } } but A is not a subset of B, because A's element 12 is not an element of B. Usually we will try to reserve "is in" for ∈ and "is contained in" for ⊆, but it's safest to use the symbols to avoid any possibility of ambiguity.
Finally we have the set-theoretic equivalent of negation:
Ā = { x | x∉A }. The set Ā is known as the complement of A.
If we allow complements, we are necessarily working inside some fixed universe: the complement of the empty set contains all possible objects. This raises the issue of where the universe comes from. One approach is to assume that we've already fixed some universe that we understand (e.g. ℕ), but then we run into trouble if we want to work with different classes of objects at the same time. Modern set theory is defined in terms of a collection of axioms that allow us to construct, essentially from scratch, a universe big enough to hold all of mathematics without apparent contradictions while avoiding the paradoxes that may arise in naive set theory.
21. Axiomatic set theory
The problem with naive set theory is that unrestricted set comprehension is too strong, leading to contradictions. Axiomatic set theory fixes this problem by being more restrictive about what sets one can form. The axioms most commonly used are known as Zermelo-Fraenkel set theory with choice or ZFC. The page AxiomaticSetTheory covers these axioms in painful detail, but in practice you mostly just need to know what constructions you can get away with.
The short version is that you can construct sets by (a) listing their members, (b) taking the union of other sets, or (c) using some predicate to pick out elements or subsets of some set. The starting points for this process are the empty set ∅ and the set ℕ of all natural numbers (suitably encoded as sets). If you can't construct a set in this way (like the Russell's Paradox set), odds are that it isn't a set.
These properties follow from the more useful axioms of ZFC:
- Extensionality
- Any two sets with the same members are equal.
- Existence
- ∅ is a set.
- Pairing
- For any given list of sets x, y, z, ..., { x, y, z, ... } is a set. (Strictly speaking, pairing only gives the existence of { x, y }, and the more general result requires the next axiom as well.)
- Union
- For any given set of sets { x, y, z, ... }, the set x ∪ y ∪ z ∪ ... exists.
- Power set
- For any set S, the power set ℘(S) = { A | A ⊆ S } exists.
- Specification
For any set S and any predicate P, the set { x∈S | P(x) } exists. This is called restricted comprehension. Limiting ourselves to constructing subsets of existing sets avoids Russell's Paradox, because we can't construct S = { x | x ∉ x }. Instead, we can try to construct S = { x∈T | x∉x }, but we'll find that S isn't an element of T, so it doesn't contain itself without creating a contradiction.
- Infinity
- ℕ exists, where ℕ is defined as the set containing ∅ and containing x∪{x} whenever it contains x. Here ∅ represents 0 and x∪{x} represents the successor operation. This effectively defines each number as the set of all smaller numbers, e.g. 3 = { 0, 1, 2 } = { ∅, { ∅ }, { ∅, { ∅ } } }. Without this axiom, we only get finite sets.
There are three other axioms that don't come up much in computer science:
- Foundation
Every nonempty set A contains a set B with A∩B=∅. This rather technical axiom prevents various weird sets, such as sets that contain themselves or infinite descending chains A0 ∋ A1 ∋ A2 ∋ ... .
- Replacement
- If S is a set, and R(x,y) is a predicate with the property that ∀x ∃!y R(x,y), then { y | ∃x∈S R(x,y) } is a set. Mostly used to construct astonishingly huge infinite sets.
- Choice
- For any set of nonempty sets S there is a function f that assigns to each x in S some f(x) ∈ x.
22. Cartesian products, relations, and functions
Sets are unordered: the set { a, b } is the same as the set { b, a }. Sometimes it is useful to consider ordered pairs (a, b), where we can tell which element comes first and which comes second. These can be encoded as sets using the rule (a, b) = { {a}, {a, b} }.
Given sets a and b, their Cartesian product a × b is the set { (x,y) | x ∈ a ∧ y ∈ b }, or in other words the set of all ordered pairs that can be constructed by taking the first element from a and the second from b. If a has n elements and b has m, then a × b has nm elements. For example, { 1, 2 } × { 3, 4 } = { (1,3), (1,4), (2,3), (2,4) }.
Because of the ordering, Cartesian product is not commutative in general. We usually have A×B ≠ B×A (exercise: when are they equal?).
The existence of the Cartesian product of any two sets can be proved using the axioms we already have: if (x,y) is defined as { {x}, {x,y} }, then ℘(a ∪ b) contains all the necessary sets {x} and {x,y}, and ℘℘(a ∪ b) contains all the pairs { {x}, {x,y} }. It also contains a lot of other sets we don't want, but we can get rid of them using Specification.
A subset of the Cartesian product of two sets is called a relation. An example would be the < relation on the natural numbers: { (0, 1), (0, 2), ...; (1, 2), (1, 3), ...; (2, 3), ... }. Just as sets can act like predicates of one argument (where Px corresponds to x ∈ P), relations act like predicates of two arguments. Relations are often written between their arguments, so xRy is shorthand for (x,y) ∈ R.
A special class of relations are functions. A function from a domain A to a codomain (or range) B is a relation on A and B (i.e., a subset of A × B) such that every element of A appears on the left-hand side of exactly one ordered pair. We write f: A⇒B as a short way of saying that f is a function from A to B, and for each x ∈ A write f(x) for the unique y ∈ B with (x,y) ∈ f. (Technically, knowing f alone does not tell you what the codomain is, since some elements of B may not show up at all; this can be fixed by representing a function as a pair (f,B), but it's generally not useful unless you are doing CategoryTheory.) Most of the time a function is specified by giving a rule for computing f(x), e.g. f(x) = x2.
Functions let us define sequences of arbitrary length: for example, the infinite sequence x0, x1, x2, ... of elements of some set A is represented by a function x:ℕ→A, while a shorter sequence (a0, a1, a2) would be represented by a function a:{0,1,2}→A. In both cases the subscript takes the place of a function argument: we treat xn as syntactic sugar for x(n). Finite sequences are often called tuples, and we think of the result of taking the Cartesian product of a finite number of sets A×B×C as a set of tuples (a,b,c) (even though the actual structure may be ((a,b),c) or (a,(b,c)) depending on which product operation we do first).
A function f:A→B that covers every element of B is called onto, surjective, or a surjection. If it maps distinct elements of A to distinct elements of B (i.e., if x≠y implies f(x)≠f(y)), it is called one-to-one, injective, or an injection. A function that is both surjective and injective is called a one-to-one correspondence, bijective, or a bijection. (The terms onto, one-to-one, and bijection are probably the most common, although injective and surjective are often used as well, as they avoid the confusion between one-to-one and one-to-one correspondence.) Any bijection f has an inverse f-1; this is the function { (y,x) | (x,y) ∈ f }. Two functions f:A→B and g:B→C can be composed to give a composition g∘f; g∘f is a function from A to C defined by (g∘f)(x) = g(f(x)).
Bijections let us define the size of arbitrary sets without having some special means to count elements. We say two sets A and B have the same size or cardinality if there exists a bijection f:A↔B. We can also define |A| formally as the (unique) smallest ordinal B such that there exists a bijection f:A↔B. This is exactly what we do when we do counting: to know that there are 3 stooges, we count them off 0 → Moe, 1 → Larry, 2 → Curly, giving a bijection between the set of stooges and 3 = { 0, 1, 2 }.
More on functions and relations can be found on the pages Functions and Relations.
23. Constructing the universe
With power set, Cartesian product, the notion of a sequence, etc., we can construct all of the standard objects of mathematics. For example:
- Integers
- The integers are the set ℤ = { ..., -2, -1, 0, -1, 2, ... }. We represent each integer z as an ordered pair (x,y), where x=0 ∨ y=0; formally, ℤ = { (x,y) ∈ ℕ×ℕ | x=0 ∨ y=0 }. The interpretation of (x,y) is x-y; so positive integers z are represented as (z,0) while negative integers are represented as (0,-z). It's not hard to define addition, subtraction, multiplication, etc. using this representation.
- Rationals
- The rational numbers ℚ are all fractions of the form p/q where p is an integer, q is a natural number not equal to 0, and p and q have no common factors.
- Reals
The real numbers ℝ can be defined in a number of ways, all of which turn out to be equivalent. The simplest to describe is that a real number x is represented by the set { y∈ℚ | y≤x }. Formally, we consider any subset of x of ℚ with the property y∈x ∧ z<y ⇒ z∈x to be a distinct real number (this is known as a Dedekind cut). Note that real numbers in this representation may be hard to write down.
We can also represent standard objects of computer science:
- Deterministic finite state machines
A deterministic finite state machine is a tuple (Σ,Q,q0,δ,Qaccept) where Σ is an alphabet (some finite set), Q is a state space (another finite set), q0∈Q is an initial state, δ:Q×Σ→Q is a transition function specifying which state to move to when processing some symbol in Σ, and Qaccept⊆Q is the set of accepting states. If we represent symbols and states as natural numbers, the set of all deterministic finite state machines is then just a subset of ℘ℕ×℘ℕ×ℕ×(ℕℕ×ℕ)×℘ℕ satisfying some consistency constraints.
24. Sizes and arithmetic
We can compute the size of a set by explicitly counting its elements; for example, |∅| = 0, | { Larry, Moe, Curly } | = 3, and | { x∈ℕ | x < 100 ∧ x is prime } | = 25. But sometimes it is easier to compute sizes by doing arithmetic. We can do this because many operations on sets correspond in a natural way to arithmetic operations on their sizes. (For much more on this, see HowToCount.)
Two sets A and B that have no elements in common are said to be disjoint; in set-theoretic notation, this means A∩B = ∅. In this case we have |A∪B| = |A|+|B|. The operation of disjoint union acts like addition for sets. For example, the disjoint union of 2-element set { 0, 1 } and the 3-element set { Wakko, Jakko, Dot } is the 5-element set { 0, 1, Wakko, Jakko, Dot }.
The size of a Cartesian product is obtained by multiplication: |A×B| = |A|⋅|B|. An example would be the product of the 2-element set { a, b } with the 3-element set { 0, 1, 2 }: this gives the 6-element set { (a,0), (a,1), (a,2), (b,0), (b,1), (b,2) }. Even though Cartesian product is not generally commutative, since ordinary natural number multiplication is, we always have |A×B| = |B×A|.
For power set, it is not hard to show that |℘(S)| = 2|S|. This is a special case of the size of AB, the set of all functions from B to A, which is |A||B|; for the power set we can encode P(S) using 2S, where 2 is the special set {0,1}.
24.1. Infinite sets
For infinite sets, we take the above properties as definitions of addition, multiplication, and exponentiation of their sizes. The resulting system is known as cardinal arithmetic, and the sizes that sets (finite or infinite) might have are known as cardinal numbers.
The finite cardinal numbers are just the natural numbers: 0, 1, 2, 3, ... . The first infinite cardinal number is the size of the set of natural numbers, and is written as ℵ0 ("aleph-zero," "aleph-null," or "aleph-nought"). The next infinite cardinal number is ℵ1 ("aleph-one"): it might or might not be the size of the set of real numbers, depending on whether you include the Generalized Continuum Hypothesis in your axiom system or not.
Infinite cardinals can behave very strangely. For example:
ℵ0+ℵ0=ℵ0. In other words, it is possible to have two sets A and B that both have the same size as ℕ, take their disjoint union, and get another set A+B that has the same size as ℕ. To give a specific example, let A = { 2x | x∈ℕ } and B = { 2x+1 | x∈ℕ }. These have |A|=|B|=|ℕ| because there is a bijection between each of them and ℕ built directly into their definitions. It's also not hard to see that A and B are disjoint, and A∪B = ℕ. So |A|=|B|=|A|+|B| in this case.
ℵ0⋅ℵ0=ℵ0. Example: A bijection between ℕ×ℕ and ℕ using the Cantor pairing function <x,y> = (x+y+1)(x+y)/2 + y. The first few values of this are <0,0> = 0, <1,0> = 2⋅1/2+0 = 1, <0,1> = 2⋅1/2+1 = 1, <2,0> = 3⋅2/2 + 0 = 3, <1,1> = 3⋅2/2 + 1 = 4, <0,2> = 3⋅2/2 + 2 = 5, etc. The basic idea is to order all the pairs by increasing x+y, and then order pairs with the same value of x+y by increasing y; eventually every pair is reached.
ℕ* = { all finite sequences of elements of ℕ } has size ℵ0. One way to do this to define a function recursively by setting f([]) = 0 and f([first, rest]) = 1+<first,f(rest)>, where first is the first element of the sequence and rest is all the other elements. In class, we did the example f(0,1,2) = 1+<0,f(1,2)> = 1+<0,1+<1,f(2)>> = 1+<0,1+<1,1+<2,0>>> = 1+<0,1+<1,1+3>> = 1+<0,1+<1,4>> = 1+<0,1+19> = 1+<0,20> = 1+230 = 231. This assigns a unique element of ℕ to each finite sequence, which is enough to show |ℕ*| ≤ |ℕ|; in fact, with some effort one can show that f is a bijection.
24.2. Countable sets
All of these sets have the property of being countable, which means that they can be put into a bijection with ℕ or one of its subsets. The general principle is that any sum or product of infinite cardinal numbers turns into taking the maximum of its arguments. The last case implies that anything you can write down using finitely many symbols (even if they are drawn from an infinite but countable alphabet) is countable. This has a lot of applications in computer science: one of them is that the set of all computer programs in any particular programming language is countable.
24.3. Uncountable sets
Exponentiation is different. We can easily show that 2ℵ₀ ≠ ℵ0, or equivalently that there is no bijection between ℘ℕ and ℕ. This is done using Cantor's diagonalization argument.
- Theorem
- Let S be any set. Then there is no surjection f:S→℘S.
- Proof
- Let f:S→℘S be some function from S to subsets of S. We'll construct a subset of S that f misses. Let A = { x∈S | x∉f(x) }. Suppose A = f(y). Then y∈A ↔ y∉A, a contradiction. (Exercise: Why does A exist even though the Russell's Paradox set doesn't?)
Since any bijection is also a surjection, this means that there's no bijection between S and ℘S either, implying, for example, that |ℕ| is strictly less than |℘ℕ|.
(On the other hand, it is the case that |ℕℕ| = |2ℕ|, so things are still weird up here.)
Sets that are larger than ℕ are called uncountable. A quick way to show that there is no surjection from A to B is to show that A is countable but B is uncountable. For example:
- Corollary
- There are functions f:ℕ→{0,1} that are not computed by any computer program.
- Proof
Let P be the set of all computer programs that take a natural number as input and always produce 0 or 1 as output (assume some fixed language), and for each program p ∈ P, let fp be the function that p computes. We've already argued that P is countable (each program is a finite sequence drawn from a countable alphabet), and since the set of all functions f:ℕ→{0,1} = 2ℕ has the same size as ℘ℕ, it's uncountable. So some f gets missed: there is at least one function from ℕ to {0,1} that is not equal to fp for any program p.
The fact that there are more functions from ℕ to ℕ than there are elements of ℕ is one of the reasons why set theory (slogan: "everything is a set") beat out lambda calculus (slogan: "everything is a function from functions to functions") in the battle over the foundations of mathematics. And this is why we do set theory in CS202 and lambda calculus gets put in CS201.
25. Further reading
See RosenBook §§2.1–2.2, BiggsBook Chapter 2, or Naive set theory.
26. NaturalNumbers
The natural numbers are the set ℕ = { 0, 1, 2, 3, .... }. These correspond to all possible sizes of finite sets; in a sense, the natural numbers are precisely those numbers that occur in nature: one can have a field with 0, 1, 2, 3, etc. sheep in it, but it's hard to have a field with -12 or 22/7 sheep in it.
Warning: While this is definition of ℕ is almost universally used in computer science, and is used in RosenBook, some mathematicians—including the author of BiggsBook—leave zero out of the natural numbers. There are several possible reasons why you might do this:
- You were born well before the invention of zero approximately two millenia back by the ancient Indians, Babylonians, and/or Mayans.
- You were taught by extremely conservative schoolmasters who still hadn't got a handle on this newfangled zero thing.
- You live in a country that is so rich in sheep that the thought of a field with no sheep in it seems unnatural.
- You are a number theorist, and you don't want to have follow "Let n be a natural number..." with "(except zero)" in every theorem you write.
My suspicion is that Biggs falls into the last category (and might fall into some of the earlier ones). For the purposes of CS202 we will adopt the usual convention in ComputerScience and start the naturals at zero. However, you should keep an eye out for assumptions that the natural numbers don't include zero. The terms positive integers (for {1, 2, 3, ...}) and non-negative integers (for {0, 1, 2, 3, ...}) can also be helpful for avoiding confusion.
27. Axioms
There are several different ways to define the naturals. That these definitions all yield the same object is one of the reasons why they are so natural.
27.1. Peano axioms
The PeanoAxioms define the natural numbers directly from logic. It is not hard to show that the usual natural numbers satisfy these axioms (whether or not you throw out zero). Unfortunately, the Peano axioms by themselves don't give us many of the usual operations (like addition and multiplication) that we expect to be able to do to numbers.
27.2. Set-theoretic definition
In SetTheory, a natural number is defined as a finite1 set x such that (a) every element y of x is also a subset of x, and (b) every element y of x is also a natural number. The existence of the set of natural numbers is asserted by the Axiom of Infinity. The smallest natural number is the empty set, which we take as representing 0. Next is 1 = { 0 }, 2 = { 0, 1 }, 3 = { 0, 1, 2 }, etc. It can easily be verified that each natural number defined in this way is indeed a subset of the next. It's not hard to show that these set-theoretic natural numbers satisfy the Peano axioms, and it's possible to define addition and multiplication operations on them that satisfy the arithmetic and order axioms below (we'll see more of this in HowToCount). Ordering is by inclusion: for the set-theoretic definition, n < m just in case n is an element of m.
27.3. Arithmetic and order axioms
Axioms for arithmetic in ℕ-{0} are given in Section 4.1 of BiggsBook. RosenBook doesn't spend much time on axiomatizing the naturals, relying instead on the deep intuition about natural numbers that most of us had trained into us from early childhood.
You've probably already seen all of the usual axioms early in your mathematical education, with the possible exception of mz = nz implies m = n. Note that unlike the other axioms, this one does not extend to ℕ, since m⋅0 = n⋅0 = 0 for any m and n. An extended list of axioms for ℕ including zero might look like
- a+b is in ℕ. [Closure under addition]
- a⋅b is in ℕ. [Closure under multiplication]
- a+b = b+a. [Commutativity of addition]
- (a+b)+c = a+(b+c). [Associativity of addition]
- ab = ba. [Commutativity of multiplication]
- (ab)c = a(bc). [Associativity of multiplication]
- There is an element 1 of ℕ such that n1 = n for all n. [Multiplicative identity]
- mz = nz implies m = n when z ≠ 0 (see below for 0). [Multiplicative cancellation]
- a(b+c) = ab+ac. [Distributivity of multiplication over addition]
For any m and n, exactly one of n < m, n = m, or n > m is true. [Trichotomy]
- There is an element 0 of ℕ such that n+0 = n for all n. [Additive identity]
- 0a = 0. [Multiplicative annihilator]
The numbering follows BiggsBook, except for the last two axioms, which don't appear in BiggsBook outside of Exercise 4.1.3.
Note that < is defined in terms of +. In our terms, n < m means that there exists some x such that x is not equal to 0 and n+x = m.
One problem with these axioms (as compared to the Peano axioms) is that they are not very restrictive: they work equally well for e.g. the non-negative reals or the non-negative rationals, and extend to all of the reals or the rationals if we adjust the definition of <. So the arithmetic axioms can't be used as a definition of the naturals, even though they are much more convenient for doing actual arithmetic than the more basic definitions.
Much of the work in logic in the early 20th century involved showing that addition, multiplication, etc. could be defined in terms of much more primitive operations like successor, and that the operations so defined behaved the way we'd expect. This program was not always popular with non-logicians: as Henri_Poincaré put it (quoted in Bell and Machover's A Course in Mathematical Logic, North-Holland, 1977): "On the contrary, I find nothing in logistic for the discoverer but shackles. It does not help us at all in the direction of conciseness, far from it: and if it requires 27 equations to establish that 1 is a number, how many will it requires to demonstrate a real theorem?" Thankfully, we get to build on these efforts, and can treat the arithmetic axioms as our own convenient library of lemmas rather than having to reach down into the raw logical swamps.
27.3.1. Formal definition of arithmetic operations in terms of successor
Here's a formal definition of + in terms of successor:
- ∀x 0+x = x.
- ∀x ∀y Sx+y = x+Sy.
This defines the sum of two natural numbers uniquely because we can use the second rule to move all the S's off of the first addend onto the second one, until we get down to zero (recall that under the PeanoAxioms a natural number like 37 is really just a convenient shorthand for SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS0).
Here's multiplication:
- ∀x 0x = 0.
- ∀x ∀y (Sx)y = xy + y.
With the above rules for addition, this lets us multiply any two numbers very slowly: SS0⋅SS0 = (S0⋅SS0) + SS0 = ((0⋅SS0) + SS0) + SS0 = (0 + SS0) + SS0 = SS0 + SS0 = S0 + SSS0 = 0 + SSSS0 = SSSS0. Normal people write this as 2⋅2 = 4 and skip all the S's.
Here's <:
x < y ⇔ ∃z (z ≠ 0 ∧ x+z = y).
Note that this fails badly if z ranges over a larger set, like the integers.
With enough time on your hands, it is in principle possible to prove all of the arithmetic axioms given earlier hold for these definitions of +, ⋅, and <.
28. Order properties
The < relation is a total order (see Relations). This means that in addition to trichotomy, transitivity holds: a < b and b < c implies a < c. Transitivity can be proved from the definition of < and axioms 1-12; see Exercise 4.2.1 in BiggsBook.
However, < is even stronger than this: it is also a well order. This means that any subset of the natural numbers has a least element, which is the key to carrying out InductionProofs.
29. PeanoAxioms
30. InductionProofs
31. Simple induction
Most of the ProofTechniques we've talked about so far are only really useful for proving a property of a single object (although we can sometimes use generalization to show that the same property is true of all objects in some set if we weren't too picky about which single object we started with). Mathematical induction (which mathematicians just call induction) is a powerful technique for showing that some property is true for many objects, where you can use the fact that it is true for small objects as part of the proof that it is true for large objects.
The basic framework for induction is as follows: given a sequence of statements P(0), P(1), P(2), we'll prove that P(0) is true (the base case), and then prove that for all k, P(k) ⇒ P(k+1) (the induction step). We then conclude that P(n) is in fact true for all n.
31.1. Why induction works
There are three ways to show that induction works, depending on where you got your natural numbers from.
- Peano axioms
If you start with the PeanoAxioms, induction is one of them. Nothing more needs to be said.
- Well-ordering of the naturals
A set is well-ordered if every subset has a smallest element. (An example of a set that is not well-ordered is the integers ℤ.) If you build the natural numbers using 0 = { } and x+1 = x ∪ {x}, it is possible to prove that the resulting set is well-ordered. Because it is well-ordered, if P(n) does not hold for all n, there is a smallest n for which P(n) is false. But then either this n = 0, contradicting the base case, or P(n-1) is true (because otherwise n would not be the smallest) and P(n) is false, contradicting the induction step.
- Method of infinite descent
The original version, due to Fermat, goes like this: Suppose P(n) is false for some n > 0. Since P(n-1) ⇒ P(n) is logically equivalent to ¬P(n) ⇒ ¬P(n-1), we can conclude (using the induction step) ¬P(n-1). Repeat until you reach 0. The problem with this version is that the "repeat" step is in effect using an induction argument. The modern solution to this problem is to recast the argument to look like the well-ordering argument above, by assuming that n is the smallest n for which P(n) is false and asserting a contradiction once you prove ¬P(n-1). Historical note: Fermat may have used this technique to construct a plausible but invalid proof of his famous "Last Theorem" that an+bn=cn has no non-trivial integer solutions for n > 2.
31.2. Examples
The PigeonholePrinciple.
The number of subsets of an n-element set is 2n.
1+3+5+7+...+(2n+1) = (n+1)2.
2n > n2 for n ≥ 5.
32. Strong induction
Sometimes when proving that the induction hypothesis holds for n+1, it helps to use the fact that it holds for all n' < n+1, not just for n. This sort of argument is called strong induction. Formally, it's equivalent to simple induction: the only difference is that instead of proving ∀k P(k) ⇒ P(k+1), we prove ∀k (∀m≤k Q(m)) ⇒ Q(k+1). But this is exactly the same thing if we let P(k) ≡ ∀m≤k Q(m), since if ∀m≤k Q(m) implies Q(k+1), it also implies ∀m≤k+1 Q(m), giving us the original induction formula ∀k P(k) ⇒ P(k+1).
32.1. Examples
Every n > 1 can be factored into a product of one or more prime numbers. Proof: By induction on n. The base case is n = 2, which factors as 2 = 2 (one prime factor). For n > 2, either (a) n is prime itself, in which case n = n is a prime factorization; or (b) n is not prime, in which case n = ab for some a and b, both greater than 1. Since a and b are both less than n, by the induction hypothesis we have a = p1p2...pk for some sequence of one or more primes and similarly b = p'1p'2...p'k'. Then n = p1p2...pkp'1p'2...p'k' is a prime factorization of n.
Every deterministic bounded two-player perfect-information game that can't end in a draw has a winning strategy for one of the players. A perfect-information game is one in which both players know the entire state of the game at each decision point (like Chess or Go, but unlike Poker or Bridge); it is deterministic if there is no randomness that affects the outcome (this excludes Backgammon and Monopoly, some variants of Poker, and multiple hands of Bridge), and it's bounded if the game is guaranteed to end in at most a fixed number of moves starting from any reachable position (this also excludes Backgammon and Monopoly). Proof: For each position x, let b(x) be the bound on the number of moves made starting from x. Then if y is some position reached from x in one move, we have b(y) < b(x) (because we just used up a move). Let f(x) = 1 if the first player wins starting from position x and f(x) = 0 otherwise. We claim that f is well-defined. Proof: If b(x) = 0, the game is over, and so f(x) is either 0 or 1, depending on who just won. If b(x) > 0, then f(x) = max { f(y) | y is a successor to x } if it's the first player's turn to move and f(x) = min { f(y) | y is a successor to x } if it's the second player's turn to move. In either case each f(y) is well-defined (by the induction hypothesis) and so f(x) is also well-defined.
The DivisionAlgorithm: for each n,m ∈ ℕ there is a unique q∈ℕ and a unique r∈ℕ such that n = qm+r and0≤r<m. Proof: Fix m then proceed by induction on n. If n < m, then if q > 0 we have n = qm+r ≥ 1⋅m ≥ m, a contradiction. So in this case q = 0 is the only solution, and since n = qm + r = r we have a unique choice of r = n. If n ≥ m, by the induction hypothesis there is a unique q' and r' such that n-m = q'm+r' where 0≤r'<m. But then q = q'+1 and r = r' satisfies qm+r = (q'-1+1)m+r = (q'm+r') + m = (n-m) + m = n. To show that this solution is unique, if there is some other q'' and r'' such that q''m+r'' = n, then (q''-1)m + r'' = n-m = q'm+r', and by the uniqueness of q' and r' (ind. hyp. again), we have q''-1 = q' = q-1 and r'' = r' = r, giving that q'' = q and r'' = r. So q and r are unique.
33. Recursion
A definition with the structure of an inductive proof (give a base case and a rule for building bigger structures from smaller ones) Structures defined in this way are recursively-defined.
Examples of recursively-defined structures:
- Finite Von Neumann ordinals
- A finite von Neumann ordinal is either (a) the empty set ∅, or (b) x ∪ { x }, where x is a finite von Neumann ordinal.
- Complete binary trees
A complete binary tree consists of either (a) a leaf node, or (b) an internal node (the root) with two complete binary trees as children (or subtrees).
- Boolean formulas
- A boolean formula consists of either (a) a variable, (b) the negation operator applied to a Boolean formula, (c) the AND of two Boolean formulas, or (d) the OR of two Boolean formulas. A monotone Boolean formula is defined similarly, except that negations are forbidden.
- Finite sequences, recursive version
Before we defined a finite sequence as a function from some natural number (in its set form: n = { 0, 1, 2, ..., n-1 }) to some range. We could also define a finite sequence over some set S recursively, by the rule: [ ] (the empty sequence) is a finite sequence, and if a is a finite sequence and x∈S, then (x,a) is a finite sequence. (Fans of LISP will recognize this method immediately.)
Key point is that in each case the definition of an object is recursive---the object itself may appear as part of a larger object. Usually we assume that this recursion eventually bottoms out: there are some base cases (e.g. leaves of complete binary trees or variables in Boolean formulas) that do not lead to further recursion. If a definition doesn't bottom out in this way, the class of structures it describes might not be well-defined (i.e., we can't tell if some structure is an element of the class or not).
33.1. Recursively-defined functions
We can also define functions on recursive structures recursively:
- The depth of a binary tree
For a leaf, 0. For a tree consisting of a root with two subtrees, 1+max(d1, d2), where d1 and d2 are the depths of the two subtrees.
- The value of a Boolean formula given a particular variable assignment
- For a variable, the value (true or false) assigned to that variable. For a negation, the negation of the value of its argument. For an AND or OR, the AND or OR of the values of its arguments. (This definition is not quite as trivial as it looks, but it's still pretty trivial.)
Or we can define ordinary functions recursively:
- The Fibonacci series
Let F(0) = F(1) = 1. For n > 1, let F(n) = F(n-1) + F(n-2).
- Factorial
Let 0! = 1. For n > 0, let n! = n × (n-1)!.
33.2. Recursive definitions and induction
Recursive definitions have the same form as an induction proof. There are one or more base cases, and one or more recursion steps that correspond to the induction step in an induction proof. The connection is not surprising if you think of a definition of some class of objects as a predicate that identifies members of the class: a recursive definition is just a formula for writing induction proofs that say that certain objects are members.
Recursively-defined objects and functions also lend themselves easily to induction proofs about their properties; on general structures, such induction arguments go by the name of structural induction.
34. Structural induction
For finite structures, we can do induction over the structure. Formally we can think of this as doing induction on the size of the structure or part of the structure we are looking at.
Examples:
- Every complete binary tree with n leaves has n-1 internal nodes
Base case is a tree consisting of just a leaf; here n = 1 and there are n - 1 = 0 internal nodes. The induction step considers a tree consisting of a root and two subtrees. Let n1 and n2 be the number of leaves in the two subtrees; we have n1+n2 = n; and the number of internal nodes, counting the nodes in the two subtrees plus one more for the root, is (n1-1)+(n2-1)+1 = n1+n2 - 1 = n-1.
- Monotone Boolean formulas generate monotone functions
- What this means is that changing a variable from false to true can never change the value of the formula from true to false. Proof is by induction on the structure of the formula: for a naked variable, it's immediate. For an AND or OR, observe that changing a variable from false to true can only leave the values of the arguments unchanged, or change one or both from false to true (induction hypothesis); the rest follows by staring carefully at the truth table for AND or OR.
- Bounding the size of a binary tree with depth d
We'll show that it has at most 2d+1-1 nodes. Base case: the tree consists of one leaf, d = 0, and there are 20+1-1 = 2-1 = 1 nodes. Induction step: Given a tree of depth d > 1, it consists of a root (1 node), plus two subtrees of depth at most d-1. The two subtrees each have at most 2d-1+1-1 = 2d-1 nodes (induction hypothesis), so the total number of nodes is at most 2(2d-1)+1 = 2d+1+2-1 = 2d+1-1.
35. SummationNotation
36. Summations
Summations are the discrete versions of integrals; given a sequence xa, xa+1, ..., xb, its sum xa + xa+1 + ... + xb is written as

The large jagged symbol is a stretched-out version of a capital Greek letter sigma. The variable i is called the index of summation, a is the lower bound or lower limit, and b is the upper bound or upper limit. Mathematicians invented this notation centuries ago because they didn't have for loops; the intent is that you loop through all values of i from a to b (including both endpoints), summing up the argument of the ∑ for each i.
If b < a, then the sum is zero. For example,
![\[\sum_{i=0}^{-5} \frac{2^i \sin i}{i^3} = 0.\] \[\sum_{i=0}^{-5} \frac{2^i \sin i}{i^3} = 0.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_2982216f15a5c4641c2b0dc7deb0cfc78ca67dbc_p1.png)
This rule mostly shows up as an extreme case of a more general formula, e.g.
![\[\sum_{i=1}^{n} i = \frac{n(n+1)}{2},\] \[\sum_{i=1}^{n} i = \frac{n(n+1)}{2},\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_331516ba008cdd1c6b1cca4d32fcabcbe558fad5_p1.png)
which still works even when n=0 or n=-1 (but not for n=-2).
Summation notation is used both for laziness (it's more compact to write

than 1 + 3 + 5 + 7 + ... + (2n+1)) and precision (it's also more clear exactly what you mean).
36.1. Formal definition
For finite sums, we can formally define the value by either of two recurrences:

In English, we can compute a sum recursively by computing either the sum of the last n-1 values or the first n-1 values, and then adding in the value we left out. (For infinite sums we need a different definition; see below.)
36.2. Choosing and replacing index variables
When writing a summation, you can generally pick any index variable you like, although i, j, k, etc. are popular choices. Usually it's a good idea to pick an index that isn't used outside the sum. Though
![\[\sum_{n=0}^{n} n = \sum_{i=0}^{n} i\] \[\sum_{n=0}^{n} n = \sum_{i=0}^{n} i\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_434cd307ef49c57326bc756589bdf1a34bb51330_p1.png)
has a well-defined meaning, the version on the right-hand side is a lot less confusing.
In addition to renaming indices, you can also shift them, provided you shift the bounds to match. For example, rewriting
![\[\sum_{i=1}^{n} (i-1)\] \[\sum_{i=1}^{n} (i-1)\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_84a640fc331a8175961ab921e43b3435d62627c6_p1.png)
as
![\[\sum_{j=0}^{n-1} j\] \[\sum_{j=0}^{n-1} j\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_a180da0847e1959f92c9074e78c48a33b34bcdec_p1.png)
(by substituting j for i-1) makes the sum more convenient to work with.
36.3. Scope
The scope of a summation extends to the first addition or subtraction symbol that is not enclosed in parentheses or part of some larger term (e.g., in the numerator of a fraction). So
![\[\sum_{i=1}^{n} i^2 + 1 = \left(\sum_{i=1}^{n} i^2\right) + 1 = 1 + \sum_{i=1}^{n} i^2 \ne \sum_{i=1}^{n} (i^2+1).\] \[\sum_{i=1}^{n} i^2 + 1 = \left(\sum_{i=1}^{n} i^2\right) + 1 = 1 + \sum_{i=1}^{n} i^2 \ne \sum_{i=1}^{n} (i^2+1).\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_5b2128246043ac3fc3ed1297f06c555e6fbfb24a_p1.png)
Since this can be confusing, it is generally safest to wrap the sum in parentheses (as in the second form) or move any trailing terms to the beginning. An exception is when adding together two sums, as in
![\[\sum_{i=1}^{n} i^2 + \sum_{i=1}^{n^2} i = \left(\sum_{i=1}^{n} i^2\right) + \left(\sum_{i=1}^{n^2} i\right).\] \[\sum_{i=1}^{n} i^2 + \sum_{i=1}^{n^2} i = \left(\sum_{i=1}^{n} i^2\right) + \left(\sum_{i=1}^{n^2} i\right).\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_28d6ed7e4b8dd3d74601035f0de9f03173374412_p1.png)
Here the looming bulk of the second Sigma warns the reader that the first sum is ending; it is much harder to miss than the relatively tiny plus symbol in the first example.
36.4. Sums over given index sets
Sometimes we'd like to sum an expression over values that aren't consecutive integers, or may not even be integers at all. This can be done using a sum over all indices that are members of a given index set, or in the most general form satisfy some given predicate (with the usual set-theoretic caveat that the objects that satisfy the predicate must form a set). Such a sum is written by replacing the lower and upper limits with a single subscript that gives the predicate that the indices must obey.
For example, we could sum i2 for i in the set {3,5,7}:
![\[\sum_{i \in \{3,5,7\}} i^2 = 3^2 + 5^2 + 7^2 = 83.\] \[\sum_{i \in \{3,5,7\}} i^2 = 3^2 + 5^2 + 7^2 = 83.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_2656ef5af11c0abdc3e51e6ab5fcb82b61adab83_p1.png)
Or we could sum the sizes of all subsets of a given set S:
![\[\sum_{A \subseteq S} |A|.\] \[\sum_{A \subseteq S} |A|.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_fda638ea6fb3b686e2379f4e4fd4e5aa50280c0a_p1.png)
Or we could sum the inverses of all prime numbers less than 1000:
![\[\sum_{\mbox{\scriptsize $p < 1000$, $p$ is prime}} 1/p.\] \[\sum_{\mbox{\scriptsize $p < 1000$, $p$ is prime}} 1/p.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_4a4a15d96d318af055367b45e7d08648fae2ff44_p1.png)
Sometimes when writing a sum in this form it can be confusing exactly which variable or variables are the indices. The usual convention is that a variable is always an index if it doesn't have any meaning outside the sum, and if possible the index variable is put first in the expression under the Sigma if possible. If it is not obvious what a complicated sum means, it is generally best to try to rewrite it to make it more clear; still, you may see sums that look like
![\[\sum_{1 \le i < j \le n} \frac{i}{j}\] \[\sum_{1 \le i < j \le n} \frac{i}{j}\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_6f3c8dc6a140fc7cb631ba4bc9ea3cfe740d0a87_p1.png)
or
![\[\sum_{x \in A \subseteq S} |A|\] \[\sum_{x \in A \subseteq S} |A|\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_29eb73084e8e57b281aa85e29d6fb2b2cdf121df_p1.png)
where the first sum sums over all pairs of values (i,j) that satisfy the predicate, with each pair appearing exactly once, and the second sums over all sets A that are subsets of S and contain x (assuming x and S are defined outside the summation). Hopefully, you will not run into too many sums that look like this, but it's worth being able to decode them if you do.
Sums over a given set are guaranteed to be well-defined only if the set is finite. In this case we can use the fact that there is a bijection between any finite set S and the ordinal |S| to rewrite the sum as a sum over indices in |S|. For example, if |S| = n, then there exists a bijection f:{0..n-1}↔S, so we can define
![\[\sum_{i \in S} x_i = \sum_{i=0}^{n-1} x_{f(i)}.\] \[\sum_{i \in S} x_i = \sum_{i=0}^{n-1} x_{f(i)}.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_11a8f6cd8863463c88ffd7bf300f4db7879fbdc5_p1.png)
If S is infinite, this is trickier. For countable S, where there is a bijection f:ℕ↔S, we can sometimes rewrite
![\[\sum_{i \in S} x_i = \sum_{i=0}^{\infty} x_{f(i)}.\] \[\sum_{i \in S} x_i = \sum_{i=0}^{\infty} x_{f(i)}.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_d7694f037c0d52432bb74e6372530e59cc527f6d_p1.png)
and use the definition of an infinite sum (given below). Note that if the xi have different signs the result we get may depend on which bijection we choose. For this reason such infinite sums are probably best avoided unless you can explicitly use ℕ as the index set.
36.5. Sums without explicit bounds
When the index set is understood from context, it is often dropped, leaving only the index, as in ∑i i2. This will generally happen only if the index spans all possible values in some obvious range, and can be a mark of sloppiness in formal mathematical writing. Theoretical physicists adopt a still more lazy approach, and leave out the ∑i part entirely in certain special types of sums: this is known as the Einstein summation convention after the notoriously lazy physicist who proposed it.
36.6. Infinite sums
Sometimes you may see an expression where the upper limit is infinite, as in
![\[\sum_{i=0}^{\infty} \frac{1}{i^2}.\] \[\sum_{i=0}^{\infty} \frac{1}{i^2}.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_c6e3cf4b87ee8cd067da7db6d64efb9d63337ee5_p1.png)
The meaning of this expression is the limit of the series s obtained by taking the sum of the first term, the sum of the first two terms, the sum of the first three terms, etc. The limit converges to a particular value x if for any ε>0, there exists an N such that for all n > N, the value of sn is within ε of x (formally, |sn-x| < ε). We will see some examples of infinite sums when we look at GeneratingFunctions.
36.7. Double sums
Nothing says that the expression inside a summation can't be another summation. This gives double sums, such as in this rather painful definition of multiplication for non-negative integers:
![\[a \times b \stackrel{\mbox{\scriptsize def}}{=} \sum_{i=1}^{a} \sum_{j=1}^{b} 1.\] \[a \times b \stackrel{\mbox{\scriptsize def}}{=} \sum_{i=1}^{a} \sum_{j=1}^{b} 1.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_3b244240fff199363ecac4094e04e9216ed1f1a8_p1.png)
If you think of a sum as a for loop, a double sum is two nested for loops. The effect is to sum the innermost expression over all pairs of values of the two indices.
Here's a more complicated double sum where the limits on the inner sum depend on the index of the outer sum:
![\[\sum_{i=0}^{n} \sum_{j=0}^{i} (i+1)(j+1).\] \[\sum_{i=0}^{n} \sum_{j=0}^{i} (i+1)(j+1).\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_a425a2c80524bb1553416412660a04d047963edd_p1.png)
When n=1, this will compute (0+1)(0+1) + (1+1)(0+1) + (1+1)(1+1) = 7. For larger n the number of terms grows quickly.
There are also triple sums, quadruple sums, etc.
37. Computing sums
When confronted with some nasty sum, it is nice to be able to convert into a simpler expression that doesn't contain any Sigmas. It is not always possible to do this, and the problem of finding a simpler expression for a sum is very similar to the problem of computing an integral (see HowToIntegrate): in both cases the techniques available are mostly limited to massaging the summation until it turns into something whose simpler expression you remember. To do this, it helps to both (a) have a big toolbox of sums with known values, and (b) have some rules for manipulating summations to get them into a more convenient form. We'll start with the toolbox.
37.1. Some standard sums
Here are the three formula you should either memorize or remember how to derive:

Rigorous proofs of these can be obtained by induction on n.
For not so rigorous proofs, the second identity can be shown (using a trick alleged to have been invented by the legendary 18th-century mathematician Carl_Friedrich_Gauss at a frighteningly early age; see here for more details on this legend) by adding up two copies of the sequence running in opposite directions, one term at a time:
S = 1 + 2 + 3 + .... + n S = n + n-1 + n-2 + .... + 1 ------------------------------------------------------ 2S = (n+1) + (n+1) + (n+1) + .... + (n+1) = n(n+1),
and from 2S=n(n+1) we get S = n(n+1)/2.
For the last identity, start with
![\[\sum_{i=0}^{\infty} r^i = \frac{1}{1-r},\] \[\sum_{i=0}^{\infty} r^i = \frac{1}{1-r},\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_57b487bbab22927814b613c2e588aaaf626bd560_p1.png)
which holds when |r| < 1. The proof is that if
![\[S = \sum_{i=0}^{\infty} r^i\] \[S = \sum_{i=0}^{\infty} r^i\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_89eb60890414027cf75c0717e8cff17499c72afd_p1.png)
then
![\[rS = \sum_{i=0}^{\infty} r^{i+1} = \sum_{i=1}^{\infty} r^i\] \[rS = \sum_{i=0}^{\infty} r^{i+1} = \sum_{i=1}^{\infty} r^i\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_b4dd58b434d59f2febc967aea39406f66438da56_p1.png)
and so
![\[S-rS = r^0 = 1.\] \[S-rS = r^0 = 1.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_db76d66d4ad405c6dcaff85c9705d6c89a7589c0_p1.png)
Solving for S then gives S = 1/(1-r).
We can now get the sum up to n by subtracting off the extra terms starting with rn+1:
![\[\sum_{i=0}^{n} r^i = \sum_{i=0}^{\infty} r^i - r^{n+1} \sum_{i=0}^{\infty} r^i = \frac{1}{1-r} - \frac{r^{n+1}}{1-r} = \frac{1-r^{n+1}}{1-r}.\] \[\sum_{i=0}^{n} r^i = \sum_{i=0}^{\infty} r^i - r^{n+1} \sum_{i=0}^{\infty} r^i = \frac{1}{1-r} - \frac{r^{n+1}}{1-r} = \frac{1-r^{n+1}}{1-r}.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_c320cba1f5204b5396b2eba8deee6bc8a6b17985_p1.png)
Amazingly enough, this formula works even when r is greater than 1. If r is equal to 1, then the formula doesn't work (it requires dividing zero by zero), but there is an easier way to get the solution.
Other useful sums can be found in various places. RosenBook and ConcreteMathematics both provide tables of sums in their chapters on GeneratingFunctions. But it is usually better to be able to reconstruct the solution of a sum rather than trying to memorize such tables.
37.2. Summation identities
The summation operator is linear. This means that constant factors can be pulled out of sums:
![\[\sum_{i \in S} a x_i = a \sum_{i \in S} x_i\] \[\sum_{i \in S} a x_i = a \sum_{i \in S} x_i\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_085bada7dc9472d29e1c2056dc9992e45d4f65cb_p1.png)
and sums inside sums can be split:
![\[\sum_{i \in S} (x_i + y_i) = \sum_{i \in S} x_i + \sum_{i \in S} y_i.\] \[\sum_{i \in S} (x_i + y_i) = \sum_{i \in S} x_i + \sum_{i \in S} y_i.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_e462b830280a2e74c41a463ce9866919f2a9775d_p1.png)
With multiple sums, the order of summation is not important, provided the bounds on the inner sum don't depend on the index of the outer sum:
![\[\sum_{i \in S} \sum_{j \in T} x_{ij} = \sum_{j \in T} \sum_{i \in S} x_{ij}.\] \[\sum_{i \in S} \sum_{j \in T} x_{ij} = \sum_{j \in T} \sum_{i \in S} x_{ij}.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_fbf0625abef756a58c3bf4c585753c3a96bcf543_p1.png)
Products of sums can be turned into double sums of products and vice versa:
![\[\left(\sum_{i \in S} x_i\right)\left(\sum_{j \in T} y_j\right)
= \sum_{i \in S} \sum_{j \in T} x_i y_j.\] \[\left(\sum_{i \in S} x_i\right)\left(\sum_{j \in T} y_j\right)
= \sum_{i \in S} \sum_{j \in T} x_i y_j.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_996ead404602e11795dcc1ed817e0298e5d51303_p1.png)
These identities can often be used to transform a sum you can't solve into something simpler.
37.3. What to do if nothing else works
If nothing else works, you can try using the guess but verify method, which is a variant on the same method for identifying sequences. Here we write out the values of the sum for the first few values of the upper limit (for example), and hope that we recognize the sequence. If we do, we can then try to prove that a formula for the sequence of sums is correct by induction.
Example: Suppose we want to compute
![\[
S(n) = \sum_{k=1}^{n} (2k-1)
\] \[
S(n) = \sum_{k=1}^{n} (2k-1)
\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_ee8c69f7ecb0c67ac3fb18f1c3c74476b0b9e8f2_p1.png)
but that it doesn't occur to us to split it up and use the ∑k and ∑1 formulas. Instead, we can write down a table of values:
n |
S(n) |
0 |
0 |
1 |
1 |
2 |
1+3=4 |
3 |
1+3+5=9 |
4 |
1+3+5+7=16 |
5 |
1+3+5+7+9=25 |
At this point we might guess that S(n) = n2. To verify this, observe that it holds for n=0, and for larger n we have S(n) = S(n-1) + (2n-1) = (n-1)2 + 2n - 1 = n2 - 2n + 1 - 2n - 1 = n2. So we can conclude that our guess was correct.
If this doesn't work, you could always try using GeneratingFunctions.
37.4. Strategies for asymptotic estimates
Mostly in AlgorithmAnalysis we do not need to compute sums exactly, because we are just going to wrap the result up in some asymptotic expression anyway (see AsymptoticNotation). This makes our life much easier, because we only need an approximate solution.
Here's my general strategy for computing sums:
37.4.1. Pull out constant factors
Pull as many constant factors out as you can (where constant in this case means anything that does not involve the summation index). Example:

37.4.2. Bound using a known sum
See if it's bounded above or below by some other sum whose solution you already know. Good sums to try (you should memorize all of these):
37.4.2.1. Geometric series

The way to recognize a geometric series is that the ratio between adjacent terms is constant. If you memorize the second formula, you can rederive the first one. If you're Carl_Friedrich_Gauss, you can skip memorizing the second formula.
A useful trick to remember for geometric series is that if x is a constant that is not exactly 1, the sum is always big-Theta of its largest term. So for example

(the exact value is 2n+1-2), and

(the exact value is 1-2-n). This fact is the basis of the Master Theorem, described in SolvingRecurrences. If the ratio between terms equals 1, the formula doesn't work; instead, we have a constant series (see below).
37.4.2.2. Constant series

37.4.2.3. Arithmetic series
The simplest arithmetic series is

The way to remember this formula is that it's just n times the average value (n+1)/2. The way to recognize an arithmetic series is that the difference between adjacent terms is constant. The general arithmetic series is of the form

Because the general series expands so easily to the simplest series, it's usually not worth memorizing the general formula.
37.4.2.4. Harmonic series

Can be rederived using the integral technique given below or by summing the last half of the series, so this is mostly useful to remember in case you run across Hn (the n-th harmonic number).
37.4.3. Bound part of the sum
See if there's some part of the sum that you can bound. For example,

has a (painful) exact solution, or can be approximated by the integral trick described below, but it can very quickly be solved to within a constant factor by observing that

and

37.4.4. Integrate
Integrate. If f(n) is non-decreasing and you know how to integrate it, then

which is enough to get a big-Theta bound for almost all functions you are likely to encounter in algorithm analysis. If you don't remember how to integrate, see HowToIntegrate.
37.4.5. Grouping terms
Try grouping terms together. For example, the standard trick for showing that the harmonic series is unbounded in the limit is to argue that 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... ≥ 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + ... ≥ 1 + 1/2 + 1/2 + 1/2 + ... . I usually try everything else first, but sometimes this works if you get stuck.
37.4.6. Oddities
One oddball sum that shows up occasionally but is hard to solve using any of the above techniques is

If a < 1, this is Θ(1) (the exact formula for

when a < 1 is a/(1-a)2, which gives a constant upper bound for the sum stopping at n); if a = 1, it's just an arithmetic series; if a > 1, the largest term dominates and the sum is Θ(ann) (there is an exact formula, but it's ugly—if you just want to show it's O(ann), the simplest approach is to bound the series

by the geometric series

I wouldn't bother memorizing this one provided you bookmark this page.
37.4.7. Final notes
In practice, almost every sum you are likely to encounter in AlgorithmAnalysis will be of the form

where f(n) is exponential (so that it's bounded by a geometric series and the largest term dominates) or polynomial (so that f(n/2) = Θ(f(n)) and the sum is Θ(n f(n)) using the

lower bound).
ConcreteMathematics spends a lot of time on computing sums exactly. The most useful technique for doing this is to use GeneratingFunctions.
38. Products
What if you want to multiple a series of values instead of add them? The notation is the same as for a sum, except that you replace the Sigma with a Pi, as in this definition of the factorial function for non-negative n.
![\[n! \stackrel{\mbox{\scriptsize def}}{=} \prod_{i=1}^{n} i = 1 \cdot 2 \cdot \cdots \cdot n.\] \[n! \stackrel{\mbox{\scriptsize def}}{=} \prod_{i=1}^{n} i = 1 \cdot 2 \cdot \cdots \cdot n.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_1d385826ca3bffff43fbe9476e1ca312ba42dc05_p1.png)
The other difference is that while an empty sum is defined to have the value 0, an empty product is defined to have the value 1. The reason for this rule (in both cases) is that an empty sum or product should return the identity element for the corresponding operation—the value that when added to or multiplied by some other value x doesn't change x. This allows writing general rules like:

which holds as long as A∩B=Ø. Without the rule that the sum of an empty set was 0 and the product 1, we'd have to put in a special case for when one or both of A and B were empty.
Note that a consequence of this definition is that 0! = 1.
39. Other big operators
Some more obscure operators also allow you to compute some aggregate over a series, with the same rules for indices, lower and upper limits, etc., as ∑ and ∏. These include:
- Big AND:
![\[\bigwedge_{x \in S} P(x) \equiv P(x_1) \wedge P(x_2) \wedge \ldots \equiv \forall x \in S: P(x).\] \[\bigwedge_{x \in S} P(x) \equiv P(x_1) \wedge P(x_2) \wedge \ldots \equiv \forall x \in S: P(x).\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_e6651e2ab4896d7727685173d160c98d9fdb8ca2_p1.png)
- Big OR:
![\[\bigvee_{x \in S} P(x) \equiv P(x_1) \vee P(x_2) \vee \ldots \equiv \exists x \in S: P(x).\] \[\bigvee_{x \in S} P(x) \equiv P(x_1) \vee P(x_2) \vee \ldots \equiv \exists x \in S: P(x).\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_cf524b0eb075cd6d661f198cb1c393af94568acc_p1.png)
- Big Intersection:
![\[\bigcap_{i=1}^{n} A_i = A_1 \cap A_2 \cap \ldots \cap A_n.\] \[\bigcap_{i=1}^{n} A_i = A_1 \cap A_2 \cap \ldots \cap A_n.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_fdc7e227760302127f8ff48e2903b948500d5088_p1.png)
- Big Union:
![\[\bigcup_{i=1}^{n} A_i = A_1 \cup A_2 \cup \ldots \cup A_n.\] \[\bigcup_{i=1}^{n} A_i = A_1 \cup A_2 \cup \ldots \cup A_n.\]](/pinewiki/SummationNotation?action=AttachFile&do=get&target=latex_82e2381b46e0d4b2569faa80498d874949e01c4e_p1.png)
These all behave pretty much the way one would expect. One issue that is not obvious from the definition is what happens with an empty index set. Here the rule as with sums and products is to return the identity element for the operation. This will be True for AND, False for OR, and the empty set for union; for intersection, there is no identity element in general, so the intersection over an empty collection of sets is undefined.
40. RelationsAndFunctions
41. StructuralInduction
42. SolvingRecurrences
Notes on solving recurrences. These are originally from CS365, and emphasize asymptotic solutions; for CS202 we recommend also looking at GeneratingFunctions.
43. The problem
A recurrence or recurrence relation defines an infinite sequence by describing how to calculate the n-th element of the sequence given the values of smaller elements, as in:
- T(n) = T(n/2) + n, T(0) = T(1) = 1.
In principle such a relation allows us to calculate T(n) for any n by applying the first equation until we reach the base case. To solve a recurrence, we will find a formula that calculates T(n) directly from n, without this recursive computation.
Not all recurrences are solvable exactly, but in most of the cases that arises in analyzing recursive algorithms, we can usually get at least an asymptotic (i.e. big-Theta) solution (see AsymptoticNotation).
By convention we only define T by a recurrence like this for integer arguments, so the T(n/2) by convention represents either T(floor(n/2)) or T(ceiling(n/2)). If we want an exact solution for values of n that are not powers of 2, then we have to be precise about this, but if we only care about a big-Theta solution we will usually get the same answer no matter how we do the rounding.2 From this point on we will assume that we only consider values of n for which the recurrence relation does not produce any non-integer intermediate values.
44. Guess but verify
As when solving any other mathematical problem, we are not required to explain where our solution came from as long as we can prove that it is correct. So the most general method for solving recurrences can be called "guess but verify". Naturally, unless you are very good friends with the existential quantifier you may find it had to come up with good guesses. But sometimes it is possible to make a good guess by iterating the recurrence a few times and seeing what happens.
44.1. Forward substitution
Let's consider the recurrence
- T(n) = T(n-1) + 2n - 1
- T(0) = 0
The method of forward substitution proceeds by generating the first half-dozen or so terms in the sequence described by the recurrence, in the hope that it will turn out to be a sequence we recognize. In this case, we can calculate
n
T(n)
0
0
1
1
2
4
3
9
4
16
5
25
and at this point we can shout "Aha! This example was carefully rigged to give T(n)=n²!". Unfortunately, there are infinitely many sequences that start with these six numbers, so we can't be fully sure that this is the right answer until we prove it. So let's do so.
We will show that T(n) = n² satisfies the above recurrence for all n, by induction on n. The base case is n = 0; here T(0) = 0 = 0². For n > 0, we have
- T(n) = T(n-1) + 2n - 1 = (n-1)² + 2n - 1 = n² - 2n + 1 + 2n - 1 = n²,
and we are done.
(Here we used the induction hypothesis where we replace T(n-1) by (n-1)². We will usually not be very explicit about this.)
Here's a less rigged example:
- T(n) = T(floor(n/2)) + n, T(0) = 0.
Computing small cases gives
n
T(n)
0
0
1
1
2
3
3
4
4
7
5
8
6
10
7
11
8
15
which doesn't really tell us much about the behavior for large values. We can easily add a few powers of 2 to get an idea of what happens later:
16
31
32
63
64
127
From this we might guess that the solution satisfies T(n) <= 2n (or perhaps T(n) <= 2n - 1 for n > 0). So let's see if we can prove it:
- Base case
T(0) = 0 <= 2n.
- Induction step
For n > 0, T(n) = T(floor(n/2) + n <= 2 floor(n/2) + n <= 2(n/2) + n = 2n.
We might be able to prove a slightly tighter bound with more work, but this is enough to sho T(n) = O(n). Showing that T(n) = Omega(n) is trivial (since T(n) >= n), so we get T(n) = Θ(n) and we are done.
Applying the method of forward substitution requires a talent for recognizing sequences from their first few elements. If you are not born with this talent, you can borrow it from the mathematician Neal J. A. Sloane, or at least from his on-line Encyclopedia of Integer Sequences.
44.2. Backward substitution
Backward substitution, like forward substitution, tries to find a pattern from which we can guess a solution that we then prove using other techniques---but now we start with T(n) and expand it recursively using the recurrence.
For example, if we consider the same T(n) = T(n/2) + n recurrence from above, and assume for simplicity that n is a power of 2, then we get
- T(n) = n + T(n/2) = n + n/2 + T(n/4) = n + n/2 + n/4 + T(n/8) = n + n/2 + n/4 + n/8 + T(n/16) = ...
From this we might reasonably guess that T(n) is bounded by
![\[
\sum_{i=0}^{\infty} n/2^i
= n \sum_{i=0}^{\infty} 2^{-i}
= 2n.
\] \[
\sum_{i=0}^{\infty} n/2^i
= n \sum_{i=0}^{\infty} 2^{-i}
= 2n.
\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_ce432a442fea705571db622af3160a1a95ac7e3d_p1.png)
(See ComputingSums for how to compute this sum.) This is the same guess that we got from the method of forward substitution, so we prove that it works in the same way.
Note that in both methods we can omit how we got the guess from the final proof, though some readers might consider a refusal to explain a particularly good guess a form of teasing.
45. Converting to a sum
Some common recurrences appear often enough in AlgorithmAnalysis that it makes sense solve them once in general form, and then just apply the general solution as needed. You can either memorize these solutions, or, better yet, remember enough of how they are derived to be able to reconstruct them.
45.1. When T(n) = T(n-1) + f(n)
This is the easiest case, which usually appears in DecreaseAndConquer algorithms. Here it is easy to see (and can be proved by induction) that
![\[T(n) = \sum_{i=1}^{n} f(i) + T(0).\] \[T(n) = \sum_{i=1}^{n} f(i) + T(0).\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_a51cca183430309df05055f568fd7ee1f1ddcb13_p1.png)
Example: for T(n) = T(n-1) + n², we immediately have
![\[T(n) = \sum_{i=1}^{n} i^2 + T(0),\] \[T(n) = \sum_{i=1}^{n} i^2 + T(0),\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_57c22bcc9ebe2252c52ea38ec6c2ece5a3cc01a5_p1.png)
which we can quickly show is Θ(n³) in any number of ways (see ComputingSums).
45.2. When T(n) = aT(n-1) + f(n)
This is a little trickier, because as the arguments to the f's drop, they are multiplied by more and more a's. After some backward substitution it is not hard to recognize the pattern
![\[T(n) = \sum_{i=0}^{n-1} a^i f(n-i) + a^nT(0).\] \[T(n) = \sum_{i=0}^{n-1} a^i f(n-i) + a^nT(0).\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_8251e2f0accae72107993c189e2b8ec463de6208_p1.png)
Example: T(n) = 2T(n-1) + n. Then from the formula
![\[T(n) = \sum_{i=0}^{n-1} 2^i (n-i) + 2^n T(0).\] \[T(n) = \sum_{i=0}^{n-1} 2^i (n-i) + 2^n T(0).\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_823840b3338898e50b81bcbf5dc891b27d77537d_p1.png)
This turns out to be a rather painful sum to solve exactly, but we can reasonably guess that it's somewhere between 2n and 2nn, and try guess-but-verify to whittle the range down further.
45.3. When T(n) = aT(n/b) + f(n)
This form of recurrence tends to arise from DivideAndConquer algorithms. For n = bk, n/b = bk-1, which makes this recurrence a thinly-disguised version of the last one. We thus have
![\[T(n)
= \sum_{i=0}^{\log_b n-1} a^i f(n/b^i) + a^{\log_b n} T(1)
= \sum_{i=0}^{\log_b n-1} a^i f(n/b^i) + n^{\log_b a} T(1),
\] \[T(n)
= \sum_{i=0}^{\log_b n-1} a^i f(n/b^i) + a^{\log_b n} T(1)
= \sum_{i=0}^{\log_b n-1} a^i f(n/b^i) + n^{\log_b a} T(1),
\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_b4216c573788f40b04e5d07e0de980f0225a6a18_p1.png)
where logb x = log x / log b, the base-b logarithm of x.
These sums can get ugly fast. Here's an unusually clean case:
- T(n) = 2T(n/2) + n.
Then
![\[T(n)
= \sum_{i=0}^{\lg n - 1} 2^i (n/2^i) + 2^{\lg n} T(1)
= \sum_{i=0}^{\lg n - 1} n + nT(1)
= n \lg n + n T(1)),
\] \[T(n)
= \sum_{i=0}^{\lg n - 1} 2^i (n/2^i) + 2^{\lg n} T(1)
= \sum_{i=0}^{\lg n - 1} n + nT(1)
= n \lg n + n T(1)),
\]](/pinewiki/SolvingRecurrences?action=AttachFile&do=get&target=latex_b672c34f746640afd0a1cbc76d973e4bcfbe712c_p1.png)
provided, of course, that n is a power of 2. For values of n that are not powers of 2, or for less conveniently constructed recurrences of this form, it is often better to skip directly to the Master Theorem.
46. The Master Theorem
The Master Theorem provides instant asymptotic solutions for many recurrences of the form T(n) = aT(n/b) + f(n), that apply for all values of n (not just powers of b). It is based on applying the analysis of the preceding section to various broad families of functions f, and then extending the results using a monotonicity argument to values of n that are not powers of b. Here we sketch out the proof; see LevitinBook Appendix B for a more detailed argument.
If f(n) = 0, then the recurrence is simply T(n) = aT(n/b). This has solution T(n) = nlog[b] a T(1) = Θ(nlog[b] a). (Example: T(n) = 4T(n/2) has solution Θ(nlg 4) = Θ(n²).) We classify different cases of the Master Theorem based on how f(n) compares to this default solution.
Recall that the general solution is
T(n) = Sigma,,i=0 to log[b] n - 1 ai f(n/bi) + nlog[b] a T(1).
We assume that T(1) = Θ(1) throughout.
Suppose that f(x) = xc. Then ai f(n/bi) = ai nc / bic = nc (a/bc)i. The sum is then a geometric series with ratio (a/bc), and its behavior depends critically on whether (a/bc) is less than 1, equal to 1, or greater than 1.
If (a/bc) is less than 1, then Sigmai=0 to infinity nc (a/bc)i = nc/(1-(a/bc)) = O(nc). This case arises when log(a/bc) = log a - c log b is less than zero, which occurs precisely when c > log a / log b = logb a. So if f(n) = nc, the f(n) term in the sum dominates both the rest of the sum and the nlog[b] a term, and we get T(n) = Θ(f(n)). If f(n) is Omega(nc), but satisfies the additional technical requirement that af(n/b) <= (1-delta) f(n) for all n and some fixed delta > 0, then the geometric series argument still works with factor (1-delta), and we still get T(n) = Θ(f(n)). This covers the case where f(n) = Omega(nlog[b] a + epsilon).
If (a/bc) is equal to 1, then every term in the sum is the same, and the total is f(n) logb n. In this case c = logb a, so f(n) = nlog[b] a and f(n) logb n dominates (barely) the T(1) term. An extended version of this analysis shows that the solution is T(n) = Θ(f(n) log n) when f(n) = Θ(nlog[b] a).
Finally, if (a/bc) is greater than 1, we have a geometric series whose sum is proportional to its last term, which can be shown to be asymptotically smaller than the T(1) term. This case gives T(n) = Θ(nlog[b] a) for any f(n) = O(nlog[b] a - epsilon).
Summarizing, we have
If f(n) = O(nlog[b] a - epsilon), then T(n) = Θ(nlog[b] a).
If f(n) = Θ(nlog[b] a), then T(n) = Θ(f(n) log n).
If f(n) = Omega(nlog[b] a + epsilon), and there exists c < 1 such that a f(n/b) <= c f(n), then T(n) = Θ(f(n)).
These three cases do not cover all possibilities (consider T(n) = 2T(n/2) + n log n), but they will handle most recurrences of this form you are likely to encounter.
47. PigeonholePrinciple
48. HowToCount
Contents
49. What counting is
Recall that in SetTheory we formally defined each natural number as the set of all smaller natural numbers, so that n = { 0, 1, 2, ..., n-1 }. Call a set finite if it can be put in one-to-one correspondence with some natural number n. For example, the set S = { Larry, Moe, Curly } is finite because we can map Larry to 0, Moe to 1, and Curly to 2, and get a bijection between S and the set 3 = { 0, 1, 2 }. The size or cardinality of a finite set S, written |S| or #S, is just the natural number it can be put in one-to-one correspondence with; that this is well-defined (gives a unique size for each finite set) follows from the Pigeonhole Principle (see below). In general, a cardinal number is a representative of some class of sets that can all put connected to each other by bijections; these include infinite cardinal numbers, discussed below.
Usually we will not provide an explicit bijection to compute the size of a set, but instead will rely on standard counting principles (see below). A proof that a set has a certain size (or that two sets have the same size) that does provide an explicit bijection is called a combinatorial proof. For sets of complicated objects, such proofs often provide additional insight into the structure of the objects.
49.1. Countable and uncountable sets
A set S is infinite if there is a bijection between S and some proper subset of S (proper subset means a subset that isn't equal to S), or equivalently if it can't be put in one-to-one correspondence with any natural number. One of the smallest infinite sets is just the set of all naturals ℕ. Any infinite set also has a cardinality; as for finite sets, the cardinality of an infinite set is defined based on what other sets it can be put into one-to-one correspondence with, and different infinite sets may have different cardinalities.
The smallest cardinality is ℵ0 (pronounced aleph-nought), the cardinality of ℕ. Any set S for which there exists a bijection f:S↔ℕ has cardinality ℵ0. Examples include the set of all pairs of natural numbers (which can be mapped to single natural numbers using various encodings), the set of integers ℤ, the set of rationals ℚ, the set of all finite sequences of natural numbers (using more sophisticated encodings), the set of all computer programs (represent them as sequences of natural numbers, e.g., using ASCII encoding), the set of all possible finite-length texts in any language with a countable output, or the set of all mathematical objects that can be explicitly defined (each such definition is a finite text).
Sets with cardinality ℵ0 or less are called countable; sets with cardinality exactly ℵ0 are countably infinite.
That there are larger cardinalities is a consequence of a famous proof due to Georg Cantor, the diagonalization argument:
- Theorem
- Let S be any set. Then there is no surjection f:S→℘S.
- Proof
- Let f:S→℘S. We will show that f is not surjective, by constructing a subset A of S such that A≠f(x) for any x in S. Let A = { x | x∉f(x) }. Now choose some x and consider f(x). We have x∈A if and only if x∉f(x); so x is in exactly one of A and f(x), and in particular A≠f(x). It follows that A≠f(x) for all x, and thus that A isn't in the range of f.
Since any bijection is also a surjection, this means that |S| ≠ |℘S|. For finite sets, this is pretty easy to show directly: it just says that n<2n for all natural numbers n. For infinite sets, it means, for example, that |ℕ| ≠ |℘ℕ|, or equivalently that |℘ℕ| > ℵ0. This means that ℘ℕ is uncountable.
The next largest cardinal after ℵ0 is called ℵ1 (aleph-one). The standard axioms of SetTheory provably can't tell us whether |℘ℕ| = ℵ1 or not, but if we assume the Continuum hypothesis we can assert that |℘ℕ| = ℵ1. In this case ℵ1 not only gives the cardinality of the power set of the naturals, but also the cardinality of the set of real numbers ℝ, the set of complex numbers ℂ, the set of finite sequences of reals, etc. It does not give the cardinality of ℘ℝ or the set of functions f:ℝ→ℝ; these live (assuming a strengthened version of the Continuum hypothesis) up at ℵ2.
Because Cantor's theorem applies even to these bigger sets, there is an infinite sequence of increasingly large cardinalities ℵ0, ℵ1, ℵ2, ℵ3, ... . Pretty much anything past about ℵ1 falls into the category of incomprehensibly large (not an actual mathematical term).
50. Basic counting techniques
Our goal here is to compute the size of some set of objects, e.g. the number of subsets of a set of size n, the number of ways to put k cats into n boxes so that no box gets more than one cat, etc.
In rare cases we can use the definition of the size of a set directly, by constructing a bijection between the set we care about and some natural number. For example, the set Sn = { x ∈ ℕ | x < n2 /\ ∃y: x = y2 } has exactly n members, because we can generate it by applying the one-to-one correspondence f(y) = y2 to the set { 0, 1, 2, 3, ..., n-1 } = n. But most of the time constructing an explicit one-to-one correspondence is too time-consuming or too hard, so having a few lemmas around that tell us what the size of a set will be can be handy.
50.1. Reducing to a previously-solved case
If we can produce a bijection between a set A whose size we don't know and a set B whose size we do, then we get |A|=|B|. Pretty much all of our proofs of cardinality will end up looking like this.
50.2. Showing |A| ≤ |B| and |B| ≤ |A|
We write |A| ≤ |B| if there is an injection f:A→B, and similarly |B| ≤ |A| if there is an injection g:B→A. If both conditions hold, then there is a bijection between A and B, showing |A| = |B|. This fact is trivial for finite sets (it is a consequence of the Pigeonhole Principle), but for infinite sets—even though it is still true—the actual construction of the bijection is a little trickier. See Cantor-Bernstein-Schroeder theorem if you really want the gory details.
Similarly, if we write |A| ≥ |B| to indicate that there is a surjection from A to B, then |A| ≥ |B| and |B| ≥ |A| implies |A| = |B|. The easiest way to show this is to observe that if there is a surjection f:A→B, then we can get an injection f':B→A by letting f'(y) be any element of { x | f(x) = y } (this requires the Axiom of Choice, but pretty much everybody assumes the Axiom of Choice).
Examples:
|ℚ| = |ℕ|. Proof: |ℕ| ≤ |ℚ| because we can map any n in ℕ to the same value in ℚ; this is clearly an injection. To show |ℚ| ≤ |ℕ|, observe that we can encode any element ±p/q of ℚ, where p and q are both natural numbers, as a triple <sign, p, q> where sign ∈ {0,1} indicates + (0) or - (1); this encoding is clearly injective. Then use the bijection from ℕ×ℕ to ℕ twice to crunch this triple down to a single natural number, getting an injection from ℚ to ℕ.
50.3. Sum rule
The sum rule says
- If A∩B=Ø, then |A∪B| = |A| + |B|.
Proof: Let f:A→|A| and g:B→|B| be bijections. Define h:A∪B→(|A|+|B|) by the rule h(x) = f(x) for x∈A, h(x) = |A|+g(x) for x∈B. We need to show that h is a bijection; we will do so by first showing that it is injective, then that it is surjective. Let x and y be distinct elements of A∪B. If x and y are both in A, then h(x) = f(x) ≠ f(y) = h(y); similarly if x and y are both in B, h(x) = |A|+g(x) ≠ |A| + g(y) = h(y). If x is in A and y in B, then h(x) = f(x) < |A|, and h(y) = g(y) + |A| ≥ |A|; it follows that h(x) ≠ h(y). The remaining case is symmetric. To show h is surjective, let m∈(|A|+|B|). If m < |A|, there exists some x∈A such that h(x) = f(x) = m. Otherwise, we have |A| ≤ m < |A|+|B|, so 0 ≤ m - |A| < |B|, and there exists some y∈B such that g(y) = m-|A|. But then h(y) = g(y)+|A| = m-|A|+|A| = m.
Generalizations: If A1, A2, A3 ... Ak are pairwise disjoint (i.e. Ai ∩ Aj = Ø for all i ≠j), then
![\[\left|\bigcup_{i=1}^{k} A_i\right| = \sum_{i=1}^{k} |A_i|.\] \[\left|\bigcup_{i=1}^{k} A_i\right| = \sum_{i=1}^{k} |A_i|.\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_5a5f48b7f0f6330b5434fcefcfaa8308e3c5b8bd_p1.png)
The proof is by induction on k.
50.3.1. Examples
- As I was going to Saint Ives, I met a man with 7 wives, 28 children, 56 grandchildren, and 122 great-grandchildren. Assuming these sets do not overlap, how many people did I meet? Answer: 1+7+28+56+122=214.
50.3.2. For infinite sets
The sum rule works for infinite sets, too; technically, the sum rule is used to define |A|+|B| as |A∪B| when A and B are disjoint. This makes cardinal arithmetic a bit wonky: if at least one of A and B is infinite, then |A| + |B| = max(|A|,|B|), since we can space out the elements of the larger of A and B and shoehorn the other into the gaps.
50.3.3. The Pigeonhole Principle
A consequence of the sum rule is that if A and B are both finite and |A| > |B|, you can't have an injection from A to B. The proof is by contraposition. Suppose f:A→B is an injection. Write A as the union of f-1(x) for each x∈B, where f-1(x) is the set of y in A that map to x. Because each f-1(x) is disjoint, the sum rule applies; but because f is an injection there is at most one element in each f-1(x). It follows that  . (Question: Why doesn't this work for infinite sets?)
. (Question: Why doesn't this work for infinite sets?)
The Pigeonhole Principle generalizes in an obvious way to functions with larger domains; if f:A→B, then there is some x in B such that |f-1(x)| ≥ |A|/|B|.
50.4. Inclusion-exclusion (with two sets)
What if A and B are not disjoint, i.e., if A∩B is not Ø? In this case adding |A| to |B| will count any element that appears in both sets twice. We can get the size of |A∪B| by subtracting off the overcount, obtaining this formula, which works for all A and B:
- |A∪B| = |A| + |B| - |A∩B|
To prove that the formula works, we use the sum rule. Observe that A = (A∩B) ∪ (B-A) and that the union in this case is disjoint (recall that A-B is the set of all elements that are in A but not in B). A similar decomposition works for B, so we have
- |A| + |B| = |A∩B| + |B-A| + |B∩A| + |A-B| = |A∪B| + |A∩B|.
Here we are again using the sum rule: A∪B is the disjoint union of A-B, B-A, and A∩B. Subtracting the |A∩B| term from both sides gives the formula we originally wanted.
This is a special case of the inclusion-exclusion formula, which can be used to compute the size of the union of many sets using the size of pairwise, triple-wise, etc. intersections of the sets.
50.4.1. For infinite sets
Subtraction doesn't work very well for infinite quantities (while ℵ0+ℵ0=ℵ0, that doesn't mean ℵ0=0). So the closest we can get to the inclusion-exclusion formula is that |A| + |B| = |A∪B| + |A∩B|. If at least one of A or B is infinite, then |A∪B| is also infinite, and since |A∩B| ≤ |A∪B| we have |A∪B| + |A∩B| = |A∪B| by the usual but bizarre rules of cardinal arithmetic. So for infinite sets we have the rather odd result that |A∪B| = |A| + |B| = max(|A|,|B|) whether the sets overlap or not.
50.4.2. Combinatorial proof
We can prove |A| + |B| = |A∪B| + |A∩B| combinatorially, by turning both sides of the equation into disjoint unions (so the sum rule works) and then providing an explicit bijection between the resulting sets. The trick is that we can always force a union to be disjoint by tagging the elements with extra information; so on the left-hand side we construct L = {1}×A ∪ {2}×B, and on the right-hand side we construct R = {1}×(A∪B) ∪ {2}×(A∩B). It is easy to see that both unions are disjoint, because we are always taking the union of a set of ordered pairs that start with 1 with a set of ordered pairs that start with 2, and no ordered pair can start with both tags; it follows that |L| = |A| + |B| and |R| = |A∪B| + |A∩B|. Now define the function f:L→R by the rule
- f((1,x)) = (1,x).
- f((2,x)) = (2,x) if x∈B∩A
- f((2,x)) = (1,x) if x∈B\A.
Observe that f is surjective, because for any (1,x) in {1}×(A∪B), either x is in A and (1,x) = f((1,x)) where (1,x) ∈ L, or x is in B\A and (1,x) = f((2,x)) where (2,x) ∈ L. It is also true that f is injective; the only way for it not to be is if f((1,x)) = f((2,x)) = (1,x) for some x. Suppose this occurs. Then x ∈ A (because of the 1 tag) and x ∈ B\A (because (2,x) is only mapped to (1,x) if x∈B\A). But x can't be in both A and B\A, so we get a contradiction.
50.5. Product rule
The product rule says that for any sets A and B
- |A×B| = |A|·|B|.
Recall that A×B is the Cartesian product of A and B, the set of all ordered pairs whose first element comes from A and whose second comes from B.
Proof (for finite sets): Let f:A→|A| and g:B→|B| be bijections. Construct a new function h:|A×B|→(|A|·|B|) by the rule h(<a,b>) = a·|B| + b. Showing that h is a bijection is left as an exercise to the reader (hint: use the DivisionAlgorithm).
The general form is
![\[\left|\prod_{i=1}^{k} A_i\right| = \prod_{i=1}^{k} |A_i|,\] \[\left|\prod_{i=1}^{k} A_i\right| = \prod_{i=1}^{k} |A_i|,\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_040b5bf066d1fb1c05499fdc5d3f8f8bbdfa91f1_p1.png)
where the product on the left is a Cartesian product and the product on the right is an ordinary integer product.
50.5.1. Examples
As I was going to Saint Ives, I met a man with seven sacks, and every sack had seven cats. How many cats total? Answer: Label the sacks 0,1,2,...,6, and label the cats in each sack 0,1,2,...,6. Then each cat can be specified uniquely by giving a pair <sack number, cat number>, giving a bijection between the set of cats and the set 7×7. Since the |7×7|=7·7=49, we have 49 cats.
Dr Frankenstein's trusty assistant Igor has brought him 6 torsos, 4 brains, 8 pairs of matching arms, and 4 pairs of legs. How many different monsters can Dr Frankenstein build? Answer: there is a one-to-one correspondence between possible monsters and 4-tuples of the form <torso, brain, pair of arms, pair of legs>; the set of such 4-tuples has 6·4·8·4=728 members.
How many different ways can you order n items? Call this quantity n! (i.e., n factorial). With 0 or 1 items, there is only one way; so we have 0!=1!=1. For n > 1, there are n choices for the first item, leaving n-1 items to be ordered. From the product rule we thus have n! = n·(n-1)!, which we could also expand out as

As a generalization of the previous example, we can count the number of ways P(n,k) we can pick an ordered subset of k of n items without replacement, also known as picking a k-permutation. There are n ways to pick the first item, n-1 to pick the second, and so forth, giving a total of
![\[P(n,k) = \prod_{i=n-k+1}^{n} i = \frac{n!}{(n-k)!}\] \[P(n,k) = \prod_{i=n-k+1}^{n} i = \frac{n!}{(n-k)!}\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_9546ac53334e0393316bc0c3890b4d7a44365b08_p1.png)
such k-permutations by the product rule.
Among combinatorialists, the notation (n)k (pronounced "n lower-factorial k") is more common than P(n,k) for n·(n-1)·(n-2)·...·(n-k+1). As an extreme case we have (n)n = n·(n-1)·(n-2)·...·(n-n+1) = n·(n-1)·(n-2)·...·1 = n!.
50.5.2. For infinite sets
The product rule also works for infinite sets, becasue we again use it as a definition: for any A and B, |A|⋅|B| is defined to be |A×B|. One oddity for infinite sets is that this definition gives |A|⋅|B| = |A|+|B| = max(|A|,|B|), because if at least one of A and B is infinite, it is possible to construct a bijection between A×B and the larger of A and B. (Infinite sets are strange.)
50.6. Exponent rule
Given sets A and B, let AB be the set of functions f:B→A. Then |AB| = |A||B|.
If |B| is finite, this is just a |B|-fold application of the product rule: we can write any function f:B→A as a sequence of length |B| that gives the value in A for each input in B. Since each element of the sequence contributes |A| possible choices, we get |A|^|B| choices total.
For infinite sets, the exponent rule is a definition of |A||B|. The behavior of exponentiation for infinite cardinals is very strange indeed; see here for some properties of cardinal exponentiation if you are really interested.
To give a flavor of how exponentiation works for arbitrary sets, here's a combinatorial proof of the usual arithmetic fact that xaxb = xa+b, for any cardinal numbers x, a, and b. Let x = |X| and let a = |A| and b = |B| where A and B are disjoint (we can always use the tagging trick that we used for inclusion-exclusion to make A and B be disjoint). Then xaxb = |XA×XB| and xa+b = |XA∪B|. We will now construct an explicit bijection f:XA∪B→XA×XB. The input to f is a function g:A∪B→X; the output is a pair of functions (gA:A→X,gB:B→X). We define gA by gA(x) = g(x) for all x in A (this makes gA the restriction of g to A, usually written as g|A or g⇂A); similarly gB = g|B. This is easily seen to be a bijection; if g = h, then f(g) = (g|A,g|B) = f(h) = (h|A,h|B), and if g≠h there is some x for which g(x)≠h(x), implying g|A≠h|A (if x is in A) or g|B≠h|B (if x is in B).
50.7. Counting the same thing in two different ways
An old farm joke:
- Q: How do you count a herd of cattle? A: Count the legs and divide by four.
Sometimes we can compute the size of a set S by using it (as an unknown variable) to compute the size of another set T (as a function of |S|), and then using some other way to count T to find its size, finally solving for |S|. This is known as counting two ways and is surprisingly useful when it works. We will assume that all the sets we are dealing with are finite, so we can expect things like subtraction and division to work properly.
Example: Let S be an n-element set, and consider the set Sk = { A⊆S | |A| = k }. What is |Sk|? Answer: First we'll count the number m of sequences of k elements of S with no repetitions. We can get such a sequence in two ways:
By picking a size-k subset A and then choosing one of k! ways to order the elements. This gives m = |Sk|·k!.
By choosing the first element in one of n ways, the second in one of n-1, the third in one of n-2 ways, and so on until the k-th element, which can be chosen in one of n-k+1 ways. This gives m = (n)k = n·(n-1)·(n-2)·...(n-k+1), which can be written as n!/(n-k)!. (Here we are using the factors in (n-k)! to cancel out the factors in n! that we don't want.)
So we have m = |Sk|·k! = n!/(n-k)!, from which we get
![\[|S_k| = \frac{n!}{k!\cdot(n-k)!}.\] \[|S_k| = \frac{n!}{k!\cdot(n-k)!}.\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_9b8a94cfb623403e675f772a0881a63751fc8e49_p1.png)
This quantity turns out to be so useful that it has a special notation:
![\[{n \choose k} \stackrel{\mbox{\scriptsize def}}{=} \frac{n!}{k!\cdot(n-k)!}.\] \[{n \choose k} \stackrel{\mbox{\scriptsize def}}{=} \frac{n!}{k!\cdot(n-k)!}.\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_e366281ab4ebd8fbcd70ff314ed25435c3817cfb_p1.png)
where the left-hand side is known as a binomial coefficient and is pronounced "n choose k." We discuss BinomialCoefficients at length on their own page. The secret of why it's called a binomial coefficient will be revealed when we talk about GeneratingFunctions.
Example: Here's a generalization of binomial coefficients: let the multinomial coefficient
![\[{n \choose n_1 \; n_2 \; \ldots \; n_k}\] \[{n \choose n_1 \; n_2 \; \ldots \; n_k}\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_82fe253b33c2771ecb4281f4618dffb9f715bf25_p1.png)
be the number of different ways to distribute n items among k bins where the i-th bin gets exactly ni of the items and we don't care what order the items appear in each bin. (Obviously this only makes sense if n1+n2+...+nk=n.) Can we find a simple formula for the multinomial coefficient?
Here are two ways to count the number of permutations of the n-element set:
- Pick the first element, then the second, etc. to get n! permuations.
- Generate a permutation in three steps:
Pick a partition of the n elements into groups of size n1, n2, ... nk.
- Order the elements of each group.
- Paste the groups together into a single ordered list.
There are
![\[{n \choose n_1 \; n_2 \; \ldots \; n_k}\] \[{n \choose n_1 \; n_2 \; \ldots \; n_k}\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_82fe253b33c2771ecb4281f4618dffb9f715bf25_p1.png)
ways to pick the partition and
![\[n_1! \cdot n_2! \cdots n_k!\] \[n_1! \cdot n_2! \cdots n_k!\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_0859d6490d847b04f00418639e3723d318dfbb11_p1.png)
ways to order the elements of all the groups, so we have
![\[n! = {n \choose n_1 \; n_2 \; \ldots \; n_k} \cdot n_1! \cdot n_2! \cdots n_k!\] \[n! = {n \choose n_1 \; n_2 \; \ldots \; n_k} \cdot n_1! \cdot n_2! \cdots n_k!\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_c049908f4b6b9553807c1324b102e2f22b3daa9a_p1.png)
which we can solve to get
![\[{n \choose n_1 \; n_2 \; \ldots \; n_k} = \frac{n!}{n_1! \cdot n_2! \cdots n_k!}\] \[{n \choose n_1 \; n_2 \; \ldots \; n_k} = \frac{n!}{n_1! \cdot n_2! \cdots n_k!}\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_d2b8ea8ef2a88de74811be84c92d1c0578f67669_p1.png)
This also gives another way to derive the formula for a binomial coefficient, since
![\[{n \choose k} = {n \choose k \;\; (n-k)} = \frac{n!}{k!\cdot (n-k)!}\] \[{n \choose k} = {n \choose k \;\; (n-k)} = \frac{n!}{k!\cdot (n-k)!}\]](/pinewiki/HowToCount?action=AttachFile&do=get&target=latex_0efee6ebd21ce995f8c0ec56a2e08cc1515ef41e_p1.png)
51. Applying the rules
If you're given some strange set to count, look at the structure of its description:
If it's given by a rule of the form x is in S if either P(x) or Q(x) is true, use the sum rule (if P and Q are mutually exclusive) or inclusion-exclusion. This includes sets given by recursive definitions, e.g. x is a tree of depth at most k if it is either (a) a single leaf node (provided k > 0) or (b) a root node with two subtrees of depth at most k-1. The two classes are disjoint so we have T(k) = 1 + T(k-1)2 with T(0) = 0.3
For objects made out of many small components or resulting from many small decisions, try to reduce the description of the object to something previously known, e.g. (a) a word of length k of letters from an alphabet of size n allowing repetition (there are nk of them, by the product rule); (b) a word of length k not allowing repetition (there are (n)k of them—or n! if n = k); (c) a subset of k distinct things from a set of size n, where we don't care about the order (there are
 of them); any subset of a set of n things (there are 2n of them—this is a special case of (a), where the alphabet encodes non-membership as 0 and membership as 1, and the position in the word specifies the element). Some examples:
of them); any subset of a set of n things (there are 2n of them—this is a special case of (a), where the alphabet encodes non-membership as 0 and membership as 1, and the position in the word specifies the element). Some examples: The number of games of Tic-Tac-Toe assuming both players keep playing until the board is filled is obtained by observing that each such game can be specified by listing which of the 9 squares are filled in order, giving 9! = 362,880 distinct games. Note that we don't have to worry about which of the 9 moves are made by X and which by O, since the rules of the game enforce it. (If we only consider games that end when one player wins, this doesn't work: probably the easiest way to count such games is to send a computer off to generate all of them. This horrible program says there are 255168 possible games and 958 distinct final positions.)
The number of completely-filled-in Tic-Tac-Toe boards can be obtained by observing that any such board has 5 X's and 4 O's. So there are
 = 126 such positions. (Question: Why would this be smaller than the actual number of final positions?)
= 126 such positions. (Question: Why would this be smaller than the actual number of final positions?)
Sometimes reducing to a previous case requires creativity. For example, suppose you win n identical cars on a game show and want to divide them among your k greedy relatives. Assuming that you don't care about fairness, how many ways are there to do this?
If it's ok if some people don't get a car at all, then you can imagine putting n cars and k-1 dividers in a line, where relative 1 gets all the cars up to the first divider, relative 2 gets all the cars between the first and second dividers, and so forth up to relative k who gets all the cars after the (k-1)th divider. Assume that each car—and each divider—takes one parking space. Then you have n+k-1 parking spaces with k-1 dividers in them (and cars in the rest). There are exactly
 ways to do this.
ways to do this. Alternatively, suppose each relative demands at least 1 car. Then you can just hand out one car to each relative to start with, leaving n-k cars to divide as in the previous case. There are
 ways to do this.
ways to do this.
Finding such correspondences is a central part of enumerative combinatorics, the branch of mathematics that deals with counting things.
52. An elaborate counting problem
Suppose you have the numbers { 1, 2, .., 2n }, and you want to count how many sequences of k of these numbers you can have that are (a) increasing (a[i] < a[i+1] for all i), (b) decreasing (a[i] ≥ a[i+1] for all i), or (c) made up only of even numbers.
This is the union of three sets A, B, and C, corresponding to the three cases. The first step is to count each set individually; then we can start thinking about applying inclusion-exclusion to get the size of the union.
For A, any increasing sequence can be specified by choosing its elements (the order is determined by the assumption it is increasing). So we have  .
.
For B, by symmetry we have  .
.
For C, we are just looking at nk possible sequences, since there are n even numbers we can put in each position.
Inclusion-exclusion says that |A∪B∪C| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| + |A∪B∪C|. It's not hard to see that A∩B = ∅ when k is at least 24, so we can reduce this to |A| + |B| + |C| - |A∩C| - |B∩C|. To count A∩C, observe that we are now looking at increasing sequences chosen from the n possible even numbers; so there are exactly  of them, and similarly for B∩C. Summing up gives a total of
of them, and similarly for B∩C. Summing up gives a total of

sequences satisfying at least one of the criteria.
Note that we had to assume k = 2 to get A∩B=∅, so this formula might require some adjustment for k<2. In fact we can observe immediately that the unique empty sequence for k=1 fits in all of A, B, and C, so in this case we get 1 winning sequence (which happens to be equal to the value in the formula, because here A∩B=∅ for other reasons), and for k=1 we get 2n winning sequences (which is less than the value 3n given by the formula).
To test that the formula works for at least some larger values, let n=3 and k=2. Then the formula predicts  total sequences.5 And here they are (generated by seqs.py run as python seqs.py 6 2):
total sequences.5 And here they are (generated by seqs.py run as python seqs.py 6 2):
[1, 2] [1, 3] [1, 4] [1, 5] [1, 6] [2, 1] [2, 2] [2, 3] [2, 4] [2, 5] [2, 6] [3, 1] [3, 2] [3, 4] [3, 5] [3, 6] [4, 1] [4, 2] [4, 3] [4, 4] [4, 5] [4, 6] [5, 1] [5, 2] [5, 3] [5, 4] [5, 6] [6, 1] [6, 2] [6, 3] [6, 4] [6, 5] [6, 6]
53. Further reading
RosenBook does basic counting in chapter 5 and more advanced counting (including SolvingRecurrences and using GeneratingFunctions) in chapter 7. BiggsBook chapters 6 and 10 give a basic introduction to counting, with more esoteric topics in chapters 11 and 12. ConcreteMathematics has quite a bit on counting various things.
54. BinomialCoefficients
Contents
The binomial coefficient "n choose k", written
![\[{n \choose k} = \frac{(n)_{k}}{k!} = \frac{n!}{k!\cdot (n-k)!},\] \[{n \choose k} = \frac{(n)_{k}}{k!} = \frac{n!}{k!\cdot (n-k)!},\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_32cb3e00e1f9363061103682cdeb3e8f4c485d3a_p1.png)
counts the number of k-element subsets of an n-element set.
The name arises from the binomial theorem, which says that
![\[(x+y)^n = \sum_{k=0}^{\infty} {n \choose k} x^k y^{n-k}.\] \[(x+y)^n = \sum_{k=0}^{\infty} {n \choose k} x^k y^{n-k}.\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_15f74fcd776b1e3fac9c382877f20558200f5b85_p1.png)
For integer n, we can limit ourselves to letting k range from 0 to n. The most general version of the theorem lets k range over all of ℕ, and relies on the binomial coefficient to zero out the extra terms. It holds for any integer n ≥ 0 or (with a suitable definition of binomial coefficients) for any n if |x/y| < 1 (which guarantees that the sum converges).
The connection to counting subsets is straightforward: expanding (x+y)n using the distributive law gives 2n terms, each of which is a unique sequence of n x's and y's. If we think of the x's in each term as labeling a subset of the n positions in the term, the terms that get added together to get xkyn-k correspond one-to-one to subsets of size k. So there are

such terms, accounting for the coefficient on the right-hand side.
55. Recursive definition
If we don't like computing factorials, we can also compute binomial coefficients recursively.
Base cases:
- If k = 0, then there is exactly one zero-element set of our n-element set—it's the empty set—and we have

If k > n, then there are no k-element subsets, and we have

Recursive step: We'll use Pascal's identity, which says that
![\[{n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}.\] \[{n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}.\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_b7abf97f5a3722349048f6b2aedbd941e134a165_p1.png)
The proof of this identity is combinatorial, which means that we will construct an explicit bijection between a set counted by the left-hand side and a set counted by the right-hand side. This is often one of the best ways of understanding simple binomial coefficient identities.
On the left-hand side, we are counting all the k-element subsets of an n-element set S. On the right hand side, we are counting two different collections of sets: the (k-1)-element and k-element subsets of an (n-1)-element set. The trick is to recognize that we get an (n-1)-element set S' from our original set by removing one of the elements x. When we do this, we affect the subsets in one of two ways:
- If the subset doesn't contain x, it doesn't change. So there is a one-to-one correspondence (the identity function) between k-subsets of S that don't contain x and k-subsets of S'. This bijection accounts for the first term on the right-hand side.
- If the subset does contain x, then we get a (k-1)-element subset of S' when we remove it. Since we can go back the other way by reinserting x, we get a bijection between k-subsets of S that contain x and (k-1)-subsets of S'. This bijection accounts for the second term on the right-hand side.
Adding the two cases together (using the sum rule), we conclude that the identity holds.
Using the base case and Pascal's identity, we can construct Pascal's triangle, a table of values of binomial coefficients:
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 ...
Each row corresponds to increasing values of n, and each column to increasing values of k, with

in the upper left-hand corner. To compute each entry, we add together the entry directly above it and the entry diagonally to the left.
55.1. Pascal's identity: algebraic proof
Using the binomial theorem plus a little bit of algebra, we can prove Pascal's identity without using a combinatorial argument (this is not necessarily an improvement). The additional fact we need is that if we have two equal series
![\[\sum_{k=0}^{\infty} a_k x^k = \sum_{k=0}^{\infty} b_k x^k\] \[\sum_{k=0}^{\infty} a_k x^k = \sum_{k=0}^{\infty} b_k x^k\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_37c4743c8ff8372bfa2178726fef1ce776216bf1_p1.png)
then ai = bi for all i.
Here's the proof:
![\begin{eqnarray*}
\sum_{k=0}^n {n \choose k} x^k
&=& (1+x)^n \\
&=& (1+x)(1+x)^{n-1} \\
&=& (1+x)^{n-1} + x(1+x)^{n-1} \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + x \sum_{k = 0}^{n-1} {n-1 \choose k} x^k \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + \sum_{k = 0}^{n-1} {n-1 \choose k} x^{k+1} \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + \sum_{k = 1}^{n} {n-1 \choose k-1} x^{k} \\
&=& \sum_{k = 0}^{n} {n-1 \choose k} x^k + \sum_{k = 0}^{n} {n-1 \choose k-1} x^{k} \\
&=& \sum_{k = 0}^{n} \left[{n-1 \choose k} + {n-1 \choose k-1}\right] x^{k}.
\end{eqnarray*} \begin{eqnarray*}
\sum_{k=0}^n {n \choose k} x^k
&=& (1+x)^n \\
&=& (1+x)(1+x)^{n-1} \\
&=& (1+x)^{n-1} + x(1+x)^{n-1} \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + x \sum_{k = 0}^{n-1} {n-1 \choose k} x^k \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + \sum_{k = 0}^{n-1} {n-1 \choose k} x^{k+1} \\
&=& \sum_{k = 0}^{n-1} {n-1 \choose k} x^k + \sum_{k = 1}^{n} {n-1 \choose k-1} x^{k} \\
&=& \sum_{k = 0}^{n} {n-1 \choose k} x^k + \sum_{k = 0}^{n} {n-1 \choose k-1} x^{k} \\
&=& \sum_{k = 0}^{n} \left[{n-1 \choose k} + {n-1 \choose k-1}\right] x^{k}.
\end{eqnarray*}](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_6af59dfc59abaa3cff2d2625b18bf6bcab82cb7f_p1.png)
and now we equate matching coefficients to get
![\[{n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}\] \[{n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_5db4077b888cdb0fbb291c45f8c83c2eca510151_p1.png)
as advertised.
56. Vandermonde's identity
Vandermonde's identity says that, provided r does not exceed m or n,
![\[{m+n \choose r} = \sum_{k=0}^{r} {m \choose r-k}{n \choose k}.\] \[{m+n \choose r} = \sum_{k=0}^{r} {m \choose r-k}{n \choose k}.\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_c4129c9afa4345f940345e2002d79f0c8b7d20e2_p1.png)
56.1. Combinatorial proof
To pick r elements of an m+n element set, we have to pick some of them from the first m elements and some from the second n elements. Suppose we choose k elements from the last n; there are

different ways to do this, and

different ways to choose the remaining r-k from the first m. This gives (by the product rule)

ways to choose r elements from the whole set if we limit ourselves to choosing exactly k from the last n. The identity follow by summing over all possible values of k.
56.2. Algebraic proof
Here we use the fact that, for any sequences of coefficients {ai} and {bi},
![\[\left(\sum_{i=0}^{n} a_i x^i\right) \left(\sum_{i=0}^m b_i x^i\right)
= \sum_{i=0}^{m+n} \left(\sum_{j=0}^i a_j b_{i-j}\right) x^i.
\] \[\left(\sum_{i=0}^{n} a_i x^i\right) \left(\sum_{i=0}^m b_i x^i\right)
= \sum_{i=0}^{m+n} \left(\sum_{j=0}^i a_j b_{i-j}\right) x^i.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_e9e9a6c81222c63c923b208c1579bdcbfb960679_p1.png)
So now consider

and now equate terms with matching exponents.
Is this more enlightening than the combinatorial version? It depends on what kind of enlightnment you are looking for. In this case the combinatorial and algebraic arguments are counting essentially the same things in the same way, so it's not clear what if any advantage either has over the other. But in many cases it's easier to construct an algebraic argument than a combinatorial one, in the same way that it's easier to do arithmetic using standard grade-school algorithms than by constructing explicit bijections. On the other hand, a combinatorial argument may let you carry other things you know about some structure besides just its size across the bijection, giving you more insight into the things you are counting. The best course is probably to have both techniques in your toolbox.
57. Sums of binomial coefficients
What is the sum of all binomial coefficients for a given n? We can show
![\[\sum_{k=0}^{n} {n \choose k} = 2^n
\] \[\sum_{k=0}^{n} {n \choose k} = 2^n
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_caa67b38cbddc96f232d5687913caf2c89b7262f_p1.png)
combinatorially, by observing that adding up all subsets of an n-element set of all sizes is the same as counting all subsets. Alternatively, apply the binomial theorem to (1+1)n.
Here's another sum, with alternating sign. This is useful if you want to know how the even-k binomial coefficients compare to the odd-k binomial coefficients.
![\[\sum_{k=0}^{n} (-1)^k {n \choose k} = 0. \mbox{(Assuming $n \neq 0$.)}\] \[\sum_{k=0}^{n} (-1)^k {n \choose k} = 0. \mbox{(Assuming $n \neq 0$.)}\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_94e3dda017a3b0a7a4a63024450369ea7d3950ce_p1.png)
Proof: (1-1)n = 0n = 0 when n is nonzero. (When n is zero, the 0n part still works, since 00 = 1 = (0 choose 0)(-1)0.)
By now it should be obvious that
![\[\sum_{k=0}^{n} 2^k {n \choose k} = 3^n.\] \[\sum_{k=0}^{n} 2^k {n \choose k} = 3^n.\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_968427400ac83ee343e1dfd4676a7d73b7503d73_p1.png)
It's not hard to construct more examples of this phenomenon.
58. Application: the inclusion-exclusion formula
We've previously seen that |A∪B| = |A| + |B| - |A∩B|. The generalization of this fact from two to many sets is called the inclusion-exclusion formula and says
![\[
\left| \bigcup_{i=1}^n A_i \right|
=
\sum_{S \subseteq \{1 \ldots n\}, S \neq \emptyset}
(-1)^{|S|+1} \left| \bigcap_{j \in S} A_j \right|.
\] \[
\left| \bigcup_{i=1}^n A_i \right|
=
\sum_{S \subseteq \{1 \ldots n\}, S \neq \emptyset}
(-1)^{|S|+1} \left| \bigcap_{j \in S} A_j \right|.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_b31d64a6df9febd2592f88b45cc1a65bbccf2f36_p1.png)
This rather horrible expression means that to count the elements in the union of n sets A1 through An, we start by adding up all the individual sets |A1| + |A2| + ... |An|, then subtract off the overcount from elements that appear in two sets -|A1 ∩ A2| - |A1 ∩ A3| - ..., then add back the resulting undercount from elements that appear in three sets, and so on.
Why does this work? Consider a single element x that appears in k of the sets. We'll count it as +1 in (k choose 1) individual sets, as -1 in (k choose 2) pairs, +1 in (k choose 3) triples, and so on, adding up to
![\[
\sum_{i=1}^{k} (-1)^{k+1} {k \choose i}
= -\left(\sum_{i=1}^{k} (-1)^k {k \choose i}\right)
= -\left(\sum_{i=0}^{k} (-1)^k {k \choose i} - 1\right)
= -\left(0 - 1\right)
= 1.
\] \[
\sum_{i=1}^{k} (-1)^{k+1} {k \choose i}
= -\left(\sum_{i=1}^{k} (-1)^k {k \choose i}\right)
= -\left(\sum_{i=0}^{k} (-1)^k {k \choose i} - 1\right)
= -\left(0 - 1\right)
= 1.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_97bf9f4c20558d0fd9b9c19a60dd5074833299d9_p1.png)
59. Negative binomial coefficients
Though it doesn't make sense to talk about the number of k-subsets of a (-1)-element set, the binomial coefficient (n choose k) has a meaningful value for negative n, which works in the binomial theorem. We'll use the lower-factorial version of the definition:
![\[
{-n \choose k}
= (-n)_{k}/k!
= \left(\prod_{i=-n-k+1}^{-n} i\right) / k!
\] \[
{-n \choose k}
= (-n)_{k}/k!
= \left(\prod_{i=-n-k+1}^{-n} i\right) / k!
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_278f3392b3e91bd1d4be3a52889658ab1f32722f_p1.png)
Note we still demand that k∈ℕ; we are only allowed to do funny things with the upper index n.
So for example:
![\[
{-1 \choose k}
= (-1)_{k}/k!
= \left(\prod_{i=-1-k+1}^{-1} i\right) / k!
= \left(\prod_{i=-k}^{-1} i\right)/\left(\prod_{i=1}^{k} i\right)
= (-1)^k.
\] \[
{-1 \choose k}
= (-1)_{k}/k!
= \left(\prod_{i=-1-k+1}^{-1} i\right) / k!
= \left(\prod_{i=-k}^{-1} i\right)/\left(\prod_{i=1}^{k} i\right)
= (-1)^k.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_6ae7d2328d8a7cc2c96102f9f309cb175222230f_p1.png)
This means, for example, that
![\[
\frac{1}{1-z}
= (1-z)^{-1}
= \sum_{n=0}^{\infty} {-1 \choose n} 1^{-1-n} (-z)^n
= \sum_{n=0}^{\infty} (-1)^n (-z)^n
= \sum_{n=0}^{\infty} z^n.
\] \[
\frac{1}{1-z}
= (1-z)^{-1}
= \sum_{n=0}^{\infty} {-1 \choose n} 1^{-1-n} (-z)^n
= \sum_{n=0}^{\infty} (-1)^n (-z)^n
= \sum_{n=0}^{\infty} z^n.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_7fa7a1675232002cb0a37eec693a2c7b4d5e4a34_p1.png)
In computing this sum, we had to be careful which of 1 and -z got the n exponent and which got -1-n. If we do it the other way, we get
![\[
\frac{1}{1-z}
= (1-z)^{-1}
= \sum_{n=0}^{\infty} {-1 \choose n} 1^{n} (-z)^{-1-n}
= -\frac{1}{z} \sum_{n=0}^{\infty} \frac{1}{z^n}
\] \[
\frac{1}{1-z}
= (1-z)^{-1}
= \sum_{n=0}^{\infty} {-1 \choose n} 1^{n} (-z)^{-1-n}
= -\frac{1}{z} \sum_{n=0}^{\infty} \frac{1}{z^n}
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_68c8aaeab1aac9bb218c021e32e27e68da935c53_p1.png)
This turns out to actually be correct: applying the geometric series formula turns the last line into
![\[
-\frac{1}{z} \cdot \frac{1}{1-1/z}
= - \frac{1}{z - 1}
= \frac{1}{1-z},
\] \[
-\frac{1}{z} \cdot \frac{1}{1-1/z}
= - \frac{1}{z - 1}
= \frac{1}{1-z},
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_8d256361b47b128e342de1604423228e762985aa_p1.png)
but it's a lot less useful.
What happens for a larger upper index? One way to think about (-n)k is that we are really computing (n+k-1)k and then negating all the factors (which corresponds to multiplying the whole expression by (-1)k. So this gives us the identity
![\[
{-n \choose k}
= (-n)_{k}/k!
= (-1)^k (n+k-1)_{k} / k!
= (-1)^k {n+k-1 \choose k}.
\] \[
{-n \choose k}
= (-n)_{k}/k!
= (-1)^k (n+k-1)_{k} / k!
= (-1)^k {n+k-1 \choose k}.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_2d809e7436ad00c407689c06c39f8e046bd2adb3_p1.png)
So, for example,
![\[
\frac{1}{(1-z)^2}
= (1-z)^{-2}
= \sum_{n} {-2 \choose n} 1^{-2-n} (-z)^n
= \sum_{n} (-1)^n {n+1 \choose n} (-z)^n
= \sum_{n} (n+1) z^n.
\] \[
\frac{1}{(1-z)^2}
= (1-z)^{-2}
= \sum_{n} {-2 \choose n} 1^{-2-n} (-z)^n
= \sum_{n} (-1)^n {n+1 \choose n} (-z)^n
= \sum_{n} (n+1) z^n.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_070dd185a5a15baf5bfd1c377c8a3ec223a808da_p1.png)
These facts are useful when we look at GeneratingFunctions.
60. Fractional binomial coefficients
Yes, we can do fractional binomial coefficients, too. Exercise: Find the value of
![\[
{ 1/2 \choose n } = \frac{(1/2)_{n}}{n!}.
\] \[
{ 1/2 \choose n } = \frac{(1/2)_{n}}{n!}.
\]](/pinewiki/BinomialCoefficients?action=AttachFile&do=get&target=latex_eacc8d162da1eadb971df6dab2b32096105e1ace_p1.png)
61. Further reading
ConcreteMathematics §5.1–5.3 is an excellent source for information about all sorts of facts about binomial coefficients.
62. GeneratingFunctions
Contents
- Basics
- Some standard generating functions
- More operations on formal power series and generating functions
- Counting with generating functions
- Generating functions and recurrences
- Recovering coefficients from generating functions
- Asymptotic estimates
- Recovering the sum of all coefficients
- A recursive generating function
- Summary of operations on generating functions
- Variants
- Further reading
63. Basics
The short version: A generating function represents objects of weight n with zn, and adds all the objects you have up to get a sum a0z0 + a1z1 + a2z2 + ..., where each an counts the number of different objects of weight n. If you are very lucky (or constructed your set of objects by combining simpler sets of objects in certain straightforward ways) there will be some compact expression that is expands to this horrible sum but is easier to right down. Such compact expressions are called generating functions, and manipulating them algebraically gives an alternative to actually knowing HowToCount.
63.1. A simple example
We are given some initial prefixes for words: qu, s, and t; some vowels to put in the middle: a, i, and oi; and some suffixes: d, ff, and ck, and we want to calculate the number of words we can build of each length.
One way is to generate all 27 words6 and sort them by length:
sad sid tad tid quad quid sack saff sick siff soid tack taff tick tiff toid quack quaff quick quiff quoid soick soiff toick toiff quoick quoiff
This gives us 4 length-3 words, 12 length-4 words, 9 length-5 words, and 2 length-6 words. This is probably best done using a computer, and becomes expensive if we start looking at much larger lists.
An alternative is to solve the problem by judicious use of algebra. Pretend that each of our letters is actually a variable, and that when we concatenate qu, oi, and ck to make quoick, we are really multiplying the variables using our usual notation. Then we can express all 27 words as the product (qu+s+t)(a+i+oi)(d+ff+ck). But we don't care about the exact set of words, we just want to know how many we get of each length.
So now we do the magic trick: we replace every variable we've got with a single variable z. For example, this turns quoick into zzzzzz = z6, so we can still find the length of a word by reading off the exponent on z. But we can also do this before we multiply everything out, getting

We can now read off the number of words of each length directly off the coefficients of this polynomial.
63.2. Why this works
In general, what we do is replace any object of weight 1 with z. If we have an object with weight n, we think of it as n weight-1 objects stuck together, i.e., zn. Disjoint unions are done using addition as in simple counting: z+z2 represents the choice between a weight-1 object and a weight-2 object (which may have been built out of 2 weight-1 objects), while 12z4 represents a choice between 12 different weight-4 objects. The trick is that when we multiply two expressions like this, whenever two values zk and zl collide, the exponents add to give a new value zk+l representing a new object with total weight k+l, and if we have something more complex like (nzk)(mzl), then the coefficient multiply to give (nm)zk+l different weight (k+l) objects.
For example, suppose we want to count the number of robots we can build given 5 choices of heads, each of weight 2, and 6 choices of bodies, each of weight 5. We represent the heads by 5z2 and the bodies by 6z5. When we multiply these expressions together, the coefficients multiply (which we want, by the product rule) and the exponents add: we get 5z2⋅6z5 = 30z7 or 30 robots of weight 7 each.
The real power comes in when we consider objects of different weights. If we add to our 5 weight-2 robot heads two extra-fancy heads of weight 3, and compensate on the body side with three new lightweight weight-4 bodies, our new expression is (5z2+2z3)(3z4+6z5) = 15z6+36z7+12z8, giving a possible 15 weight-6 robots, 36 weight-7 robots, and 12 weight-8 robots. The rules for multiplying polynomials automatically tally up all the different cases for us.
This trick even works for infinitely-long polynomials that represent infinite series (such "polynomials" are called formal power series). Even though there might be infinitely many ways to pick three natural numbers, there are only finitely many ways to pick three natural numbers whose sum is 37. By computing an appropriate formal power series and extracting the coefficient from the z37 term, we can figure out exactly how many ways there are. This works best, of course, when we don't have to haul around an entire infinite series, but can instead represent it by some more compact function whose expansion gives the desired series. Such a function is called a generating function, and manipulating generating functions can be a powerful alternative to creativity in making combinatorial arguments.
63.3. Formal definition
Given a sequence a0,a1,a2,..., its generating function F(z) is given by the sum
![\[
F(z) = \sum_{i=0}^{\infty} a_i z^i.
\] \[
F(z) = \sum_{i=0}^{\infty} a_i z^i.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_9f2e1d7af7183fae2fc7a422e6aca768635a5392_p1.png)
A sum in this form is called a formal power series. It is "formal" in the sense that we don't necessarily plan to actually compute the sum, and are instead using the string of zi terms as a long rack to store coefficients on.
In some cases, the sum has a more compact representation. For example, we have
![\[
\frac{1}{1-z} = \sum_{i=0}^{\infty} z^i,
\] \[
\frac{1}{1-z} = \sum_{i=0}^{\infty} z^i,
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_efb5d1a3271394a7c4207ec4dc669e849f6ff84f_p1.png)
so 1/(1-z) is the generating function for the sequence 1,1,1,.... This may let us manipulate this sequence conveniently by manipulating the generating function.
Here's a simple case. If F(z) generates some sequence ai, what does sequence bi does F(2z) generate? The i-th term in the expansion of F(2z) will be ai(2z)i = ai 2i zi, so we have bi = 2i ai. This means that the sequence 1,2,4,8,16,... has generating function 1/(1-2z). In general, if F(z) represents ai, then F(cz) represents ciai.
What else can we do to F? One useful operation is to take its derivative with respect to z. We then have
![\[
\frac{d}{dz} F(z)
= \sum_{i=0}^{\infty} a_i \frac{d}{dz} z^i
= \sum_{i=0}^{\infty} a_i i z^{i-1}.
\] \[
\frac{d}{dz} F(z)
= \sum_{i=0}^{\infty} a_i \frac{d}{dz} z^i
= \sum_{i=0}^{\infty} a_i i z^{i-1}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_d363de1dff08160b543057c866cdc691366e03a3_p1.png)
This almost gets us the representation for the series i ai, but the exponents on the z's are off by one. But that's easily fixed:
![\[
z \frac{d}{dz} F(z) = \sum_{i=0}^{\infty} a_i i z^i.
\] \[
z \frac{d}{dz} F(z) = \sum_{i=0}^{\infty} a_i i z^i.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_853f856447390ead0bf160e410cd355cb0a8373f_p1.png)
So the sequence 0,1,2,3,4,... has generating function
![\[
z \frac{d}{dz} \frac{1}{1-z} = \frac{z}{(1-z)^2},
\] \[
z \frac{d}{dz} \frac{1}{1-z} = \frac{z}{(1-z)^2},
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_f146b504c6081af312f05ae74595f352fdf37b43_p1.png)
and the sequence of squares 0,1,4,9,16,... has generating function
![\[
z \frac{d}{dz} \frac{z}{(1-z)^2}
= \frac{z}{(1-z)^2} + \frac{2z^2}{(1-z)^3}.
\] \[
z \frac{d}{dz} \frac{z}{(1-z)^2}
= \frac{z}{(1-z)^2} + \frac{2z^2}{(1-z)^3}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_7232d3b64c89c43105d4f5d24219091d5d3792a6_p1.png)
As you can see, some generating functions are prettier than others.
(We can also use integration to divide each term by i, but the details are messier.)
Another way to get the sequence 0,1,2,3,4,... is to observe that it satisfies the recurrence:
a0 = 0
an+1 = an + 1 (∀n∈ℕ)
A standard trick in this case is to multiply each of the ∀i bits by zn, sum over all n, and see what happens. This gives ∑ an+1zn = ∑ anzn + ∑ zn = ∑ anzn + 1/(1-z). The first term on the right-hand side is the generating function for an, which we can call F(z) so we don't have to keep writing it out. The second term is just the generating function for 1,1,1,1,1,... . But what about the left-hand side? This is almost the same as F(z), except the coefficients don't match up with the exponents. We can fix this by dividing F(z) by z, after carefully subtracting off the a0 term:

So this gives the equation (F(z) - a0)/z = F(z) + 1/(1-z). Since a0 = 0, we can rewrite this as F(z)/z = F(z) + 1/(1-z). A little bit of algebra turns this into F(z) - zF(z) = z/(1-z) or F(z) = z/(1-z)2.
Yet another way to get this sequence is construct a collection of objects with a simple structure such that there are exactly n objects with weight n. One way to do this is to consider strings of the form a+b* where we have at least one a followed by zero or more b's. This gives n strings of length n, because we get one string for each of 1..n a's we can put in (an example would be abb, aab, and aaa for n=3). We can compute the generating function for this set because to generate each string we must pick in order:
- One initial a. Generating function = z.
- Zero or more a's. Generating function = 1/(1-z).
- Zero or more b's. Generating function = 1/(1-z).
Taking the product of these gives z/(1-z)2, as before.
This trick is useful in general; if you are given a generating function F(z) for an, but want a generating function for bn = ∑k≤n ak, allow yourself to pad each weight-k object out to weight n in exactly one way using n-k junk objects, i.e. multiply F(z) by 1/(1-z).
64. Some standard generating functions
Here is a table of some of the most useful generating functions.

Of these, the first is the most useful to remember (it's also handy for remembering how to sum geometric series). All of these equations can be proven using the binomial theorem.
65. More operations on formal power series and generating functions
Let F(z) = ∑i aizi and G(z) = ∑i bizi. Then their sum F(z)+G(z) = ∑i (ai+bi)zi is the generating function for the sequence (ai+bi). What is their product F(z)G(z)?
To compute the i-th term of F(z)G(z), we have to sum over all pairs of terms, one from F and one from G, that produce a zi factor. Such pairs of terms are precisely those that have exponents that sum to i. So we have
![\[F(z)G(z) = \sum_{i=0}^{\infty} \left(\sum_{j=0}^{i} a_j b_{j-i}\right) z^i.\] \[F(z)G(z) = \sum_{i=0}^{\infty} \left(\sum_{j=0}^{i} a_j b_{j-i}\right) z^i.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_ea6d2381e4231b014dd882d9a5457c036c12f22c_p1.png)
As we've seen, this equation has a natural combinatorial interpretation. If we interpret the coefficient ai on the i-th term of F(z) as counting the number of "a-things" of weight i, and the coefficient bi as the number of "b-things" of weight i, then the i-th coefficient of F(z)G(z) counts the number of ways to make a combined thing of total weight i by gluing together an a-thing and a b-thing.
As a special case, if F(z)=G(z), then the i-th coefficient of F(z)G(z) = F2(z) counts how many ways to make a thing of total weight i using two "a-things", and Fn(z) counts how many ways (for each i) to make a thing of total weight i using n "a-things". This gives us an easy combinatorial proof of a special case of the binomial theorem:
![\[(1+x)^n = \sum_{i=0}^{\infty} {n \choose i} x^i.\] \[(1+x)^n = \sum_{i=0}^{\infty} {n \choose i} x^i.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_5810a1fd8e28f4ed1ec59d80f3424eca23ad51f4_p1.png)
Think of the left-hand side as the generating function F(x) = 1+x raised to the n-th power. F by itself says that you have a choice between one weight-0 object or one weight-1 object. On the right-hand side the i-th coefficient counts how many ways you can put together a total of i weight-1 objects given n to choose from—so it's n choose i.
66. Counting with generating functions
The product formula above suggests that generating functions can be used to count combinatorial objects that are built up out of other objects, where our goal is to count the number of objects of each possible non-negative integer "weight" (we put "weight" in scare quotes because we can make the "weight" be any property of the object we like, as long as it's a non-negative integer—a typical choice might be the size of a set, as in the binomial theorem example above). There are five basic operations involved in this process; we've seen two of them already, but will restate them here with the others.
Throughout this section, we assume that F(z) is the generating function counting objects in some set A and G(z) the generating function counting objects in some set B.
66.1. Disjoint union
Suppose C = A∪B and A and B are disjoint. Then the generating function for objects in C is F(z)+G(z).
Example: Suppose that A is the set of all strings of zero or more letters x, where the weight of a string is just its length. Then F(z) = 1/(1-z), since there is exactly one string of each length and the coefficient ai on each zi is always 1. Suppose that B is the set of all strings of zero or more letters y and/or z, so that G(z) = 1/(1-2z) (since there are now 2i choices of length-i strings). The set C of strings that are either (a) all x's or (b) made up of y's, z's, or both, has generating function F(z)+G(z) = 1/(1-z) + 1/(1-2z).
66.2. Cartesian product
Now let C = A×B, and let the weight of a pair (a,b)∈C be the sum of the weights of a and b. Then the generating function for objects in C is F(z)G(z).
Example: Let A be all-x strings and B be all y or z strings, as in the previous example. Let C be the set of all strings that consist of zero or more x's followed by zero or more y's and/or z's. Then the generating function for C is F(z)G(z) = 1/((1-z)(1-2z)).
66.3. Repetition
Now let C consists of all finite sequences of objects in A, with the weight of each sequence equal to the sum of the weights of its elements (0 for an empty sequence). Let H(z) be the generating function for C. From the preceding rules we have
H = 1 + F + F2 + F3 + ... = 1/(1-F).
This works best when H(0) = 0; otherwise we get infinitely many weight-0 sequences. It's also worth noting that this is just a special case of substitution (see below), where our "outer" generating function is 1/(1-z).
66.3.1. Example: (0|11)*
Let A = { 0, 11 }, and let C be the set of all sequences of zeroes and ones where ones occur only in even-length runs. Then the generating function for A is z+z2 and the generating function for C is 1/(1-z-z2). We can extract exact coefficients from this generating function using the techniques below.
66.3.2. Example: sequences of positive integers
Suppose we want to know how many different ways there are to generate a particular integer as a sum of positive integers. For example, we can express 4 as 4, 3+1, 2+2, 2+1+1, 1+1+1+1, 1+1+2, 1+2+1, or 1+3, giving 8 different ways.
We can solve this problem using the repetition rule. Let F = z/(1-z) generate all the positive integers. Then

We can get exact coefficients by observing that

This means that there is 1 way to express 0 (the empty sum), and 2n-1 ways to express any larger value n (e.g. 24-1 = 8 ways to express 4).
Once we know what the right answer is, it's not terribly hard to come up with a combinatorial explanation. The quantity 2n-1 counts the number of subsets of an (n-1)-element set. So imagine that we have n-1 places and we mark some subset of them, plus add an extra mark at the end; this might give us a pattern like XX-X. Now for each sequence of places ending with a mark we replace it with the number of places (e.g. XX-X = 1,1,2, X--X-X---X = 1,3,2,4). Then the sum of the numbers we get is equal to n, because it's just counting the total length of the sequence by dividing it up at the marks and the adding the pieces back together. The value 0 doesn't fit this pattern (we can't put in the extra mark without getting a sequence of length 1), so we have 0 as a special case again.
If we are very clever, we might come up with this combinatorial explanation from the beginning. But the generating function approach saves us from having to be clever.
66.4. Pointing
This operation is a little tricky to describe. Suppose that we can think of each weight-k object in A as consisting of k items, and that we want to count not only how many weight-k objects there are, but how many ways we can produce a weight-k object where one of its k items has a special mark on it. Since there are k different items to choose for each weight-k object, we are effectively multiplying the count of weight-k objects by k. In generating function terms, we have
- H(z) = z d/dz F(z).
Repeating this operation allows us to mark more items (with some items possibly getting more than one mark). If we want to mark n distinct items in each object (with distinguishable marks), we can compute
H(z) = zn dn/dzn F(z),
where the repeated derivative turns each term ai zi into aii(i-1)(i-2)...(i-n+1) zi-n and the zn factor fixes up the exponents. To make the marks indistinguishable (i.e., we don't care what order the values are marked in), divide by n! to turn the extra factor into (i choose n).
(If you are not sure how to take a derivative, look at HowToDifferentiate.)
Example: Count the number of finite sequences of zeroes and ones where exactly two digits are underlined. The generating function for { 0, 1 } is 2z, so the generating function for sequences of zeros and ones is F = 1/(1-2z) by the repetition rule. To mark two digits with indistinguishable marks, we need to compute
![\[\frac{1}{2} z^2 \frac{d^2}{dz^2} \frac{1}{1-2z}
= \frac{1}{2} z^2 \frac{d}{dz} \frac{2}{(1-2z)^2}
= \frac{1}{2} z^2 \frac{8}{(1-2z)^3}
= \frac{4z^2}{(1-2z)^3}.\] \[\frac{1}{2} z^2 \frac{d^2}{dz^2} \frac{1}{1-2z}
= \frac{1}{2} z^2 \frac{d}{dz} \frac{2}{(1-2z)^2}
= \frac{1}{2} z^2 \frac{8}{(1-2z)^3}
= \frac{4z^2}{(1-2z)^3}.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_720937f630906e93e000994ecd99edd595fd6c0a_p1.png)
66.5. Substitution
Suppose that the way to make a C-thing is to take a weight-k A-thing and attach to each its k items a B-thing, where the weight of the new C-thing is the sum of the weights of the B-things. Then the generating function for C is the composition F(G(z)).
Why this works: suppose we just want to compute the number of C-things of each weight that are made from some single specific weight-k A-thing. Then the generating function for this quantity is just (G(z))k. If we expand our horizons to include all ak weight-k A-things, we have to multiply by ak to get ak (G(z))k. If we further expand our horizons to include A-things of all different weights, we have to sum over all k:
![\[
\sum_{k=0}^{\infty} a_k (G(z))^k.
\] \[
\sum_{k=0}^{\infty} a_k (G(z))^k.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_daa5947fc60dc9fd77edc812581eed6047fd27f2_p1.png)
But this is just what we get if we start with F(z) and substitute G(z) for each occurrence of z, i.e. if we compute F(G(z)).
66.5.1. Example: bit-strings with primes
Suppose we let A be all sequences of zeroes and ones, with generating function F(z) = 1/(1-2z). Now suppose we can attach a single or double prime to each 0 or 1, giving 0' or 0'' or 1' or 1'', and we want a generating function for the number of distinct primed bit-strings with n attached primes. The set { prime, prime-prime } has generating function G(z)=z+z2, so the composite set has generating function F(z) = 1/(1-2(z+z2)) = 1/(1-2z-2z2).
66.5.2. Example: (0|11)* again
The previous example is a bit contrived. Here's one that's a little more practical, although it involves a brief digression into multivariate generating functions. A multivariate generating function F(x,y) generates a series ∑ij aij xiyj, where aij counts the number of things that have i x's and j y's. (There is also the obvious generalization to more than two variables). Consider the multivariate generating function for the set { 0, 1 }, where x counts zeroes and y counts ones: this is just x+y. The multivariate generating function for sequences of zeroes and ones is 1/(1-x-y) by the repetition rule. Now suppose that each 0 is left intact but each 1 is replaced by 11, and we want to count the total number of strings by length, using z as our series variable. So we substitute z for x and z2 (since each one turns into a string of length 2) for y, giving 1/(1-z-z2). This gives another way to get the generating function for strings built by repeating 0 and 11.
67. Generating functions and recurrences
What makes generating functions particularly useful for algorithm analysis is that they directly solve recurrences of the form T(n) = a T(n-1) + b T(n-2) + f(n) (or similar recurrences with more T terms on the right-hand side), provided we have a generating function F(z) for f(n). The idea is that there exists some generating function G(z) that describes the entire sequence of values T(0),T(1),T(2),..., and we just need to solve for it by restating the recurrence as an equation about G. The left-hand side will just turn into G. For the right-hand side, we need to shift T(n-1) and T(n-2) to line up right, so that the right-hand side will correctly represent the sequence T(0),T(1),aT(0)+aT(1)+F(2), etc. It's not hard to see that the generating function for the sequence 0,T(0),T(1),T(2),... (corresponding to the T(n-1) term) is just zG(z), and similarly the sequence 0,0,T(1),T(2),T(3),... (corresponding to the T(n-2) term) is z2G(z). So we have (being very careful to subtract out extraneous terms at for i=0 and i=1):
G = az(G - T(0)) + bz2G + (F - f(0) - zf(1)) + T(0) + zT(1),
and after expanding F we can in principle solve this for G as a function of z.
67.1. Example: A Fibonacci-like recurrence
Let's take a concrete example. The Fibonacci-like recurrence
- T(n) = T(n-1) + T(n-2), T(0) = 1, T(1) = 1,
becomes
G = (zG - z) + z2G + 1 + z.
(here F = 0).
Solving for G gives
G = 1/(1 - z - z2).
Unfortunately this is not something we recognize from our table, although it has shown up in a couple of examples. (Exercise: Why does the recurrence T(n) = T(n-1) + T(n-2) count the number of strings built from 0 and 11 of length n?) In the next section we show how to recover a closed-form expression for the coefficients of the resulting series.
68. Recovering coefficients from generating functions
There are basically three ways to recover coefficients from generating functions:
- Recognize the generating function from a table of known generating functions, or as a simple combination of such known generating functions. This doesn't work very often but it is possible to get lucky.
To find the k-th coefficient of F(z), compute the k-th derivative dk/dzk F(z) and divide by k! to shift ak to the z0 term. Then substitute 0 for z. For example, if F(z) = 1/(1-z) then a0 = 1 (no differentiating), a1 = 1/(1-0)2 = 1, a2 = 1/(1-0)3 = 1, etc. This usually only works if the derivatives have a particularly nice form or if you only care about the first couple of coefficients (it's particularly effective if you only want a0).
If the generating function is of the form 1/Q(z), where Q is a polynomial with Q(0)≠0, then it is generally possible to expand the generating function out as a sum of terms of the form Pc/(1-z/c) where c is a root of Q (i.e. a value such that Q(c) = 0). Each denominator Pc will be a constant if c is not a repeated root; if c is a repeated root, then Pc can be a polynomial of degree up to one less than the multiplicity of c. We like these expanded solutions because we recognize 1/(1-z/c) = ∑i c-i zi, and so we can read off the coefficients ai generated by 1/Q(z) as an appropriately weighted some of c1-i, c2-i, etc., where the cj range over the roots of Q.
Example: Take the generating function G = 1/(1-z-z2). We can simplify it by factoring the denominator: 1-z-z2 = (1-az)(1-bz) where 1/a and 1/b are the solutions to the equation 1-z-z2=0; in this case a = (1+√5)/2, which is approximately 1.618 and b = (1-√5)/2, which is approximately -0.618. It happens to be the case that we can always expand 1/P(z) as A/(1-az) + B(1-bz) for some constants A and B whenever P is a degree 2 polynomial with constant coefficient 1 and distinct roots a and b, so
- G = A/(1-az) + B/(1-bz),
and here we can recognize the right-hand side as the sum of the generating functions for the sequences A⋅ai and B⋅bi. The A⋅ai term dominates, so we have that T(n) = Theta(an), where a is approximately 1.618. We can also solve for A and B exactly to find an exact solution if desired.
A rule of thumb that applies to recurrences of the form T(n) = a1T(n-1) + a2T(n-2) + ... ak T(n-k) + f(n) is that unless f is particularly large, the solution is usually exponential in 1/x, where x is the smallest root of the polynomial 1 - a1z - a2z2 ... - ak zk. This can be used to get very quick estimates of the solutions to such recurrences (which can then be proved without fooling around with generating functions).
Exercise: What is the exact solution if T(n) = T(n-1) + T(n-2) + 1? Or if T(n) = T(n-1) + T(n-2) + n?
68.1. Partial fraction expansion and Heaviside's cover-up method
There is a nice trick for finding the numerators in a partial fraction expansion. Suppose we have
![\[\frac{1}{(1-az)(1-bz)} = \frac{A}{1-az} + \frac{B}{1-bz}.\] \[\frac{1}{(1-az)(1-bz)} = \frac{A}{1-az} + \frac{B}{1-bz}.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_4ab8cfbf5db7de953e4a6dc6fee89c2aa2f952ce_p1.png)
Multiply both sides by 1-az to get
![\[\frac{1}{1-bz} = A + \frac{B(1-az)}{1-bz}.\] \[\frac{1}{1-bz} = A + \frac{B(1-az)}{1-bz}.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_1971f711206a6129e1e4ed310fc30791cea5a8b1_p1.png)
Now plug in z = 1/a to get
![\[\frac{1}{1-b/a} = A + 0.\] \[\frac{1}{1-b/a} = A + 0.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_98e7c56b8322445b738cc90287f09bf1b6e73b32_p1.png)
We can immediately read off A. Similarly, multiplying by 1-bz and then setting 1-bz to zero gets B. The method is known as the "cover-up method" because multiplication by (1-az) can be simulated by covering up (1-az) in the denominator of the left-hand side and all the terms that don't have (1-az) in the denominator in the right hand side.
The cover-up method will work in general whenever there are no repeated roots, even if there are many of them; the idea is that setting 1-qz to zero knocks out all the terms on the right-hand side but one. With repeated roots we have to worry about getting numerators that aren't just a constant, so things get more complicated. We'll come back to this case below.
68.1.1. Example: A simple recurrence
Suppose f(0) = 0, f(1) = 1, and for n≥2, f(n) = f(n-1) + 2f(n-2). Multiplying these equations by zn and summing over all n gives a generating function
![\[
F(z) = \sum_{n=0}{\infty} f(n) z^n = 0\cdot z^0 + 1\cdot z^1 + \sum_{n=2}^{\infty} f(n-1) z^n + \sum_{n=2}^{\infty} 2f(n-2) z^n.
\] \[
F(z) = \sum_{n=0}{\infty} f(n) z^n = 0\cdot z^0 + 1\cdot z^1 + \sum_{n=2}^{\infty} f(n-1) z^n + \sum_{n=2}^{\infty} 2f(n-2) z^n.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_a372e2769c0f7dd4a068f0498ed0bb0183687e8d_p1.png)
With a bit of tweaking, we can get rid of the sums on the RHS by converting them into copies of F:

Now solve for F(z) to get  , where we need to solve for A and B.
, where we need to solve for A and B.
We can do this directly, or we can use the cover-up method. The cover-up method is easier. Setting z = -1 and covering up 1+z gives A = 1/(1-2(-1)) = 1/3. Setting z = 1/2 and covering up 1-2z gives B = 1/(1+z) = 1/(1+1/2) = 2/3. So we have

So we have f(0) = 0 and, for n≥1,  . It's not hard to check that this gives the same answer as the recurrence.
. It's not hard to check that this gives the same answer as the recurrence.
68.1.2. Example: Coughing cows
Let's count the number of strings of each length of the form (M)*(O|U)*(G|H|K)* where (x|y) means we can use x or y and * means we can repeat the previous parenthesized expression 0 or more times (see Regular_expression).
We start with a sequence of 0 or more M's. The generating function for this part is our old friend 1/(1-z). For the second part, we have two choices for each letter, giving 1/(1-2z). For the third part, we have 1/(1-3z). Since each part can be chosen independently of the other two, the generating function for all three parts together is just the product:
![\[
\frac{1}{(1-z)(1-2z)(1-3z)}.
\] \[
\frac{1}{(1-z)(1-2z)(1-3z)}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_874c9eb901e26f2e752da076f7f57f825398bf99_p1.png)
Let's use the cover-up method to convert this to a sum of partial fractions. We have

So the exact number of length-n sequences is (1/2) - 4⋅2n + (9/2)⋅3n. We can check this for small n:
n |
Formula |
Strings |
0 |
1/2 - 4 + 9/2 = 1 |
() |
1 |
1/2 - 8 + 27/2 = 6 |
M, O, U, G, H, K |
2 |
1/2 - 16 + 81/2 = 25 |
MM, MO, MU, MG, MH, MK, OO, OU, OG, OH, OK, UO, UU, UG, UH, UK, GG, GH, GK, HG, HH, HK, KG, KH, KK |
3 |
1/2 - 32 + 243/2 = 90 |
(exercise) ☺ |
68.1.3. Example: A messy recurrence
Let's try to solve the recurrence T(n) = 4T(n-1) + 12T(n-2) + 1 with T(0) = 0 and T(1) = 1.
Let F = ∑ T(n)zn.
Summing over all n gives

Solving for F then gives

We want to solve this using partial fractions, so we need to factor (1-4z-12z²) = (1+2z)(1-6z). This gives

From this we can immediately read off the value of T(n) for n≥2:

Let's check this against the solutions we get from the recurrence itself:
n |
T(n) |
0 |
0 |
1 |
1 |
2 |
1+4⋅1+12⋅0 = 5 |
3 |
1+4⋅5+12⋅1 = 33 |
4 |
1+4⋅33+12⋅5 = 193 |
We'll try n=3, and get T(3) = (3/20)⋅216 + 8/12 - 1/15 = (3⋅3⋅216 + 40 - 4)/60 = (1944 + 40 - 4)/60 = 1980/60 = 33.
To be extra safe, let's try T(2) = (3/20)⋅36 - 4/12 - 1/15 = (3⋅3⋅36 - 20 - 4)/60 = (324 - 20 - 4)/60 = 300/60 = 5. This looks good too.
The moral of this exercise? Generating functions can solve ugly-looking recurrences exactly, but you have to be very very careful in doing the math.
68.2. Partial fraction expansion with repeated roots
Let an = 2an-1 + n, with some constant a0. Find a closed-form formula for an.
As a test, let's figure out the first few terms of the sequence:
a0 = a0 |
a1 = 2a0 + 1 |
a2 = 4a0 + 2 + 2 = 4a0+4 |
a3 = 8a0 + 8 + 3 = 8a0+11 |
a4 = 16a0 + 22 + 4 = 16a0+26 |
The a0 terms look nice (they're 2na0), but the 0, 1, 4, 11, 26 sequence doesn't look like anything familiar. So we'll find the formula the hard way.
First we convert the recurrence into an equation over generating functions and solve for the generating function F:

Observe that the right-hand term gives us exactly the 2na0 terms we expected, since 1/(1-2z) generates the sequence 2n. But what about the left-hand term? Here we need to apply a partial-fraction expansion, which is simplified because we already know how to factor the denominator but is complicated because there is a repeated root.
We can now proceed in one of two ways: we can solve directly for the partial fraction expansion, or we can use an extended version of Heaviside's cover-up method that handles repeated roots using differentiation. We'll start with the direct method.
68.2.1. Solving for the PFE directly
Write
![\[\frac{1}{(1-z)^2(1-2z)} = \frac{A}{(1-z)^2} + \frac{B}{1-2z}\]. \[\frac{1}{(1-z)^2(1-2z)} = \frac{A}{(1-z)^2} + \frac{B}{1-2z}\].](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_f35e7800ac17785da9f341eb4b60d24897d97ca2_p1.png)
We expect B to be a constant and A to be of the form A1z + A0.
To find B, use the technique of multiplying by 1-2z and setting z=1/2:
![\[\frac{1}{(1-\frac{1}{2})^2} = \frac{A\cdot 0}{(1-z)^2} + B,\] \[\frac{1}{(1-\frac{1}{2})^2} = \frac{A\cdot 0}{(1-z)^2} + B,\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_fc87140a8fdd8610ad81f5017f44b1ecbc98592b_p1.png)
so B = 1/(1-1/2)2 = 1/(1/4) = 4.
We can't do this for A, but we can solve for it after substituting in B = 4:

So we have the expansion
![\[\frac{1}{(1-z)^2(1-2z)} = \frac{2z-3}{(1-z)^2} + \frac{4}{1-2z},\] \[\frac{1}{(1-z)^2(1-2z)} = \frac{2z-3}{(1-z)^2} + \frac{4}{1-2z},\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_16893e122984666c6004dec14a6c6580da9e10b5_p1.png)
from which we get

If we remember that 1/(1-z)2 generates the sequence xn = n+1 and 1/(1-2z) generates xn = 2n, then we can quickly read off the solution (for large n):
![\[a_n = 2(n-1) - 3n + 4\cdot 2^{n-1} + a_0\cdot 2^n
= 2^n a_0 + 2^{n+1} - 2 - n\] \[a_n = 2(n-1) - 3n + 4\cdot 2^{n-1} + a_0\cdot 2^n
= 2^n a_0 + 2^{n+1} - 2 - n\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_f17c3c6e808dd1d11a3cbc8a03999606f5452348_p1.png)
which we can check by plugging in particular values of n and comparing it to the values we got by iterating the recurrence before.
The reason for the "large n" caveat is that z2/(1-z)2 doesn't generate precisely the sequence xn = n-1, since it takes on the values 0, 0, 1, 2, 3, 4, ... instead of -1, 0, 1, 2, 3, 4, ... . Similarly, the power series for z/(1-2z) does not have the coefficient 2n-1 = 1/2 when n = 0. Miraculously, in this particular example the formula works for n = 0, even though it shouldn't: 2(n-1) is -2 instead of 0, but 4·2n-1 is 2 instead of 0, and the two errors cancel each other out.
68.2.2. Solving for the PFE using the extended cover-up method
It is also possible to extend the cover-up method to handle repeated roots. Here we choose a slightly different form of the partial fraction expansion:
![\[
\frac{1}{(1-z)^2 (1-2z)} = \frac{A}{(1-z)^2} + \frac{B}{1-z} + \frac{C}{1-2z}.
\] \[
\frac{1}{(1-z)^2 (1-2z)} = \frac{A}{(1-z)^2} + \frac{B}{1-z} + \frac{C}{1-2z}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_4db57c7cdc06797b608a81d237959c746fbaf713_p1.png)
Here A, B, and C are all constants. We can get A and C by the cover-up method, where for A we multiply both sides by (1-z)² before setting z=1; this gives A = 1/(1-2) = -1 and C = 1/(1-½)² = 4. For B, if we multiply both sides by (1-z) we are left with A/(1-z) on the right-hand side and a (1-z) in the denominator on the left-hand side. Clearly setting z = 1 in this case will not help us.
The solution is to first multiply by (1-z)² as before but then take a derivative:

Now if we set z = 1, every term on the right-hand side except -B becomes 0, and we get -B = 2/(1-2)² or B = -2.
Plugging A, B, and C into our original formula then gives
![\[
\frac{1}{(1-z)^2(1-2z)} = \frac{-1}{(1-z)^2} + \frac{-2}{1-z} + \frac{4}{1-2z}.
\] \[
\frac{1}{(1-z)^2(1-2z)} = \frac{-1}{(1-z)^2} + \frac{-2}{1-z} + \frac{4}{1-2z}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_b739605938588ba9f015e48e918faac821f66ce6_p1.png)
and thus
![\[
F = \frac{z}{(1-z)^2(1-2z)} + \frac{a_0}{1-2z} = z\left(\frac{-1}{(1-z)^2} + \frac{-2}{1-z} + \frac{4}{1-2z}\right) + \frac{a_0}{1-2z}.
\] \[
F = \frac{z}{(1-z)^2(1-2z)} + \frac{a_0}{1-2z} = z\left(\frac{-1}{(1-z)^2} + \frac{-2}{1-z} + \frac{4}{1-2z}\right) + \frac{a_0}{1-2z}.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_45def09d7387530927efe9f30d1ca343878d6b37_p1.png)
From this we can read off (for large n):
![\[
a_n = 4\cdot 2^{n-1} - n - 2 + a_0 \cdot 2^n = 2^{n+1} + 2^n a_0 - n - 2.
\] \[
a_n = 4\cdot 2^{n-1} - n - 2 + a_0 \cdot 2^n = 2^{n+1} + 2^n a_0 - n - 2.
\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_a593b77c32c8014a0a4a2885d3982574a85e8d52_p1.png)
We believe this because it looks like the solution we already got.
69. Asymptotic estimates
We can simplify our life considerably if we only want an asymptotic estimate of an (see AsymptoticNotation). The basic idea is that if an is non-negative for sufficiently large n and ∑ anzn converges for some fixed value z, then an must be o(z-n) in the limit. (Proof: otherwise, anzn is at least a constant for infinitely many n, giving a divergent sum.) So we can use the radius of convergence of a generating function F(z), defined as the largest value r such that F(z) is defined for all (complex) z with |z| < r, to get a quick estimate of the growth rate of F's coefficients: whatever they do, we have an = O(r-n).
For generating functions that are rational functions (ratios of polynomials), we can use the partial fraction expansion to do even better. First observe that for F(z) = ∑ fizn = 1/(1-az)k, we have fn = (k+n-1 choose n) an = ((n+k-1),,(k-1)/(k-1)!) an = Θ(an nk-1). Second, observe that the denominator is irrelevant: if 1/(1-az)k = Θ(an nk-1) then bzm/(1-az)k-1 = b Θ(an-m (n-m)k-1) = b a-m (1-m/n)k-1 Θ(an nk-1) = Θ(an nk-1), because everything outside the Θ disappears into the constant for sufficiently large n. Finally, observe that in a partial fraction expansion, the term 1/(1-az)k with the largest coefficient a (if there is one) wins in the resulting asymptotic sum: Θ(an) + Θ(bn) = Θ(an) if |a| > |b|. So we have:
- Theorem
Let F(z) = ∑ fnzn = P(z)/Q(z) where P and Q are polynomials in z. If Q has a root r with multiplicity k, and all other roots s of Q satisfy |r| < |s|, then fn = Θ((1/r)n nk-1).
The requirement that r is a unique minimal root of Q is necessary; for example, F(z) = 2/(1-z²) = 1/(1-z) + 1/(1+z) generates the sequence 0, 2, 0, 2, ..., which is not Θ(1) because of all the zeros; here the problem is that 1-z² has two roots with the same absolute value, so for some values of n it is possible for them to cancel each other out.
A root in the denominator of a rational function F is called a pole. So another way to state the theorem is that the asymptotic value of the coefficients of a rational generating function is determined by the smallest pole.
More examples:
F(z) |
Smallest pole |
Asymptotic value |
1/(1-z) |
1 |
Θ(1) |
1/(1-z)² |
1, multiplicity 2 |
Θ(n) |
1/(1-z-z²) |
(√5-1)/2 = 2/(1+√5) |
Θ(((1+√5)/2)n) |
1/((1-z)(1-2z)(1-3z)) |
1/3 |
Θ(3n) |
(z+z²(1-z))/(1-4z-12z²) |
1/6 |
Θ(6n) |
1/((1-z)²(1-2z)) |
1/2 |
Θ(2n) |
In each case it may be instructive to compare the asymptotic values to the exact values obtained earlier on this page.
70. Recovering the sum of all coefficients
Given a generating function for a convergent series ∑i aizi, we can compute the sum of all the ai by setting z to 1. Unfortunately, for many common generating functions setting z=1 yields 0/0 (if it yields something else divided by zero then the series diverges). In this case we can recover the correct sum by taking the limit as z goes to 1 using L'Hôpital's_rule, which says that limx→c f(x)/g(x) = limx→c f'(x)/g'(x) when the latter limit exists and either f(c) = g(c) = 0 or f(c) = g(c) = infinity.7
70.1. Example
Let's derive the formula for 1+2+...+n. We'll start with the generating function for the series ∑i=0n zi, which is (1-z^n+1)/(1-z). Applying the z d/dz method gives us

Plugging z=1 into this expression gives (1-(n+1)+n)/(1-1) = 0/0, which does not make us happy. So we go to the hospital—twice, since one application of L'Hôpital's rule doesn't get rid of our 0/0 problem:

which is our usual formula. Gauss's childhood proof is a lot quicker, but the generating-function proof is something that we could in principle automate most of the work using a computer_algebra_system, and it doesn't require much creativity or intelligence. So it might be the weapon of choice for nastier problems where no clever proof comes to mind.
More examples of this technique can be found on the BinomialCoefficients page, where the binomial theorem applied to (1+x)n (which is really just a generating function for ∑ (n choose i) zi) is used to add up various sums of binomial coefficients.
71. A recursive generating function
Let's suppose we want to count binary trees with n internal nodes. We can obtain such a tree either by (a) choosing an empty tree (g.f.: z0 = 1); or (b) choosing a root with weight 1 (g.f. 1⋅z1 = z, since we can choose it in exactly one way), and two subtrees (g.f. = F2 where F is the g.f. for trees). This gives us a recursive definition
F = 1 + zF2.
Solving for F using the quadratic formula gives
![\[F = \frac{1 \pm \sqrt{1 - 4z}}{2z}.\] \[F = \frac{1 \pm \sqrt{1 - 4z}}{2z}.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_e4502696ef9789c7bc711964d6ec777797547593_p1.png)
That 2z in the denominator may cause us trouble later, but let's worry about that when the time comes. First we need to figure out how to extract coefficients from the square root term.
The binomial theorem says
![\[\sqrt{1-4z} = (1-4z)^{1/2} = \sum_{n=0}^{\infty} {1/2 \choose n} (-4z)^n.\] \[\sqrt{1-4z} = (1-4z)^{1/2} = \sum_{n=0}^{\infty} {1/2 \choose n} (-4z)^n.\]](/pinewiki/GeneratingFunctions?action=AttachFile&do=get&target=latex_bc90a7326129914b75e7fb7be6c84fdc1df1e91a_p1.png)
For n ≥ 1, we can expand out the (1/2 choose n) terms as

For n=0, the switch from the big product of odd terms to (2n-2)! divided by the even terms doesn't work, because (2n-2)! is undefined. So here we just use the special case (1/2 choose 0) = 1.
Now plug this nasty expression back into F to get

Here we choose minus for the plus-or-minus to get the right answer and then do a little bit of tidying up of the binomial coefficient.
We can check the first few values of f(n):
n |
f(n) |
0 |
(0 choose 0) = 1 |
1 |
(1/2)(2 choose 1) = 1 |
2 |
(1/3)(4 choose 2) = 6/3 = 2 |
3 |
(1/4)(6 choose 3) = 20/4 = 5 |
and these are consistent with what we get if we draw all the small binary trees by hand.
The numbers (1/(n+1))(2n choose n) show up in a lot of places in combinatorics, and are known as the Catalan_numbers.
72. Summary of operations on generating functions
The following table describes all the nasty things we can do to a generating function. Throughout, we assume F = ∑ fkzk, G = ∑ gkzk, etc.
Operation |
Effect on generating functions |
Effect on coefficients |
Combinatorial interpretation |
Coefficient extraction |
fk = (1/k!) dk/dzk F(z) |z=0 |
|
Find the number of weight k objects. Easy case: f0 = F(0). |
Sum of all coefficients |
F(1) |
Computes ∑ fk |
Count the total number of objects, ignoring weights. |
Shift right |
G = zF |
gk = fk-1 |
Add 1 to the weight of all objects. |
Shift left |
G = z-1(F-F(0)) |
gk = fk+1 |
Subtract 1 from the weight of all objects. |
Pointing |
G = z d/dz F |
gk = k fk |
A G-thing is an F-thing plus a label pointing to one of its units. |
Sum |
H = F+G |
hk=fk+gk |
Every H-thing is either an F-thing or a G-thing (think union) |
Product |
H=FG |
hk = ∑i figk-i |
Every H-thing consists of an F-thing a G-thing (think cartesian product), with the weight of the H-thing equal to the sum of the weights of the F and G things. |
Composition |
H=F∘G |
H = ∑ fkGk |
To make an H-thing, first choose an F-thing of weight m, then bolt onto it m G-things. The weight of the H-thing is the sum of the weights of the G-things. |
Repetition |
G=1/(1-F) |
G = ∑ Fk |
A G-thing is a sequence of zero or more F-things. Note: this is just a special case of composition. |
73. Variants
The exponential generating function or egf for a sequence a0, ... is given by F(z) = ∑ anzn/n!. For example, the egf for the sequence 1, 1, 1, ... is ez = ∑ z^n/n!. Exponential generating functions admit a slightly different set of operations from ordinary generating functions: differentation gives left shift (since the factorials compensate for the exponents coming down), multiplying by z gives bn = nan+1, etc. The main application is that the product F(z)G(z) of two egf's gives the sequence whose n-th term is ∑ (n choose k) akbn-k; so for problems where we want that binomial coefficient in the convolution (e.g. when we are building weight n objects not only by choosing a weight-k object plus a weight-(n-k) object but also by arbitrarily rearranging their unit-weight pieces) we want to use an egf rather than an ogf. We won't use these in CS202, but it's worth knowing they exist.
A probability generating function or pgf is essentially an ordinary generating function where each coefficient an is the probability that some random variable equals n. See RandomVariables for more details.
74. Further reading
RosenBook discusses some basic facts about generating functions in §7.4. ConcreteMathematics gives a more thorough introduction. Herbert Wilf's book generatingfunctionology, which can be downloaded from the web, will tell you more about the subject than you probably want to know.
See http://www.swarthmore.edu/NatSci/echeeve1/Ref/LPSA/PartialFraction/PartialFraction.html for very detailed notes on partial fraction expansion.
75. ProbabilityTheory
Contents
76. History and interpretation
- Gambling: I throw two six-sided dice, what are my chances of seeing a 7?
- Insurance: I insure a typical resident of Smurfington-Upon-Tyne against premature baldness. How likely is it that I have to pay a claim?
Answers to these questions are summarized by a probability, a number in the range 0 to 1 that represents the likelihood that some event occurs. There are two dominant interpretations of this likelihood:
- Frequentist interpretation
- If an event occurs with probability p, then in the limit as I accumulate many examples of similar events, I will see the number of occurrences divided by the number of samples converging to p. For example, if I flip a fair coin over and over again many times, I expect that heads will come up roughly half of the times I flip it, because the probability of coming up heads is 1/2.
- Bayesian interpretation
- When I say that an event occurs with probability p, that means my subjective beliefs about the event would lead me to take a bet that would be profitable on average if this were the real probability. So a Bayesian would take a double-or-nothing bet on a coin coming up heads if they believed that the probability it came up heads was at least 1/2.
Frequentists and Bayesians have historically spent a lot of time arguing with each other over which interpretation makes sense. The usual argument against frequentist probability is that it only works for repeatable experiments, and doesn't allow for statements like "the probability that it will rain tomorrow is 50%" or the even more problematic "based on what I know, there is a 50% probability that it rained yesterday". The usual argument against Bayesian probability is that it's hopelessly subjective—it's possible (even likely) that my subjective guesses about the probability that it will rain tomorrow are not the same as yours. As mathematicians, we can ignore such arguments, and treat probability axiomatically as just another form of counting, where we normalize everything so that we always end up counting to exactly 1.
(Note: This caricature of the debate over interpreting probability is thoroughly incomplete. For a thoroughly complete discussion, see Probability, Interpretations Of at the Stanford Encyclopedia of Philosophy.)
77. Probability axioms
Coming up with axioms for probabilities that work in all the cases we want to consider took much longer than anybody expected, and the current set in common use only go back to the 1930's. Before presenting these, let's talk a bit about the basic ideas of probability.
An event A is something that might happen, or might not; it acts like a predicate over possible outcomes. The probability Pr[A] of an event A is a real number in the range 0 to 1, that must satisfy certain consistency rules like Pr[¬A] = 1-Pr[A].
In discrete probability, there is a finite set of atoms, each with an assigned probability, and every event is a union of atoms. The probability assigned to an event is the sum of the probabilities assigned to the atoms it contains. For example, we could consider rolling two six-sided dice. The atoms are the pairs (i,j) that give the value on the first and second die, and we assign a probability of 1/36 to each pair. The probability that we roll a 7 is the sum of the cases (1,6), (2,5), (3,4), (4,3), (5,2), and (6,1), or 6/36 = 1/6.
Discrete probability doesn't work if we have infinitely many atoms. Suppose we roll a pair of dice infinitely many times (e.g., because we want to know the probability that we never accumulate more 6's than 7's in this infinite sequence). Now there are infinitely many possible outcomes: all the sequences of pairs (i,j). If we make all these outcomes equally likely, we have to assign each a probability of zero. But then how do we get back to a probability of 1/6 that the first roll comes up 7?
77.1. The Kolmogorov axioms
A triple (S,F,P) is a probability space if S is a set of outcomes (where each outcome specifies everything that ever happens, in complete detail); F is a sigma-algebra, which is a family of subsets of S, called measurable sets, that is closed under complement (i.e., if A is in F then S-A is in F) and countable union (union of A1, A2, ... is in F if each set is); and P is a probability measure that assigns a number in [0,1] to each set in F. The measure P must satisfy three axioms:
- P(S) = 1.
- P(Ø) = 0.
For any sequence of pairwise disjoint events A1, A2, A3, ..., P(∪Ai) = ∑P(Ai).
From these one can derive rules like P(S-A) = 1-P(A) etc.
Most of the time, S is finite, and we can just make F include all subsets of S, and define Pr[A] to be the sum of Pr[{x}] over all x in A; this gets us back to the discrete probability model we had before.
77.2. Examples of probability spaces
- S = {H,T}, F = ℘S, Pr[A] = |A|/2. This represents a fair coin with two outcomes H and T that each occur with probability 1/2.
- S = {H,T}, F = ℘S, Pr[{H}] = p, Pr[{T}] = 1-p. This represents a biased coin, where H comes up with probability p.
- S = { (i,j): i,j∈{1,2,3,4,5,6} }, F = ℘S, Pr[A] = |A|/36. Roll of two fair dice. A typical event might be "the total roll is 4", which is the set { (1,3), (2,2), (3,1) } with probability 3/36 = 1/12.
S = ℕ, F = ℘S, Pr[A] = ∑n∈A 2-n-1. This is an infinite probability space; a real-world process that might generate it is to flip a fair coin repeatedly and count how many times it comes up tails before the first time it comes up heads. Note that even though it is infinite, we can still define all probabilities by summing over atoms: Pr[0] = 1/2, Pr[1] = 1/4, Pr[2] = 1/8, etc.
It's unusual for anybody doing probability to actually write out the details of the probability space like this. Much more often, a writer will just assert the probabilities of a few basic events (e.g. Pr[H] = 1/2), and claim that any other probability that can be deduced from these initial probabilities from the axioms also holds (e.g. Pr[T] = 1-Pr[H] = 1/2). The main reason Kolmogorov gets his name attached to the axioms is that he was responsible for Kolmogorov's existence theorem, which says (speaking very informally) that as long as your initial assertions are consistent, there exists a probability space that makes them and all their consequences true.
78. Probability as counting
The easiest probability space to work with is a uniform discrete probability space, which has N outcomes each of which occurs with probability 1/N. If someone announces that some quantity is "random" without specifying probabilities (especially if that someone is a computer scientist), the odds are that what they mean is that each possible value of the quantity is equally likely. If that someone is being more careful, they would say that the quantity is "drawn uniformly at random" from a particular set.
Such spaces are among the oldest studied in probability, and go back to the very early days of probability theory where randomness was almost always expressed in terms of pulling tokens out of well-mixed urns, because such urn models where one of the few situtations where everybody agreed on what the probabilities should be.
78.1. Examples
A random bit has two outcomes, 0 and 1, and each occurs with probability 1/2.
A die roll has six outcomes, 1 through 6, and each occurs with probability 1/6.
- A roll of two dice has 36 outcomes (order of the dice matters); each occurs with probability 1/36.
A random n-bit string of length n has 2n outcomes; each occurs with probability 2-n. The probability that exactly 1 bit is a 1 is obtained by counting all strings with a single 1 and dividing by 2n: n2-n.
A poker hand consists of a subset of 5 cards drawn uniformly at random from a deck of 52 cards. Depending on whether the order of the 5 cards is considered important (usually it isn't), there are either
 or (52)5 possible hands. The probability of getting a flush (all 5 cards in the hand drawn from the same suit of 13 cards) is
or (52)5 possible hands. The probability of getting a flush (all 5 cards in the hand drawn from the same suit of 13 cards) is  ; there are 4 choices of suits, and
; there are 4 choices of suits, and  ways to draw 5 cards from each suit.
ways to draw 5 cards from each suit. A random permutation on n items has n! outcomes, one for each possible permutation. A typical event might be that the first element of a random permutation of 1..n is 1; this occurs with probability (n-1)!/n! = 1/n. Another example of a random permutation might be a uniform shuffling of a 52-card deck (difficult to achieve in practice!): here the probability that we get a particular set of 5 cards as the first 5 in the deck is obtained by counting all the permutations that have those 5 cards in the first 5 positions (there are 5!×47! of them) divided by 52!. The result is the same
 that we get from the uniform poker hands.
that we get from the uniform poker hands.
79. Independence and the intersection of two events
Events A and B are independent if Pr[A∩B] = Pr[A]·Pr[B]. In general, a group of events {Ai} is independent if each Ai is independent of any event defined only in terms of the other events.
It can be dangerous to assume that events are independent when they aren't, but quite often when describing a probability space we will explicitly state that certain events are independent. For example, one typically describes the space of random n-bit strings (or n coin flips) by saying that one has n independent random bits and then deriving that each particular sequence occurs with probability 2-n rather than starting with each sequence occuring with probability 2-n and then calculating that each particular bit is 1 with independent probability 1/2; the first description makes much more of the structure of the probability space explicitly, and so is more directly useful in calculation.
79.1. Examples
What is the probability of getting two heads on independent coin flips? Pr[H1∩H2] = (1/2)(1/2) = 1/4.
Suppose the coin-flips are not independent (maybe the two coins are glued together). What is the probability of getting two heads? This can range anywhere from zero (coin 2 always comes up the opposite of coin 1) to 1/2 (if coin 1 comes up heads, so does coin 2).
What is the probability that both you and I draw a flush (all 5 cards the same suit) from the same poker deck? Since we are fighting over the same collection of same-suit subsets, we'd expect Pr[A∩B] < Pr[A] Pr[B]—the event that you get a flush (A) is not independent of the event that I get a flush (B), and we'd have to calculate the probability of both by counting all ways to draw two hands that are both flushes. But if we put your cards back and then shuffle the deck again, the events in this new case are independent, and we can just square the Pr[flush] we calculated before.
Suppose the Red Sox play the Yankees. What is the probability that the final score is exactly 4-4? Amazingly, it appears that it is equal to Pr[Red Sox score 4 runs against the Yankees]*Pr[Yankees score 4 runs against the Red Sox] (see http://arXiv.org/abs/math/0509698 for a paper discussing this issue)—to the extent we can measure the underlying probability distribution, the score of each team in a professional baseball game appears to be independent of the score of the other team.
80. Union of two events
What is the probability of A∪B? If A and B are disjoint, then the axioms give Pr[A∪B] = Pr[A] + Pr[B]. But what if A and B are not disjoint?
By analogy to inclusion-exclusion in counting we would expect that
- Pr[A∪B] = Pr[A] + Pr[B] - Pr[A∩B].
Intuitively, when we sum the probabilities of A and B we double-count the event that both occur, and must subtract it off to compensate. To prove this formally, consider the events A∩B, A∩¬B, and ¬A∩B. These are disjoint, so the probability of the union of any subset of this set of events is equal to the sum of its components. So in particular we have
- Pr[A] + Pr[B] - Pr[A∩B] = (Pr[A∩B] + Pr[A∩¬B]) + (Pr[A∩B] + Pr[¬A∩B]) - Pr[A∩B] = Pr[A∩B] + Pr[A∩¬B] + Pr[¬A∩B] = Pr[A∪B].
80.1. Examples
What is the probability of getting at least one head out of two independent coin-flips? Pr[H1∩H2] = 1/2 + 1/2 - (1/2)(1/2) = 3/4.
What is the probability of getting at least one head out of two coin-flips, when the coin-flips are not independent? Here again we can get any probability from 0 to 1, depending on what 1-Pr[H1H2] is.
81. Conditional probability
Suppose I want to answer the question "What is the probability that my dice add up to 6 if I know that the first one is an odd number?" This question involves conditional probability, where we calculate a probability subject to some conditions. The probability of an event A conditioned on an event B, written Pr(A|B), is defined by the formula
![\[\Pr[A|B] = \frac{\Pr[A \cap B]}{\Pr[B]}.\] \[\Pr[A|B] = \frac{\Pr[A \cap B]}{\Pr[B]}.\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_71387d88b914d57018d52d8c60e4c8024ded5150_p1.png)
One way to think about this is that when we assert that B occurs we are in effect replacing the entire probability space with just the part that sits in B. So we have to divide all of our probabilities by Pr[B] in order to make Pr[B|B] = 1, and we have to replace A with A∩B to exclude the part of A that can't happen any more.
Note also that conditioning on B only makes sense if Pr[B] > 0. If Pr[B] = 0, Pr[A|B] is undefined.
81.1. Conditional probabilities and intersections of non-independent events
Simple algebraic manipulation gives
![\[\Pr[A\cap B] = \Pr[A|B] \Pr[B].\] \[\Pr[A\cap B] = \Pr[A|B] \Pr[B].\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_0419efeae636400dadbcb3cfc4a9560f48cc5b18_p1.png)
So one of the ways to compute the probability of two events occurring is to compute the probability of one of them, and the multiply by the probability that the second occurs conditioned on the first. For example, if my attempt to reach the summit of Mount Everest requires that I first learn how to climb mountains (Pr[B] = 10%) and then make it to the top safely (Pr[A|B] = 90%), then my chances of getting to the top are Pr[A∩B] = (90%)(10%) = 9%.
We can do this for sequences of events as well. Suppose that I have an urn that starts with k black balls and 1 red ball. In each of n trials I draw one ball uniformly at random from the urn. If it is red, I give up. If it is black, I put the ball back and add another black ball, thus increasing the number of balls by 1. What is the probability that on every trial I get a black ball?
Let Ai be the event that I get a black ball on the first i trials. Then Pr[A0] = 1, and for larger i we have Pr[Ai] = Pr[Ai|Ai-1] Pr[Ai-1]. If Ai-1 holds, then at the time of the i-th trial we have k+i total balls in the urn of which one is red. So the probability that we draw a black ball is 1-1/(k+i) = (k+i-1)/(k+i). By induction we can then show that
![\[
\Pr[A_i] = \prod_{j=1}^{i} \frac{k+j-1}{k+j}.
\] \[
\Pr[A_i] = \prod_{j=1}^{i} \frac{k+j-1}{k+j}.
\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_04afa816e5b2ef1de11c208cc0df65045d626e07_p1.png)
This is an example of a collapsing product, where the denominator of each fraction cancels out the numerator of the next; we are left only with the denominator k+i of the last term and the numerator k of the first, giving Pr[Ai] = k/(k+i). It follows that we make it through all n trials with probability Pr[An] = k/(k+n).
81.2. The law of total probability
We can use the fact that A is the disjoint union of A∧B and A∧¬B to get Pr[A] by case analysis:
![\[\Pr[A] = \Pr[A\cap B] + \Pr[A \cap \overline{B}] = \Pr[A|B]\Pr[B] + \Pr[A|\overline{B}]\Pr[\overline{B}].\] \[\Pr[A] = \Pr[A\cap B] + \Pr[A \cap \overline{B}] = \Pr[A|B]\Pr[B] + \Pr[A|\overline{B}]\Pr[\overline{B}].\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_059de701c3da4c38dc139186a5a91a327dcaf8f1_p1.png)
So, for example, there is a 20% chance I can make it to the top of Mt Everest safely without learning how to climb first, my chances of getting there go up to (90%)(10%) + (20%)(90%) = 27%.
This method is sometimes given the rather grandiose name of the law of total probability. The most general version is that if B1..Bn are all disjoint events, then
![\[
\Pr[A] = \sum_{i=1}^{n} \Pr[A|B_i] \Pr[B_i]
\] \[
\Pr[A] = \sum_{i=1}^{n} \Pr[A|B_i] \Pr[B_i]
\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_a82538ebbd2f11978637bc0635630a722d46ace8_p1.png)
81.3. Bayes's formula
If one knows Pr[A|B], Pr[A|¬B], and Pr[B], it's possible to compute Pr[B|A]:
![\[\Pr[B|A] = \frac{\Pr[A\cap B]}{\Pr[A]} = \frac{\Pr[A|B] \Pr[B]}{\Pr[A]}
= \frac{\Pr[A|B] \Pr[B]}{\Pr[A|B]\Pr[B] + \Pr[A|\overline{B}]\Pr[\overline{B}]}.\] \[\Pr[B|A] = \frac{\Pr[A\cap B]}{\Pr[A]} = \frac{\Pr[A|B] \Pr[B]}{\Pr[A]}
= \frac{\Pr[A|B] \Pr[B]}{\Pr[A|B]\Pr[B] + \Pr[A|\overline{B}]\Pr[\overline{B}]}.\]](/pinewiki/ProbabilityTheory?action=AttachFile&do=get&target=latex_35a4abc3661a3fc05fb397b3d236f287466ddc49_p1.png)
This formula is used heavily in statistics, where it goes by the name of Bayes's formula. Say that you have an Airport Terrorist Detector that lights up 75% of the time when inserted into the nostrils of a Terrorist, but lights up 0.1% of the time when inserted into the nostrils of a non-Terrorist. Suppose that for other reasons you know that Granny has only a 0.01% chance of being a Terrorist. What is the probability that Granny is a Terrorist if the detector lights up?
Let B be the event "Granny is a terrorist" and A the event "Detector lights up". Then Pr[B|A] = (75% * 0.01%)/(75% * 0.01% + 0.1% * 99.99%) ≅ 0.07495%. This examples show how even a small "false negative" rate can make it difficult to interpret the results of tests for rare conditions.
82. Random variables
A random variable X is a function from a probability space to some codomain; for more details see RandomVariables.
83. RandomVariables
Contents
84. Random variables
A random variable X is a variable that takes on particular values randomly. This means that for each possible value x, there is an event [X=x] with some probability of occurring that corresponds to X (the random variable, usually written as an upper-case letter) taking on the value x (some fixed value).
Examples of random variables:
Indicator variables: The indicator variable for an event A is a variable X that is 1 if A occurs and 0 if it doesn't (i.e., X(ω) = 1 if ω∈A and 0 otherwise). Indicator variables are often written using the Greek letter chi (e.g. χA) or using bracket notation (e.g., [A], [Y2 > 3], [all six coins come up heads]).
- Functions of random variables: Any function you are likely to run across of a random variable or random variables is a random variable, e.g. X+Y, XY, log X, etc.
- Counts: Flip a fair coin n times and let X be the number of times it comes up heads. Then X is an integer-valued random variable.
Random sets and structures: Suppose that we have a set T of n elements, and we pick out a subset U by flipping an independent fair coin for each element to decide whether to include it. Then U is a set-valued random variable. Or we could consider the infinite sequence X0, X1, X2, ..., where X0 = 0 and Xn+1 is either Xn+1 or Xn-1, which being chosen by an independent fair coin flip. Then we can think of the entire sequence X as a sequence-valued random variable.
85. The distribution of a random variable
The distribution of a random variable describes the probability that it takes on various values. For discrete random variables (variables that take on only countably many values, each with nonzero probability), the distribution is most easily described by just giving the probability Pr[X=x] for each value x.8
Often if we know the distribution of a random variable, we don't bother worrying about what the underlying probability space is. The reason for this is we can just take Ω to be the range of the random variable, and define Pr[ω] for each ω∈Ω to be Pr[X=ω]. For example, a six-sided die corresponds to taking Ω = {1,2,3,4,5,6}, assigning Pr[ω] = 1/6 for all ω∈Ω, and letting X(ω) = ω.
The same thing works if we have multiple random variables, but now we let each point in the space be a tuple that gives the values of all of the variables. Specifying the probability in this case is done using a joint distribution (see below).
85.1. Some standard distributions
Here are some common distributions for a random variable X:
- Bernoulli distribution
- Pr[X = 1] = p, Pr[X = 0] = q, where p is a parameter of the distribution and q = 1-p. This corresponds to a single biased coin-flip.
- Binomial distribution
Pr[X = k] = (n choose k) pk q(n-k), where n and p are parameters of the distribution and q = 1-p. This corresponds to the sum of n biased coin-flips.
- Geometric distribution
Pr[X = k] = qkp, where p is a parameter of the distribution and q is again equal to 1-p. This corresponds to number of tails we flip before we get the first head in a sequence of biased coin-flips.
- Poisson distribution
Pr[X = k] = e-λλk/k!. This is what happens to a binomial distribution when we fix p = λ/n and then take the limit as n goes to infinity; we can think of it as counting the number of events that occur in one time unit if the events occur at a constant continuous rate that averages λ events per time unit. The canonical example is radioactive decay.
- Uniform distribution
- The distribution function F of X is given by F(x) = 0 when x ≤ a, (x-a)/(b-a) when a ≤ x ≤ b, and 1 when b ≤ x, where a and b are parameters of the distribution. This is a continuous random variable that has equal probability of landing anywhere in the [a,b] interval.
Another very important distribution is the normal distribution, but it's not discrete so we would need more machinery to talk about it.
85.2. Joint distributions
Two or more random variables can be described using a joint distribution. For discrete random variables, this just gives Pr[X=x ∧ Y=y] for all fixed values x and y, or in general gives Pr[∀i Xi=xi].
Given a joint distribution on X and Y, we can recover the distribution on X or Y individually by summing up cases: Pr[X=x] = ∑y Pr[X=x ∧ Y=y]. The distribution of X obtained in this way is called a marginal distribution of the original joint distribution. In general we can't go in the other direction, because just knowing the marginal distributions doesn't tell us how the random variables might be related to each other.
Examples:
- Let X and Y be six-sided dice. Then Pr[X=x ∧ Y=y] = 1/36 for all values of x and y in the right range. The underlying probability space consists of all pairs (x,y) in {1,2,3,4,6}×{1,2,3,4,5,6}.
- Let X be a six-sided die and let Y = 7 - X. Then Pr[X=x ∧ Y=y] = 1/6 if 1 ≤ x ≤ 6 and y = 7-x, and 0 otherwise, with the underlying probability space most easily described by including just six points for the X values (although we could also do {1,2,3,4,5,6}×{1,2,3,4,5,6} as in the previous case, just assigning probability 0 to most of the points). However, even though the joint distribution is very different from the previous case, the marginal distributions of X and Y are exactly the same as before: each of X and Y takes on all values in {1,2,3,4,5,6} with equal probability.
85.3. Independence of random variables
The difference between the two preceding examples is that in the first case, X and Y are independent, and in the second case, they aren't.
Two random variables X and Y are independent if any pair of events of the form X∈A, Y∈B are independent. For discrete random variables, it is enough to show that Pr[X=x ∧ Y=y] = Pr[X=x]⋅Pr[Y=y], or in other words that the events [X=x] and [Y=y] are independent for all values x and y. In practice, we will typically either be told that two random variables are independent or deduce it from how they are generated.
Examples:
Roll two six-sided dice, and let X and Y be the values of the dice. By convention we assume that these values are independent. This means for example that Pr[X∈{1,2,3} ∧ Y∈{1,2,3}] = [Pr[X∈{1,2,3}]⋅Pr[Y∈{1,2,3}] = (1/2)(1/2) = 1/4, which is a slightly easier computation than counting up the 9 cases (and then argue that each occurs with probability (1/6)2, which requires knowing that X and Y are independent).
- Take the same X and Y, and let Z = X+Y. Now Z and X are not independent, because Pr[X=1 ∧ Z=12] = 0, which is not equal to Pr[X=1]⋅Pr[Z=12] = (1/6)(1/36) = 1/216.
- Place two radioactive sources on opposite sides of the Earth, and let X and Y be the number of radioactive decay events in each source during some 10ms interval. Since the sources are 42ms away from each other at the speed of light, we can assert that either X and Y are independent, or the world doesn't behave the way the physicists think it does. This is an example of variables being independent because they are physically independent.
- Roll one six-sided die X, and let Y = ⌈X/2⌉ and Z = X mod 2. Then Y and Z are independent, even though they are generated using the same physical process.
In general, if we have a collection of random variables Xi, we say that they are all independent if the joint distribution is the product of the marginal distributions, i.e. if Pr[∀i Xi=xi] = ∏i Pr[Xi=xi]. It may be that a collection of random variables is not independent even though all subcollections are.
- Let X and Y be fair coin-flips, and let Z = X⊕Y. Then any two of X, Y, and Z are independent, but the three variables X, Y, and Z are not independent, because (for example) Pr[X = 0 ∧ Y = 0 ∧ Z = 0] = 1/4 instead of 1/8 as one would get by taking the product of the marginal distributions.
Since we can compute the joint distribution from the marginal distributions for independent variables, we will often just specify the marginal distributions and declare that a collection of random variables are independent. This implicitly gives us an underlying probability space consisting of all sequences of values for the variables.
86. The expectation of a random variable
For a real-valued random variable X, its expectation E[X] (sometimes just EX) is its average value, weighted by probability.9> For discrete random variables, the expectation is defined by
![\[\E[X] = \sum_{x} x \Pr[X=x].\] \[\E[X] = \sum_{x} x \Pr[X=x].\]](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_948ac738e65193d25c6990ef42b4baf7ae6abc9e_p1.png)
- Example (discrete variable)
- Let X be the number rolled with a fair six-sided die. Then E[X] = (1/6) (1+2+3+4+5+6) = 3½.
- Example (unbounded discrete variable)
Let X be a geometric random variable with parameter p, i.e., let Pr[X = k] = qkp, where q = 1-p. Then E[X] =
 .
.
Expectation is a way to summarize the distribution of a random variable without giving all the details. If you take the average of many independent copies of a random variable, you will be likely to get a value close to the expectation. Expectations are also used in decision theory to compare different choices. For example, given a choice between a 50% chance of winning $100 (expected value: $50) and a 20% chance of winning $1000 (expected value: $200), a rational decision maker would take the second option. Whether ordinary human beings correspond to an economist's notion of a rational decision maker often depends on other details of the situation.
Terminology note: If you hear somebody say that some random variable X takes on the value z on average, this usually means that E[X] = z.
86.1. Variables without expectations
If a random variable has a particularly annoying distribution, it may not have a finite expectation, even thought the variable itself takes on only finite values. This happens if the sum for the expectation diverges.
For example, suppose I start with a dollar, and double my money every time a fair coin-flip comes up heads. If the coin comes up tails, I keep whatever I have at that point. What is my expected wealth at the end of this process?
Let X be the number of times I get heads. Then X is just a geometric random variable with p = 1/2, so Pr[X=k] = (1-(1/2))k(1/2)k = 2-k-1. My wealth is also a random variable: 2X. If we try to compute E[2X], we get
![\begin{align*}
\E[2^X]
&= \sum_{k=0}^{\infty} 2^k \Pr[X = k]
\\
&= \sum_{k=0}^{\infty} 2^k \cdot 2^{-k-1}
\\
&= \sum_{k=0}^{\infty} \frac{1}{2},
\end{align*} \begin{align*}
\E[2^X]
&= \sum_{k=0}^{\infty} 2^k \Pr[X = k]
\\
&= \sum_{k=0}^{\infty} 2^k \cdot 2^{-k-1}
\\
&= \sum_{k=0}^{\infty} \frac{1}{2},
\end{align*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_3cdcbbbc4cd83bf1d21a703b8b8c6646e10223ae_p1.png)
which diverges. Typically we say that a random variable like this has no expected value, although sometimes you will see people writing E[2X] = ∞.
(For an even nastier case, consider what happens with E[(-2)X].)
86.2. Expectation of a sum
The expectation operator is linear: this means that E(X+Y) = E(X)+E(Y) and E(aX) = aE(X) when a is a constant. This fact holds for all random variables X and Y, whether they are independent or not, and is not hard to prove for discrete probability spaces:
![\begin{align*}
\E[aX+Y]
&= \sum_{x,y} (ax+y) \Pr[X = x \wedge Y = x]
\\
&=
a \sum_{x,y} x \Pr[X = x \wedge Y = x]
+ \sum_{x,y} y \Pr[X = x \wedge Y = x]
\\
&=
a \sum_x x \sum_y \Pr[X = x \wedge Y = x]
+ \sum_y y \sum_x \Pr[X = x \wedge Y = x]
\\
&=
a \sum_x x \Pr[X=x]
+ \sum_y y \Pr[Y=y]
\\
&=
a\E[X]+\E[Y].
\end{align*} \begin{align*}
\E[aX+Y]
&= \sum_{x,y} (ax+y) \Pr[X = x \wedge Y = x]
\\
&=
a \sum_{x,y} x \Pr[X = x \wedge Y = x]
+ \sum_{x,y} y \Pr[X = x \wedge Y = x]
\\
&=
a \sum_x x \sum_y \Pr[X = x \wedge Y = x]
+ \sum_y y \sum_x \Pr[X = x \wedge Y = x]
\\
&=
a \sum_x x \Pr[X=x]
+ \sum_y y \Pr[Y=y]
\\
&=
a\E[X]+\E[Y].
\end{align*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_55f5298cfc20b5e9f7b0aa92bbcd61b735e09f89_p1.png)
Linearity of expectation makes computing many expectations easy. Example: Flip a fair coin n times, and let X be the number of heads. What is E[X]? We can solve this problem by letting Xi be the indicator variable for the event "coin i came up heads". Then X = ∑i Xi and EX = E[∑i Xi] = ∑i EXi = n(½) = n/2. In principle it is possible to calculate the same value from the distribution of X (which involves a lot of binomial coefficients), but linearity of expectation is much easier.
- Example
- Choose a random permutation f, i.e. a random bijection from 1..n → 1..n. What is the expected number of values i for which f(i) = i?
- Solution
Let Xi be the indicator variable for the event that f(i) = i. Then we are looking for E[X1 + X2 + ... Xn] = E[X1] + E[X2] + ... E[Xn]. But E[Xi] is just 1/n for each i, so the sum is n(1/n) = 1. (Calculating this by computing Pr[∑Xi] = x first would be very painful.)
86.3. Expectation of a product
For products of random variables, the situation is more complicated. Here the rule is that E[XY] = E[X]⋅E[Y] if X and Y are independent. But if X and Y are not independent, their expectation can be arbitrary.
- Example
- Roll 2 dice and take their product. What value do we get on average? The product formula gives E[XY] = E[X]E[Y] = (7/2)² = (49/4) = 12¼. We could also calculate this directly by summing over all 36 cases, but it would take a while.
- Example
- Roll 1 die and multiply it by itself. What value do we get on average? Here we are no longer dealing with independent random variables, so we have to do it the hard way: E[X²] = (1²+2²+3²+4²+5²+6²)/6 = 91/6 = 15⅙. This is substantially higher than when the dice are uncorrelated. (Exercise: How can you rig the second die so it still comes up with each value ⅙ of the time but minimizes E[XY]?)
We can prove the product rule without too much trouble for discrete random variables. The easiest way is to start from the right-hand side.
![\begin{eqnarray*}
\E[X] \cdot \E[Y]
&=&
\left(\sum_{x} x \Pr[X=x]\right)\left(\sum_{y} y \Pr[Y=y]\right)
\\
&=&
\sum_{x,y} xy \Pr[X=x] \Pr[Y=y]
\\
&=&
\sum_{z} z \left(\sum_{x,y, xy=z} \Pr[X=x] \Pr[Y=y]\right)
\\
&=&
\sum_{z} z \left(\sum_{x,y, xy=z} \Pr[X=x \wedge Y=y]\right)
\\
&=&
\sum_{z} z \Pr[XY=z]
\\
&=&
\E[XY].
\end{eqnarray*} \begin{eqnarray*}
\E[X] \cdot \E[Y]
&=&
\left(\sum_{x} x \Pr[X=x]\right)\left(\sum_{y} y \Pr[Y=y]\right)
\\
&=&
\sum_{x,y} xy \Pr[X=x] \Pr[Y=y]
\\
&=&
\sum_{z} z \left(\sum_{x,y, xy=z} \Pr[X=x] \Pr[Y=y]\right)
\\
&=&
\sum_{z} z \left(\sum_{x,y, xy=z} \Pr[X=x \wedge Y=y]\right)
\\
&=&
\sum_{z} z \Pr[XY=z]
\\
&=&
\E[XY].
\end{eqnarray*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_f931f8689bd0ebd694669271b62c7ab2847a39b8_p1.png)
Here we use independence in going from Pr[X=x] Pr[Y=y] to Pr[X=x ∧ Y=y] and use the union rule to convert the x,y sum into Pr[XY=z].
86.4. Conditional expectation
Like conditional probability, there is also a notion of conditional expectation. The simplest version of conditional expectation conditions on a single event A, is written E[X|A], and is defined for discrete random variables by
![\[E[X|A] = \sum_{x} x \Pr[X=x|A].\] \[E[X|A] = \sum_{x} x \Pr[X=x|A].\]](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_c2a90303551ca97f7a8915691557b1e7ef6c1101_p1.png)
This is exactly the same as unconditioned expectation except that the probabilities are now conditioned on A.
- Example
- What is the expected value of a six-sided die conditioned on not rolling a 1? The conditional probability of getting 1 is now 0, and the conditional probability of each of the remaining 5 values is 1/5, so we get (1/5)(2+3+4+5+6) = 4.
Conditional expectation acts very much like regular expectation, so for example we have E[aX+bY|A] = aE[X|A] + bE[Y|A].
One of the most useful applications of conditional expectation is that it allows computing (unconditional) expectations by case analysis, using the fact that
- E[X] = E[X|A]Pr[A] + E[X|¬A]Pr[¬A].
86.4.1. Examples
86.4.1.1. The Treasure on Mt Everest
I have a 50% chance of reaching the top of Mt Everest, where Sir Edmund Hilary and Tenzing Norgay hid somewhere between 0 and 10 kilograms of gold (a random variable with uniform distribution). How much gold do I expect to bring home? Compute E[X] = E[X|reached the top]Pr[reached the top] + E[X|didn't make it]Pr[didn't make it] = 5⋅0.5 + 0⋅0.5 = 2.5.
86.4.1.2. Waiting times
Suppose I flip a coin that comes up heads with probability p until I get heads. How many times on average do I flip the coin?
We'll let X be the number of coin flips. Conditioning on whether the coin comes up heads on the first flip gives E[X] = 1⋅p + (1+E[X'])⋅(1-p), where X' is random variable counting the number of coin-flips needed to get heads ignoring the first coin-flip. But since X' has the same distribution as X, we get EX = p + (1-p) (1+EX) or EX = (p+(1-p))/p = 1/p. So a fair coin must be flipped twice on average to get a head, which is about what we'd expect if we hadn't thought about it much.
86.4.1.3. Rewarding success and punishing failure
Suppose I have my experimental test subjects complete a task that gets scored on a scale of 0 to 100. I decide to test whether rewarding success is a better strategy for improving outcomes than punishing failure. So for any subject that scores high than 50, I give them a chocolate bar. For any subject that scores lower than 50, I give them an electric shock. (Students who score exactly 50 get nothing.) I then have them each perform the task a second time and measure the average change in their scores. What happens?
Let's suppose that there is no effect whatsoever of my rewards and punishments, and that each test subject obtains each possible score with equal probability 1/101. Now let's calculate the average improvement for test subjects who initially score less than 50 or greater than 50. Call the outcome on the first test X and the outcome on the second test Y.
In the first case, we are computing E[Y-X | X < 50]. This is the same as E[Y | X < 50] - E[X | X<50] = E[Y] - E[X|X<50] = 50 - 24.5 = +25.5. So punishing failure produces a 25.5 point improvement on average.
In the second case, we are computing E[Y-X | X > 50]. This is the same as E[Y | X > 50] - E[X | X>50] = E[Y] - E[X|X>50] = 50 - 75.5 = -25.5. So rewarding success produces a 25.5 point decline on average.
Clearly this suggests that we punish failure if we want improvements and reward success if we want backsliding. This is intuitively correct: punishing failure encourages our slacker test subjects to do better next time, while rewarding success just makes them lazy and complacent. But since the test outcomes don't depend on anything we are doing, we get exactly the same answer if we reward failure and punish success: in the former case, a +25.5 point average change, in the later a -25.5 point average change. This is also intuitively correct: rewarding failure makes our subjects like the test so that they will try to do better next time, while punishing success makes them feel that it isn't worth it. From this we learn that our intuitions10 provide powerful tools for rationalizing almost any outcome in terms of the good or bad behavior of our test subjects. A more careful analysis shows that we performed the wrong comparison, and we are the victim of regression to the mean.
For a real-world example of how similar problems can arise in processing data, the United States Bureau of Labor Statistics defines a small business as any company with 500 or fewer employees. So if a company has 400 employees in 2007, 600 in 2008, and 400 in 2009, then we just saw a net creation of 200 new jobs by a small business in 2007, followed by the destruction of 200 jobs by a large business in 2008. This effect alone accounts for most of the observation that small businesses generate more new jobs than large ones.
86.4.2. Conditioning on a random variable
There is a more general notion of conditional expectation for random variables, where the conditioning is done on some other random variable Y. Unlike E[X|A], which is a constant, the expected value of X conditioned on Y, written E[X|Y], is itself a random variable: when Y = y, it takes on the value E[X|Y=y].
- Example
- Let us compute E[X+Y|X] where X and Y are the values of independent six-sided dice. When X = x, E[X+Y|X] = E[X+Y|X=x] = x+E[Y] = x + 7/2. For the full random variable we can write E[X+Y|X] = X + 7/2.
Another way to get the result in the preceding example is to use some general facts about conditional expectation:
- E[aX+bY|Z] = aE[X|Z] + bE[Y|Z]. This is the conditional-expectation version of linearity of expectation.
- E[X|X] = X. This is immediate from the definition, since E[X|X=x] = x.
- If X and Y are independent, then E[Y|X] = E[Y]. The intuition is that knowing the value of X gives no information about Y, so E[Y|X=x] = E[Y] for any x in the range of X. (To do this formally requires using the fact that Pr[Y=y|X=x] = Pr[Y=y /\ X=x] / Pr[X=x] = Pr[Y=y]Pr[X=x]/Pr[X=x] = Pr[Y=y], provided X and Y are independent.)
- Also useful: E[E[X|Y]] = E[X]. Averaging a second time removes all dependence on Y.
These in principle allow us to do very complicated calculations involving conditional expectation. For example:
- Example
- Let X and Y be the values of independent six-sided dice. What is E[X | X+Y]? Here we observe that X+Y = E[X+Y | X+Y] = E[X | X+Y] + E[Y | X+Y] = 2E[X | X+Y] by symmetry. So E[X | X+Y] = (X+Y)/2. This is pretty much what we'd expect: on average, half the total value is supplied by one of the dice. (It also works well for extreme cases like X+Y = 12 or X+Y = 2, giving a quick check on the formula.)
- Example
What is E[(X+Y)2 | X] when X and Y are independent? Compute E[(X+Y)2 | X] = E[X2 | X] + 2E[XY | X] + E[Y2 | X] = X2 + 2X E[Y] + E[Y2]. For example, if X and Y are independent six-sided dice we have E[(X+Y)2 | X] = X2 + 7X + 91/6, so if you are rolling the dice one at a time and the first one comes up 5, you can expect on average to get a squared total of 25 + 35 + 91/6 = 75 1/6. But if the first one comes up 1, you only get 1 + 7 + 91/6 = 23 1/6 on average.
86.5. Markov's inequality
Knowing the expectation of a random variable gives you some information about it, but different random variables may have the same expectation but very different behavior: consider, for example, the random variable X that is 0 with probability 1/2 and 1 with probability 1/2 and the random variable Y that is 1/2 with probability 1. In some cases we don't care about the average value of a variable so much as its likelihood of reaching some extreme value: for example, if my feet are encased in cement blocks at the beach, knowing that the average high tide is only 1 meter is not as important as knowing whether it ever gets above 2 meters. Markov's inequality lets us bound the probability of unusually high values of non-negative random variables as a function of their expectation. It says that, for any a > 0,
Pr[X > aEX] < 1/a.
This can be proved easily using conditional expectations. We have:
EX = E[X|X > aEX] Pr[X > aEX] + E[X|X ≤ aEX] Pr[X > aEX].
Since X is non-negative, E[X|X ≤ aEX] ≥ 0, so subtracting out the last term on the right-hand side can only make it smaller. This gives:
EX ≥ E[X|X > aEX] Pr[X > aEX] > aEX Pr[X > aEX]
and dividing both side by aEX gives the desired result.
Another version of Markov's inequality replaces > with ≥:
- E[X ≥ aEX] ≤ 1/a.
The proof is essentially the same.
- Example
Suppose that that all you know about high tide is that EX = 1 meter and X ≥ 0. What can we say about the probability that X > 2 meters? Using Markov's inequality, we get Pr[X > 2 meters] = Pr[X > 2EX] < 1/2.
There is, of course, a conditional version of Markov's inequality:
Pr[X > aE[X|A] | A] < 1/a.
This version doesn't get anywhere near as much use as the unconditioned version, but it may be worth remembering that it exists.
87. The variance of a random variable
Expectation tells you the average value of a random variable but it doesn't tell you how far from the average the random variable typically gets: the random variable X = 0 and Y = ±1,000,000,000,000 with equal probability both have expectation 0, though their distributions are very different. Though it is impossible to summarize everything about the spread of a distribution in a single number, a useful approximation for many purposes is the variance Var(X) of a random variable X, which is defined as the expected square of the deviation from the expectation, or E((X-EX)2).
- Example
Let X = 0 or 1 with equal probability. Then EX = 1/2, and (X-EX)2 is always 1/4. So Var(X) = 1/4.
- Example
Let X be the value of a fair six-sided die. Then EX = 7/2, and E((E-EX)2) = (1/6)((1-7/2)2 + (2-7/2)2 + (3-7/2)2 + ... + (6 - 7/2)2) = 35/12.
Computing variance directly from the definition can be tedious. Often it is easier to compute it from E(X2) and EX:
Var[X] = E[(X-EX)2] = E[X2 - 2 X EX + (EX)2] = E[X2] - 2 EX EX + (EX)2 = E[X2] = (EX)2.
(The second-to-last step uses linearity of expectation and the fact that EX is a constant.)
- Example
For X = 0 or 1 with equal probability, we have E[X2] = 1/2 and (EX)2 = 1/4, so Var[X] = 1/4.
- Example
- Let's try the six-sided die again, except this time we'll use an n-sided die. We have
![\begin{eqnarray*}
Var[X] &=& E[X^2] - (E X)^2 \\
&=& \frac{1}{n} \sum_{i=1}^{n} i^2 - \left(\frac{n+1}{2}\right)^2 \\
&=& \frac{1}{n} \cdot \frac{n(n+1)(2n+1)}{6} - \frac{(n+1)^2}{4} \\
&=& \frac{(n+1)(2n+1)}{6} - \frac{(n+1)^2}{4}.
\end{eqnarray*} \begin{eqnarray*}
Var[X] &=& E[X^2] - (E X)^2 \\
&=& \frac{1}{n} \sum_{i=1}^{n} i^2 - \left(\frac{n+1}{2}\right)^2 \\
&=& \frac{1}{n} \cdot \frac{n(n+1)(2n+1)}{6} - \frac{(n+1)^2}{4} \\
&=& \frac{(n+1)(2n+1)}{6} - \frac{(n+1)^2}{4}.
\end{eqnarray*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_61b5eb4c7286194df91afb328fde578258a6123c_p1.png)
When n = 6, this gives 7⋅13/6 - 49/4 = 35/12. (Ok, maybe it isn't always easier).
87.1. Multiplication by constants
Suppose we are asked to compute the variance of aX, where a is a constant. We have
- Var[aX] = E[(aX)²] - E[aX]² = a²E[X²] - (aE[X])² = a² Var[X].
So, for example, if X = 0 or 2 with equal probability, Var[X] = 4⋅(1/4) = 1. This is exactly what we expect given that X-EX is always ±1.
Another consequence is that Var[-X] = (-1)²Var[X] = Var[X]. So variance is not affected by negation.
87.2. The variance of a sum
What is Var[X+Y]? Write
![\begin{eqnarray*}
\mbox{Var}[X+Y]
&=& E[(X+Y)^2] - \left(E[X+Y]\right)^2 \\
&=& E[X^2] + 2E[XY] + E[Y^2] - (EX)^2 - 2 EX \cdot EY - (EY)^2 \\
&=& (E[X^2] - (EX)^2) + (E[Y^2] - (EY)^2) + 2(E[XY] - EX \cdot EY) \\
&=& \mbox{Var}[X] + \mbox{Var}[Y] + 2(E[XY] - EX \cdot EY).
\end{eqnarray*} \begin{eqnarray*}
\mbox{Var}[X+Y]
&=& E[(X+Y)^2] - \left(E[X+Y]\right)^2 \\
&=& E[X^2] + 2E[XY] + E[Y^2] - (EX)^2 - 2 EX \cdot EY - (EY)^2 \\
&=& (E[X^2] - (EX)^2) + (E[Y^2] - (EY)^2) + 2(E[XY] - EX \cdot EY) \\
&=& \mbox{Var}[X] + \mbox{Var}[Y] + 2(E[XY] - EX \cdot EY).
\end{eqnarray*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_282c776f9d20ea4b98d3b4e2b177f8371b48d178_p1.png)
The quantity E[XY] - EX EY is called the covariance of X and Y and is written Cov(X,Y). So we have just shown that
- Var[X+Y] = Var[X] + Var[Y] + 2 Cov(X,Y).
When Cov(X,Y) = 0, or equivalently when E[XY] = EX EY, X and Y are said to be uncorrelated and their variances add. This occurs when X and Y are independent, but may also occur without X and Y being independent.
For larger sums the corresponding formula is
![\[\mbox{Var}\left[\sum_{i=1}^{n} X_i\right] = \sum_{i=1}^{n} \mbox{Var}[X_i] + \sum_{i\neq j} \mbox{Cov}(X,Y).\] \[\mbox{Var}\left[\sum_{i=1}^{n} X_i\right] = \sum_{i=1}^{n} \mbox{Var}[X_i] + \sum_{i\neq j} \mbox{Cov}(X,Y).\]](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_cceee1166d5ef1a6dd59f012d208f23d71ed3f69_p1.png)
This simplifies to Var(∑Xi) = ∑Var(Xi) when the Xi are pairwise independent, so that each pair of distinct Xi and Xj are independent. (This is implied by independence but is not equivalent to it.)
- Example
What is the variance of the number of heads in n independent fair coin-flips? Let Xi be the indicator variable for the event that the i-th flip comes up heads and let X be the sum of the Xi. We have already seen that Var[Xi] = 1/4, so Var[X] = n Var[Xi] = n/4.
- Example
- Let a be a constant. What is the variance of X+a? We have Var[X+a] = Var[X] + Var[a] = Var[X], since (1) E[aX] = aE[X] = E[a]E[X] means that a (considered as a random variable) and X are uncorrelated, and (2) Var[a] = E[a-Ea] = E[a-a] = 0. So shifting a random variable up or down doesn't change its variance.
87.3. Chebyshev's inequality
Variance is an expectation, so we can use Markov's inequality on it. The result is Chebyshev's inequality:
Pr[|X - EX| > r) < Var[X] / r2.
Proof: The event |X - EX| > r is the same as the event (X-EX)2 > r2. By Markov's inequality, the probability that this occurs is at most E[(E-EX)2]/r2 = Var[X]/r2.
87.3.1. Application: showing that a random variable is close to its expectation
This is the usual statistical application.
- Example
Flip a fair coin n times, and let X be the number of heads. What is the probability that |X-n/2| > r? Recall that Var[X] = n/4, so Pr[|X-n/2| > r] < (n/4)/r2 = n/(4r2). So, for example, the chances of deviating from the average by more than 1000 after 1000000 coin-flips is less than 1/4.
- Example
Out of n voters in Saskaloosa County, m plan to vote for Smith for County Dogcatcher. A polling firm samples k voters (with replacement) and asks them who they plan to vote for. Suppose that m < n/2; compute a bound on the probability that the polling firm incorrectly polls a majority for Smith.
Solution: Let Xi be the indicator variable for a Smith vote when the i-th voter is polled and let X = ∑Xi be the total number of pollees who say they will vote for Smith. Let p = EXi = m/n. Then Var[Xi] = p - p2, EX = kp, and Var[X] = k(p-p2). To get a majority in the poll, we need X > k/2 or X-EX > k/2 - kp. Using Chebyshev's inequality, this event occurs with probability at most
![\begin{eqnarray*}
\frac{\mbox{Var}[X]}{(k/2-kp)^2}
&=& \frac{k(p - p^2)}{(k/2-kp)^2} \\
&=& \frac{1}{k} \cdot \frac{p-p^2}{(1/2 - p)^2}.
\end{eqnarray*} \begin{eqnarray*}
\frac{\mbox{Var}[X]}{(k/2-kp)^2}
&=& \frac{k(p - p^2)}{(k/2-kp)^2} \\
&=& \frac{1}{k} \cdot \frac{p-p^2}{(1/2 - p)^2}.
\end{eqnarray*}](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_53ed4f6f801e6bbd9f19d9f0030d0340d088e106_p1.png)
Note that the bound decreases as k grows and (for fixed p) does not depend on n.
In practice, statisticians will use a stronger result called the Central limit theorem, which describes the shape of the distribution of the sum of many independent random variables much more accurately than the bound from Chebyshev's inequality. Designers of randomized algorithms are more likely to use Chernoff bounds.
87.3.2. Application: lower bounds on random variables
Unlike Markov's inequality, which can only show that a random variable can't be too big too often, Chebyshev's inequality can be used to show that a random variable can't be too small, by showing first that its expectation is high and then that its variance is low. For example, suppose that each of the 1030 oxygen molecules in the room is close enough to your mouth to inhale with pairwise independent probability 10-4 (it's a big room). Then the expected number of oxygen molecules near your mouth is a healthy 1030 * 10-4 = 1026. What is the probability that all 1026 of them escape your grasp?
Let Xi be the indicator variable for the event that the i-th molecule is close enough to inhale. We've effectively already used the fact that E[Xi] = 10-4. To use Chebyshev's inequality, we also need Var[Xi] = E[Xi2] - E[Xi]2 = 10-4 - 10-8 ~= 10-4. So the total variance is about 1030*10-4 = 1026 and Chebyshev's inequality says we have Pr[|X - EX| ≥ 1026] ≤ 1026/(1026)2 = 10-26. So death by failure of statistical mechanics is unlikely (and the real probability is much much smaller).
But wait! Even a mere 90% drop in O2 levels is going to be enough to cause problems. What is the probability that this happens? Again we can calculate Pr[90% drop] ≤ Pr[|X-EX| ≥ 0.9*1026] ≤ 1026/(0.9*1026)2 ~= 1.23*10-26. So even temporary asphyxiation by statistical mechanics is not something to worry about.
88. Probability generating functions
For a discrete random variable X taking on only values in ℕ, we can express its distribution using a probability generating function or pgf:
F(z) = ∑ Pr[X=n] zn.
These are essentially standard-issue GeneratingFunctions with the additional requirement that all coefficients are non-negative and F(1) = 1.
A trivial example is the pgf for a Bernoulli random variable (1 with probability p, 0 with probability q=1-p). Here the pgf is just q+pz.
A more complicated example is the pgf for a geometric random variable. Now we have ∑ qk p zk = p ∑ (qz)k = p/(1-qz).
88.1. Sums
A very useful property of pgf's is that the pgf of a sum of independent random variables is just the product of the pgf's of the individual random variables. The reason for this is essentially the same as for ordinary GeneratingFunctions: when we multiply together two terms (Pr[X=n] zn)(Pr[Y=m] zm), we get Pr[X=n ∧ Y=m] zn+m, and the sum over all the different ways of decomposing n+m gives all the different ways to get this sum.
So, for example, the pgf of a binomial random variable equal to the sum of n independent Bernoulli random variables is (q+pz)n (hence the name "binomial").
88.2. Expectation and variance
One nice thing about pgf's is that the can be used to quickly compute expectation and variance. For expectation, we have
F'(z) = ∑ n Pr[X=n] zn-1.
So
- F'(1) = ∑ n Pr[X=n] = E[X].
If we take the second derivative, we get
F''(z) = ∑ n(n-1) Pr[X=n] zn-1
or
F''(1) = ∑ n(n-1) Pr[X=n] = E[X(X-1)] = E[X²] - E[X].
So we can recover E[X²] as F''(1) + F'(1) and get Var[X] as F''(1) + F'(1) - (F'(1))².
- Example
If X is a Bernoulli random variable with pgf F = (q+pz), then F' = p and F'' = 0, giving E[X] = F'(1) = p and Var[X] = F''(1) + F'(1) - (F'(1))² = 0 + p - p² = p(1-p) = pq.
- Example
If X is a binomial random variable with pgf F = (q+pz)n, then F' = n(q+pz)n-1p and F'' = n(n-1)(q+pz)n-2p², giving E[X] = F'(1) = np and Var[X] = F''(1) + F'(1) - (F'(1))² = n(n-1)p² + np - n²p² = np - np² = npq. (These values would, of course, be a lot faster to compute using the formulas for sums of independent random variables, but it's nice to see that they work.)
- Example
If X is a geometric random variable with pgf p/(1-qz), then F' = pq/(1-qz)² and F'' = 2pq²/(1-qz)3. E[X] = F'(1) = pq/(1-q)² = pq/p² = q/p. Var[X] = F''(1) + F'(1) - (F'(1))² = 2pq²/(1-q)3 + q/p - q²/p² = 2q²/p² + q/p - q²/p² = q²/p² + q/p. This would probably be a pain to calculate by hand.
- Example
Let X be a Poisson random variable with rate λ. We claimed earlier that a Poisson random variable is the limit of a sequence of binomial random variables where p = λ/n and n goes to infinity, so (cheating quite a bit) we expect that X's pgf F = lim[n⇒∞] ((1-λ/n) + (λ/n)z)n = (1+(-λ+λz)/n)n = exp(-λ+λz) = exp(-λ) ∑ λnzn/n!. We can check that the total probability F(1) = exp(-λ+λ) = exp(0) = 1, that the expectation F'(1) = λ exp(-λ+λ) = λ, and that the variance F''(1) + F'(1) - (F'(1))² = λ²exp(-λ+λ) + λ - λ² = λ. These last two quantities are what we'd expect if we calculated the expectation and the variance directly as the limit of taking n Bernoulli random variables with expectation λ/n and variance (λ/n)(1-λ/n) each.
89. Summary: effects of operations on expectation and variance of random variables
Operation |
Effect on expectation |
Effect on variance |
Multiplication by a constant |
E[aX] = aE[X] |
Var[aX] = a2 Var[X] |
Addition |
E[X+Y] = E[X] + E[Y]. Does not require independence. |
Var[X+Y] = Var[X] + Var[Y] + 2 Cov(X,Y). Note that Cov(X,Y)=0 if X and Y are independent. |
Product |
E[XY] = E[X]E[Y] + Cov(X,Y). (Or just E[X]E[Y] if X and Y are independent.) |
(No simple formula.) |
90. The general case
So far we have only considered discrete random variables, which avoids a lot of nasty technical issues. In general, a random variable on a probability space (Ω,F,P) is a function whose domain is Ω, which satisfies some extra conditions on its values that make interesting events involving the random variable elements of F. Typically the codomain will be the reals or the integers, although any set is possible. Random variables are generally written as capital letters with their arguments suppressed: rather than writing X(ω), where ω∈Ω, we write just X.
A technical condition on random variables is that the inverse image of any measurable subset of the codomain must be in F—in simple terms, if you can't nail down ω exactly, being able to tell which element of F you land in should be enough to determine the value of X(ω). For a discrete random variables, this just means that X-1(x)∈F for each possible value x. For real-valued random variables the requirement is that the event [X ≤ x] is in F for any fixed x. In each case we say that X is measurable with respect to F (or just "measurable F").11 Usually we will not worry about this issue too much, but it may come up if we are varying F to represent different amounts of information available to different observers (e.g., if X and Y are the values of two dice, X is measurable to somebody who can see both dice but not to somebody who can only see the sum of the dice).
The distribution function of a real-valued random variable describes the probability that it takes on each of its possible values; it is specified by giving a function F(x) = Pr[X ≤ x]. The reason for using Pr[X ≤ x] instead of Pr[X = x] is that it allows specifying continuous random variables such as a random variable that is uniform in the range [0,1]; this random variable has a distribution function given by F(x) = x when 0 ≤ x ≤ 1, F(x) = 0 for x < 0, and F(x) = 1 for x > 1. For discrete random variables the distribution function will have discontinuous jumps at each possible value of the variable; for example, the distribution function of a variable X that is 0 or 1 with equal probability is F(x) = 0 for x < 0, 1/2 for 0 ≤ x < 1, and 1 for x ≥ 1.
Knowing the distribution of a random variable tells you what that variable might do by itself, but doesn't tell you how it interacts with other random variables: for example, if X is 0 or 1 with equal probability then X and 1-X both have the same distribution, but they are connected in a way that is not true for X and some independent variable Y with the same distribution. For multiple variables, a joint distribution gives the probability that each variable takes on a particular value; for example, if X and Y are two independent uniform samples from the range [0,1], their distribution function F(x,y) = Pr[X ≤ x ∧ Y ≤ y] = xy (when 0 ≤ x,y ≤ 1). If instead Y = 1-X, we get the distribution function F(x,y) = Pr[X ≤ x ∧ Y ≤ y] equal to x when y ≥ 1-x and 0 when y < 1-x (assuming 0 ≤ x,y ≤ 1).
We've seen that for discrete random variables, it is more useful to look at the function f(x) = Pr[X=x]. We will often treat such a function as specifying the distribution of X even if it is not technically a distribution function.
90.1. Densities
If a real-valued random variable is continuous in the sense of having a distribution function with no jumps (which means that it has probability 0 of landing on any particular value), we may be able to describe its distribution by giving a density instead. The density is the derivative of the distribution function. We can also think of it as a probability at each point defined in the limit, by taking smaller and smaller regions around the point and dividing the probability of landing in the region by the size of the region.
For example, the density of a uniform [0,1] random variable is f(x) = 1 for x∈[0,1], f(x) = 0 otherwise. For a uniform [0,2] random variable, we get a density of ½ throughout the [0,2] interval. The density always integrates to 1.
Some distributions are easier to describe using densities than using distribution functions. The normal distribution, which is of central importance in statistics, has density
![\[
\frac{1}{\sqrt{2 \pi}} e^{-x^2/2}.
\] \[
\frac{1}{\sqrt{2 \pi}} e^{-x^2/2}.
\]](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_5e8ea4051f531c00d946a6179154e70e667f604e_p1.png)
Its distribution function is the integral of this quantity, which has no closed-form expression.
Joint densities also exist; the joint density of a pair of random variables with joint distribution function F(x,y) is given by the partial derivative f(x,y) = ∂²/∂x∂y F(x,y). The intuition here again is that we are approximating the (zero) probability at a point by taking the probability of a small region around the point and dividing by the area of the region.
90.2. Independence
Independence is the same as for discrete random variables: Two random variables X and Y are independent if any pair of events of the form X∈A, Y∈B are independent. For real-valued random variables it is enough to show that their joint distribution F(x,y) is equal to the product of their individual distributions FX(x)FY(y). For real-valued random variables with densities, showing the densities multiply also works. Both methods generalize in the obvious way to sets of three or more random variables.
90.3. Expectation
If a continuous random variable has a density f(x), the formula is
![\[
\E[X] = \int x f(x) dx.
\] \[
\E[X] = \int x f(x) dx.
\]](/pinewiki/RandomVariables?action=AttachFile&do=get&target=latex_e535e19fe5d90cc3a9f9dc27bf26a7093f4b0d9f_p1.png)
For continuous random variables without densities we land in a rather swampy end of integration theory. We will not talk about this case if we can help it. But in each case the expectation depends only on the distribution of X and not on its relationship to other random variables.
- Example (continuous variable with density)
Let X be a uniform random variable in the range [a,b]. Then E[X] = ∫[a,b] x 1/(b-a) dx = (1/(b-a))(x²/2)|x=a..b = (1/(b-a))(b²/2 - a²/2) = (b+a)/2.
91. Relations
Contents
92. Relations, digraphs, and matrices
A binary relation from a set A to a set B is a subset of A×B. In general, an n-ary relation on sets A1, A2, ..., An is a subset of A1×A2×...×An. We will mostly be interested in binary relations, although n-ary relations are important in databases; unless otherwise specified, a relation will be a binary relation. A relation from A to A is called a relation on A; many of the interesting classes of relations we will consider are of this form. Some simple examples are the relations =, <, and ≤ on the integers.
You may recall that functions are a special case of relations (see Functions), but most of the relations we will consider now will not be functions.
Binary relations are often written in infix notation: instead of writing (x,y)∈R, we write xRy. This should be pretty familiar for standard relations like < but might look a little odd at first for relations named with capital letters.
92.1. Directed graphs
Relations are one of several structures over pairs of objects. Another such structure is a directed graph, consisting of a set of vertices V and a set of edges E, where each edge E has an initial vertex init(e) and a terminal vertex term(E). A simple directed graph has no "parallel edges": there are no edges e1 and e2 with init(e1) = init(e2) and term(e1) = term(e2).
If we don't care about the labels of the edges, a simple directed graph can be described by giving E as a subset of V×V; this gives a one-to-one correspondence between relations on a set V and (simple) directed graphs. For relations from A to B, we get a bipartite directed graph, where all edges go from vertices in A to vertices in B.
Directed graphs are drawn using a dot for each vertex and an arrow for each edge, like so:
This also gives a way to draw relations. For example, the relation on { 1, 2, 3 } given by { (1,2), (1,3), (2,3), (3,1) } would look like this:
92.2. Matrices
A matrix is a two-dimensional analog of a sequence: in full generality, it is a function A:S×T→U, where S and T are the index sets of the matrix (typically { 1..n } and {1..m} for some n and m). As with sequences, we write Aij for A(i,j). Matrices are typically drawn inside square brackets like this:
![\[
A =
\left[
\begin{array}{rrrr}
0 & 1 & 1 & 0 \\
2 & 1 & 0 & 0 \\
1 & 0 & 0 & -1
\end{array}
\right].
\] \[
A =
\left[
\begin{array}{rrrr}
0 & 1 & 1 & 0 \\
2 & 1 & 0 & 0 \\
1 & 0 & 0 & -1
\end{array}
\right].
\]](/pinewiki/Relations?action=AttachFile&do=get&target=latex_4769f5af28d15413bc2ffd5e070d5f396d07eac7_p1.png)
The first index of an entry gives the row it appears in and the second one the column, so in this example A1 2 = 2 and A3 4 = -1. The dimensions of a matrix are the numbers of rows and columns; in the example, A is a 3×4 (pronounced "3 by 4") matrix.
Matrices are used heavily in LinearAlgebra, but for the moment we will use them to represent relations from { 1..n } to { 1..m }, by setting Aij = 0 if (i,j) is not in the relation and Aij = 1 if (i,j) is. So for example, the relation on { 1..3 } given by { (i,j) | i < j } would appear in matrix form as
![\[
\left[
\begin{array}{rrr}
0 & 1 & 1 \\
0 & 0 & 1 \\
0 & 0 & 0 \\
\end{array}
\right].
\] \[
\left[
\begin{array}{rrr}
0 & 1 & 1 \\
0 & 0 & 1 \\
0 & 0 & 0 \\
\end{array}
\right].
\]](/pinewiki/Relations?action=AttachFile&do=get&target=latex_1ae20543d466d707fe8cb53875de750e0dcdeb24_p1.png)
93. Operations on relations
93.1. Composition
Just like functions, relations can be composed: given R:A→B and S:B→C we define (S∘R):A→C by the rule (x,z)∈(S∘R) if and only if there exists some y∈B such that (x,y)∈R and (y,z)∈S. (In infix notation: x(S∘R)z ⇔ ∃y xRy ∧ ySz.) It's not hard to see that ordinary function composition is just a special case of relation composition.
In matrix terms, composition acts like matrix multiplication, where we replace scalar multiplication with AND and scalar addition with OR: (S∘R)ij = ∨k (Rik∧Skj). Note that if we use the convention that Rij = 1 if iRj the order of the product is reversed from the order of composition.
For relations on a single set, we can iterate composition: Rn is defined by R0 = (=) and Rn+1 = R∘Rn. (This also works for functions.) In directed graph terms, xRny iff there is a path of exactly n edges from x to y (possibly using the same edge more than once).
93.2. Inverses
Relations also have inverses: xR-1y ⇔ yRx. Unlike functions, every relation has an inverse.
94. Classifying relations
Certain properties of relations on a set are important enough to be given names that you should remember.
- Reflexive
A relation R on a set A is reflexive if (a,a) is in R for all a in A. The relations = and ≤ are both reflexive. The equality relation is in a sense particularly reflexive: a relation R is reflexive if and only if it is a superset of =.
- Symmetric
A relation R is symmetric if (a,b) is in R whenever (b,a) is. Equality is symmetric, but ≤ is not. Another way to state symmetry is that R = R-1.
- Antisymmetric
A relation R is antisymmetric if the only way that both (a,b) and (b,a) can be in R is if a=b. (More formally: aRb ∧ bRa ⇒ a=b.) The "less than" relation < is antisymmetric: if a is less than b, b is not less than a, so the premise of the definition is never satisfied. The "less than or equal to" relation ≤ is also antisymmetric; here it is possible for a≤b and b≤a to both hold, but only if a=b. The set-theoretic statement is R is symmetric iff R∩R-1⊆(=). This is probably not as useful as the simple definition.
- Transitive
A relation R is transitive if (a,b) in R and (b,c) in R implies (a,c) in R. The relations =, <, and ≤ are all transitive. The relation { (x,x+1) | x in ℕ } is not. The set-theoretic form is that R is transitive if R²⊆R, or in general if Rn⊆R for all n > 0.
95. Equivalence relations
An equivalence relation is a relation that is reflexive, symmetric, and transitive. Equality is the model of equivalence relations, but some other examples are:
- Equality mod m: The relation x = y (mod m) that holds when x and y have the same remainder when divided by m is an equivalence relation.
Equality after applying a function: Let f:A→B be any function, and define x ~f y if f(x) = f(y). Then ~f is an equivalence relation.
Membership in the same block of a partition: Let A be the union of a collection of sets Ai where the Ai are all disjoint. The set { Ai } is called a partition of A and each individual set Ai is called a block of the partition. Let x ~ y if x and y appear in the same block Ai for some i. Then ~ is an equivalence relation.
Directed graph isomorphism: Suppose that G=(V,E) and G'=(V',E') are directed graphs, and there exists a bijection f:V→V' such that (u,v) is in E if and only if (f(u), f(v)) is in E'. Then G and G' are said to be isomorphic (from Greek "same shape"). The relation G ≅ G' that holds when G and G' are isomorphic is easily seen to be reflexive (let f by the identity function), symmetric (replaced f by f-1), and transitive (compose f:G→G' and g:G'→G''); thus it is an equivalence relation.
Partitioning a plane: draw a curve in a plane (i.e., pick a continuous function f:[0,1]→R2). Let x~y if there is a curve from x to y (i.e., a curve g with g(0) = x and g(1) = y) that doesn't intersect the first curve. Then x~y is an equivalence relation on points in the plane excluding the curve itself. Proof: To show x~x, let g be the constant function g(t) = x. To show x~y ↔ y~x, consider some function g with g(0) = x and g(1) = y and let g'(t) = g(1-t). To show x~y and y~z ⇒ x~z, let g be a curve from x to y and g' a curve from y to z, and define a new curve (g+g') by (g+g')(t) = g(2t) when t ≤ 1/2 and (g+g')(t) = g'(2t-1) when t ≥ 1/2.
Any equivalence relation ~ on a set A gives rise to a set of equivalence classes, where the equivalence class of an element a is the set of all b such that a ~ b. Because of transitivity, the equivalence classes form a partition of the set A, usually written A/~ (prounounced "A slash ~" or sometimes "A modulo ~"). A member of a particular equivalence class is said to be a representative of that class. For example, the equivalence classes of equality mod m are the sets Ai = { i + km } with representatives { 0, 1, 2, 3, ..., m - 1 }. A more complicated case are the equivalence classes of the plane partitioning example; here the equivalence classes are essentially the pieces we get after cutting out the curve f, and any point on a piece can act as a representative for that piece.
95.1. Why we like equivalence relations
Equivalence relations are the way that mathematicians say "I don't care." If you don't care about which integer you've got except for its remainder when divided by m, then you define two integers that don't differ in any way that you care about to be equivalent and work in ℤ/~ (ℤ/(= mod m) in this case). This turns out to be incredibly useful for defining new kinds of things: for example, we can define multisets (sets where elements can appear more than once) by starting with sequences, declaring x~y if there is a permutation of x that reorders it into y, and then defining a multiset as an equivalence class with respect to this relation.
This can also be used informally: "I've always thought that brocolli, spinach, and kale are in the same equivalence class."12
96. Partial orders
A partial order is a relation ≤ that is reflexive and transitive, and antisymmetric: the last means that if x ≤ y and y ≤ x, then x = y. A set S together with a partial order ≤ is called a partially ordered set or poset. A strict partial order is a relation < that is irreflexive and transitive (which implies antisymmetry as well). Any partial order ≤ can be converted into a strict partial order and vice versa by deleting/including the pairs (x,x) for all x.
Examples:
- (ℕ, ≤) is a poset.
(ℕ, ≥) is also a poset. In general, if R is a partial order, then R-1 is also a partial order.
The divisibility relation a|b on natural numbers, where a|b if and only if there is some k in ℕ such that b = ak, is reflexive (let k = 1), antisymmetric (if a|b then a≤b so if a|b and b|c then a≤b and b≤c implying a=b) and transitive (if b = ak and c = bk' then c = akk'). Thus it is a partial order.
Let (A,≤A) and (B,≤B) be posets. Then the relation ≤ on A×B defined by (a,b) ≤ (a',b') iff a ≤ a' and b ≤ b' is a partial order. The poset (A×B,≤) defined in this way is called the product poset of A and B.
Again let (A,≤A) and (B,≤B) be posets. The relation ≤ on A×B defined by (a,b) ≤ (a',b') if a < a' or a = a' and b ≤ b' is called lexicographic order on A×B and is a partial order. The useful property of lexicographic order (lex order for short) is that if the original partial orders are total, so is the lex order: this is why dictionary-makers use it. This also gives a source of very difficult-to-visualize total orders, like lex order on ℝ×ℝ, which looks like the classic real number line where every point is replaced by an entire copy of the reals.
Let Σ be some alphabet and consider the set Σ* = Σ0∪Σ1∪Σ2... of all finite words drawn from Σ. Given two words x and y, let x≤y if x is a prefix of y, i.e. if there is some word z such that xz=y. Then (Σ*,≤) is a poset.
Using the same set Σ*, let x⊑y if x is a subsequence of y, i.e., if there is a sequence of increasing positions i1, i2, ... ik such that xj = yij. (For example, bd⊑abcde.) Then (Σ*,⊑) is a poset.
There are also some common relations that are not partial orders or strict partial orders but come close. For example, the element-of relation (∈) is irreflexive and antisymmetric (this ultimately follows from the Axiom of Foundation) but not transitive; if x∈y and y∈z we do not generally expect x∈z. The "is at least as rich as" relation is reflexive and transitive but not antisymmetric: if you and I have a net worth of 0, we are each as rich as the other, and yet we are not the same person. Relations that are reflexive and transitive (but not necessarily antisymmetric) are called quasiorders or preorders and can be turned into partial orders by replacing each set of elements for which x≤y and y≤x for all elements in the set by a single element. (As far as I know there is no standard term for relations that are irreflexive and antisymmetric but not necessarily transitive.)
96.1. Drawing partial orders
Since partial orders are relations, we can draw them as directed graphs. But for many partial orders, this produces a graph with a lot of edges whose existence is implied by transitivity, and it can be easier to see what is going on if we leave the extra edges out. If we go further and line the elements up so that x is lower than y when x < y, we get a Hasse diagram: a representation of a partially ordered set as a graph where there is an edge from x to y if x < y and there is no z such that x < z < y. (There is special terminology for this situation: such an x is called a predecessor or sometimes immediate predecessor of y; y in turn is the successor or sometimes immediate successor of x.)
Here is an example of a Hasse diagram on a partially-ordered set with 5 elements. Observe that the full relation (depicted on the right) is much more tangled than the Hasse diagram. The red edges are those whose existence is implied by transitivity.
96.2. Comparability
In a partial order, two elements x and y are comparable if x≤y or y≤x. Elements that are not comparable are called incomparable. In a Hasse diagram, comparable elements are connected by a path that only goes up. For example, in the partial order whose Hasse diagram was given earlier, all elements are comparable to each other except the two elements at the top.
96.3. Minimal and maximal elements
If for some x there is no y < x, x is minimal. A partial order may have any number of minimal elements: e.g. the integers have no minimal element, the naturals have one minimal element, a set with k elements none of which are comparable to each other has k minimal elements. If an element x is not only minimal but also satisfies x < y for all y not equal to x, then x is a minimum. A partial order may have at most one minimum (e.g. 0 in the naturals), but may have no minimum, either because it has no minimal elements to begin with or because it has more than one.
The corresponding terms for elements that are not less than any other element or greater than all other elements are maximal and maximum, respectively.
Here is an example of the difference between a maximal and a maximum element: consider the family of all subsets of ℕ with at most three elements, ordered by ⊆. Then {0,1,2} (or any other three-element set) is a maximal element of this family (it's not a subset of any larger set), but it's not a maximum because it's not a superset of e.g. {3}.
96.4. Total orders
If any two elements of a partial order are comparable (i.e., if at least one of x≤y or y≤x holds for all x,y), then the partial order is a total order. Total orders include many of the familiar orders on the naturals, the reals, etc.
Any partial order (S,<) can be extended to a total order (generally more than one, if the partial order is not total itself). The essential idea is to break ties between incomparable elements in a way that is consistent with maintaining transitivity. For finite partial orders this can be done by starting with some minimal element and declaring it to be the minimum, and then repeating with the elements that are left. (This process is called a TopologicalSort, and there are fast algorithms for it.)
For infinite partial orders the situation is more complicated. The intuition is that we can always pick some pair of incomparable elements and declare one less than the other, fill in any other relations implied by transitivity, and repeat. Unfortunately this process may take infinitely long, so we have to argue that it converges in the limit to a genuine total order using a tool called Zorn's lemma, which itself is a theorem about partial orders.13
96.5. Well orders
A well order is a particularly restricted kind of total order. A partial order is a well order if it is a total order and, for every nonempty subset S, S contains some minimum element x: one that is less than or equal to all elements of S. An example of a well order is the usual order on ℕ.14
An equivalent definition is that a total order is a well order if it contains no infinite descending chains, which are infinite sequences x1, x2, ... with x1 > x2 > x3 > ... . To show that this is implied by every set having a least element, suppose that a given total order has the least-element property. Then given a would-be infinite descending chain x1, x2, ..., let xi be its least element. But then xi is not greater than xi+1. For the converse, suppose that some set S does not have a least element. Then we can construct an infinite descending chain by choosing any x1 in S, then for each xi+1 choose some element less than the smallest of x1...xi. (Note: iterating this process forever requires using the Axiom of Choice. Bizarre things happen in order theory without the Axiom of Choice.)
The useful property of well-orders is that we can do induction on them. If it is the case that (a) P(m) holds, where m is the smallest element in some set S, and (b) P(x') for all x < x' implies P(x); then P(x) holds for all x in S. The proof is that if P(x) doesn't hold, there is a least element y in S for which it doesn't hold. But this contradicts (a) if y=m and (b) otherwise. This assumes, of course, that the < relation is a well-order, because otherwise m may not exist. (For example, we can't do induction on the integers because there is no number negative enough to be the base case).
It is possible in an infinite set to have a well-ordering in which some elements do not have predecessors. For example, the order on S = ℕ ∪ { ω } defined by x ≤ y if either (a) x and y are both in ℕ and x ≤ y by the usual ordering on ℕ or (b) y = ω is a total order that is also a well order, but ω has no immediate predecessor. In this case we can still do induction proofs, but since ω is not n+1 for any n we need a special case in the proof to handle it. For a more complicated example, the set ω+ω = { 0, 1, 2, ...; ω, ω+1, ω+2, ... } is also well-ordered, so we can do induction on it if we can show P(0), P(x) ⇒ P(x+1), and P(ω) (possibly using P(x) for all x < ω in the last case).
96.6. Lattices
A lattice is a partial order in which (a) each pair of elements x and y has a unique greatest lower bound or meet, written x∧y, with the property that (x∧y)≤x, (x∧y)≤y, and z≤(x∧y) for any z with z≤x and z≤y; and (b) each pair of elements x and y has a unique least upper bound or join, written x∨y, with the property that (x∨y)≥x, (x∨y)≥y, and z≥(x∨y) for any z with z≥x and z≥y.
Examples of lattices are any total order (x∧y is min(x,y), x∨y is max(x,y)), the subsets of a fixed set ordered by inclusion (x∧y is x∩y, x∨y is x∪y), and the divisibility relation on the positive integers (x∧y is the greatest common divisor, x∨y is the least common multiple—see NumberTheory). Products of lattices with the product order15 are also lattices: (x₁,x₂)∧(y₁,y₂) = (x₁∧₁y₁,x₂∧y₂) and (x₁,x₂)∨(y₁,y₂) = (x₁∨₁y₁,x₂∨y₂).
97. Closure
In general, the closure of some mathematical object with respect to a given property is the smallest larger object that has the property. Usually "smaller" and "larger" are taken to mean subset or superset, so we are really looking at the intersection of all larger objects with the property. Such a closure always exists if the property is preserved by intersection (i.e., if (∀i P(Si)) ⇒ P(∩Si)) and every object has at least one larger object with the property.
This rather abstract definition can be made more explicit for certain kinds of closures of relations. The reflexive closure of a relation R (whose domain and codomain are equal) is the smallest super-relation of R that is reflexive; it is obtained by adding (x,x) to R for all x in R's domain. The symmetric closure is the smallest symmetric super-relation of R; it is obtained by adding (y,x) to R whenever (x,y) is in R, or equivalently by taking R∪R-1. The transitive closure is obtained by adding (x,z) to R whenever (x,y) and (y,z) are both in R for some y—and continuing to do so until no new pairs of this form remain. The transitive closure can also be computed as R1∪R2∪R3...; for reflexive R, this is equal to R0∪R1∪R2..., which is often written as R*.
In digraph terms, the reflexive closure adds self-loops to all nodes, the symmetric closure adds a reverse edge for each edge, and the transitive closure adds an edge for each directed path through the graph. One can also take the closure with respect to multiple properties, such as the reflexive symmetric transitive closure of R which will be the smallest equivalence relation in which any elements that are related by R are equivalent.
Closures provide a way of turning things that aren't equivalence relations or partial orders into equivalence relations and partial orders. For equivalence relations this is easy: take the reflexive symmetric transitive closure, and you get a reflexive symmetric transitive relation. For partial orders it's trickier: antisymmetry isn't a closure property (even though it's preserved by intersection, a non-antisymmetric R can't be made anti-symmetric by adding more pairs). Given a relation R on some set S, the best we can do is take the reflexive transitive closure R* and hope that it's antisymmetric. If it is, we are done. If it isn't, we can observe that the relation ~ defined by x~y if xR*y and yR*x is an equivalence relation (proof: x~x because R* is reflexive, x~y ⇒ y~x from the symmetry of the definition, and x~y ∧ y~z ⇒ x~z because transitivity of R* gives xR*y ∧ yR*z ⇒ xR*z and yR*x and zR*y ⇒ zR*x). So we can take the quotient S/~, which smashes all the equivalence classes of ~ into single points, define a quotient relation R*/~ in the obvious way, and this quotient relation will be a partial order.
97.1. Examples
Let R be the relation on subsets of ℕ given by xRy if there exists some n∉x such that y = x∪{n}. The transitive closure of R is the proper subset relation ⊂, where x⊂y if x⊆y but x≠y; the reflexive transitive closure R* of R is just the ordinary subset relation ⊆. The reflexive symmetric transitive closure of R is the complete relation; given any two sets x and y, we can get from x to ∅ via (R*)-1 and then to y via R*. So in this case the reflexive symmetric transitive closure is not very interesting.
Let R be the relation on ℕ given by xRy if x=2y. Then the reflexive transitive closure R* is the relation given by xR*y if x=2ny for some n∈ℕ, and the reflexive symmetric transitive closure is the relation given by x~y if x=2ny or y=2nx for some n∈ℕ. For this R not all elements of the underlying set are equivalent in the reflexive symmetric transitive closure; instead, we get a separate equivalence class { k, 2k, 4k, 8k, ... } for each odd number k.
98. GraphTheory
A graph is a structure in which pairs of vertices are connected by edges. Each edge may act like an ordered pair (in a directed graph) or an unordered pair (in an undirected graph). We've already seen directed graphs as a representation for Relations; but most work in graph theory concentrates instead on undirected graphs.
Because graph theory has been studied for many centuries in many languages, it has accumulated a bewildering variety of terminology, with multiple terms for the same concept (e.g. node for vertex or arc for edge) and ambiguous definitions of certain terms (e.g., a "graph" without qualification might be either a directed or undirected graph, depending on who is using the term: graph theorists tend to mean undirected graphs, but you can't always tell without looking at the context). We will try to stick with consistent terminology to the extent that we can. In particular, unless otherwise specified, a graph will refer to a simple undirected graph: an undirected graph where each edge connects two distinct vertices (thus no self-loops) and there is at most one edge between each pair of vertices (no parallel edges).
Reasonably complete glossaries of graph theory can be found at http://www-leibniz.imag.fr/GRAPH/english/definitions.html or Glossary of graph theory. See also RosenBook Chapter 9, or BiggsBook Chapter 15 (for undirected graphs) and 18 (for directed graphs).
If you want to get a sense of the full scope of graph theory, Reinhard Diestel's (graduate) textbook Graph Theory can be downloaded from http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/download.html.
99. Types of graphs
Graphs are represented as ordered pairs G = (V,E), where V is a set of vertices and E a set of edges. The differences between different types of graphs depends on what can go in E. When not otherwise specified, we usually think of a graph as an undirected graph (see below), but there are other variants.
99.1. Directed graphs
In a directed graph or digraph, each element of E is an ordered pair, and we think of edges as arrows from a source, head, or initial vertex to a sink, tail, or terminal vertex; each of these two vertices is called an endpoint of the edge. A directed graph is simple if there is at most one edge from one vertex to another. A directed graph that has multiple edges from some vertex u to some other vertex v is called a directed multigraph.
As we saw in Relations, there is a one-to-one correspondence between simple directed graphs with vertex set V and relations on V.
99.2. Undirected graphs
In an undirected graph, each edge is a two-element subset of V. A simple undirected graph contains no duplicate edges and no loops (an edge from some vertex u back to itself). A graph with more than one edge between the same two vertices is called a multigraph. Most of the time, when we say graph, we mean a simple undirected graph.
Some authors make a distinction between pseudographs (with loops) and multigraphs (without loops), but we'll use multigraph for both.
Simple undirected graphs also correspond to relations, with the restriction that the relation must be irreflexive (no loops) and symmetric (undirected edges). This also gives a representation of undirected graphs as directed graphs, where the edges of the directed graph always appear in pairs going in opposite directions.
99.3. Hypergraphs
In a hypergraph, the edges (called hyperedges) are arbitrary nonempty sets of vertices. A k-hypergraph is one in which all such hyperedges connected exactly k vertices; an ordinary graph is thus a 2-hypergraph.
Hypergraphs are usually drawn by representing each hyperedge as a closed curve containing its members, like so:
Hypergraphs aren't used very much, because it is always possible (though not always convenient) to represent a hypergraph by a bipartite graph. In a bipartite graph, the vertex set can be partitioned into two subsets S and T, such that every edge connects a vertex in S with a vertex in T. To represent a hypergraph H as a bipartite graph, we simply represent the vertices of H as vertices in S and the hyperedges of H as vertices in T, and put in an edge (s,t) whenever s is a member of the hyperedge t in H. (See also BipartiteGraphs.)
100. Examples of graphs
Any relation produces a graph, which is directed for an arbitrary relation and undirected for a symmetric relation. Examples are graphs of parenthood (directed), siblinghood (undirected), handshakes (undirected), etc.
Graphs often arise in transportation and communication networks. Here's a (now somewhat out-of-date) route map for Jet Blue airlines, taken from http://www.jetblue.com/travelinfo/routemap.html:
Such graphs are often labeled with edge lengths, prices, etc. In computer networking, the design of network graphs that permit efficient routing of data without congestion, roundabout paths, or excessively large routing tables is a central problem.
The web graph is a directed multigraph with web pages for vertices and hyperlinks for edges. Though it changes constantly, its properties have been fanatically studied both by academic graph theorists and employees of search engine companies, many of which are still in business. Companies such as Google base their search rankings largely on structural properties of the web graph.
Peer-to-peer systems for data sharing often have a graph structure, where each peer is a node and connections between peers are edges. The problem of designing efficient peer-to-peer systems is similar in many ways to the problem of designing efficient networks; in both cases, the structure (or lack thereof) of the underlying graph strongly affects efficiency.
101. Graph terminology
Incidence: a vertex is incident to any edge of which it is an endpoint (and vice versa).
Adjacency, neighborhood: two vertices are adjacent if they are the endpoints of some edge. The neighborhood of a vertex v is the set of all vertices that are adjacent to v.
Degree, in-degree, out-degree: the degree of v counts the number edges incident to v. In a directed graph, in-degree counts only incoming edges and out-degree counts only outgoing edges (so that the degree is always the in-degree plus the out-degree). The degree of a vertex v is often abbreviated as d(v) or δ(v); in-degree and out-degree are sometimes abbreviated as d-(v) and d+(v), respectively (or δ-(v) and δ+(v) by people who prefer Greek).
102. Some standard graphs
Complete graph Kn. This has n vertices, and every pair of vertices has an edge between them.
Cycle graph Cn. This has vertices {0, 1, ... n-1} and an edge from i to i+1 for each i, plus an edge from n-1 to 0. Here n must be at least 3 to get a simple graph.
Path Pn. This has vertices {0, 1, 2, ... n} and an edge from i to i+1 for each i. Note that n counts the number of edges rather than the number of vertices; we call the number of edges the length of the path.
Complete bipartite graph Kmn. This has a set A of m vertices and a set B of n vertices, with an edge between every vertex in A and every vertex in B, but no edges within A or B.
Star graphs. These have a single central vertex that is connected to n outer vertices, and are the same as K1n.
The cube Qn. This is defined by letting the vertex set consist of all n-bit strings, and putting an edge between u and u' if u and u' differ in exactly one place. It can also be defined by taking the n-fold square product of an edge with itself (see below).
Cayley graphs. The Cayley graph of a group G with a given set of generators is a labeled directed graph. The vertices of this graph are the group elements, and for each g in G and s in S there is a directed edge from g to gs labeled with s. Many common graphs are Cayley graphs with the labels (and possibly edge orientations) removed; for example, a directed cycle on m elements is the Cayley graph of ℤm, an n×m torus is the Cayley graph of ℤn×ℤm, and the cube Qn is the Cayley graph of (ℤ2)n.
Graphs may not always be drawn in a way that makes their structure obvious. For example, here are two different presentations of Q3, only one of which looks much like a cube:
103. Operations on graphs
- Set-like operations
Subgraphs: G is a subgraph of H, written G ⊆ H, if VG ⊆ VH and EG ⊆ EH.
- One can get subgraphs by deleting edges or vertices or both. Note that deleting a vertex also requires deleting any edges incident to the vertex (since we can't have an edge with a missing endpoint).
The maximal subgraph of a graph H whose vertex set is S is called the induced subgraph of H with vertices S. The intuition is that all edges are left in whose endpoints lie in S.
- We will sometimes say that G is a subgraph of H if it is isomorphic to a subgraph of H, which is equivalent to having an injective homomorphism from G to H.
- Intersections and unions are defined in the obvious way. The only tricky part is that with intersections we need to think a bit to realize this doesn't produce edges with missing endpoints.
- Products. There are at least five different definitions of the product of two graphs used by serious graph theorists. In each case the vertex set of the product is the Cartesian product of the vertex sets, but the different definitions throw in different sets of edges. Two of them are used most often:
Square product (graph Cartesian product) G ◻ H. An edge (u,u')(v,v') is in G ◻ H if and only if (a) u=v and u'v' is an edge in H, or (b) uv is an edge in G and v=v'. Called the square product because the product of two (undirected) edges looks like a square. The intuition is that each vertex in G is replaced by a copy of H, and then corresponding vertices in the different copies of H are linked whenever the original vertices in G are adjacent. For algebraists, square products are popular because they behave correctly for Cayley graphs: if C1 and C2 are the Cayley graphs of G1 and G2 (for particular choices of generators), then C1 ◻ C2 is the Cayley graph of G1×G2.
The cube Qn can be defined recursively by Q1 = P1 and Qn = Qn-1◻Q1. It is also the case that Qn=Qk◻Qn-k.
An n-by-m mesh is given by Pn-1◻Pm-1.
- Cross product (categorical graph product) G × H. Now (u,u')(v,v') is in G × H if and only if uv is in G and u'v' is in H. In the cross product, the product of two (again undirected) edges is a cross: an edge from (u,u') to (v,v') and one from (u,v') to (v,u'). The cross product is not as useful as the square product for defining nice-looking graphs, but it can arise in some other situations. An example is when G and H describe the positions (vertices) and moves (directed edges) of two solitaire games; then the cross product G × H describes the combined game in which at each step the player must make a move in both games. (In contrast, the square product G ◻ H describes a game where the player can choose at each step to make a move in either game.)
Graph powers, transitive closures: see Connectivity below.
- Minors.
A minor of a graph G is some other graph H obtained from G by deleting edges and/or vertices (as in a subgraph) and contracting edges, where two adjacent vertices u and v are merged together into a single vertex that is connected to all of the previous neighbors of both vertices.
Minors are useful for recognizing certain classes of graphs. For example, a graph can be drawn in the plane without any crossing edges if and only if it doesn't contain K5 or K3,3 as a minor (this is known as Wagner's theorem).
- Functions from one graph to another.
Isomorphisms: If f:VG→VH is a bijection and uv ∈ EG if and only if f(u)f(v) ∈ EG, then G and H are said to be isomorphic and f is an isomorphism. Isomorphism is an equivalence relation—using it, we can divide graphs into equivalence classes and effectively forget the identities of the vertices. We don't currently know how to test whether two graphs are isomorphic (the Graph isomorphism problem); at the same time, we also don't know that testing isomorphism is hard, even assuming P≠NP. Graph isomorphism is a rare example of a natural problem for which we have neither a good algorithm nor a hardness proof.
Automorphism: An isomorphism from G to G is called an automorphism of G. Automorphisms correspond to internal symmetries of a graph. For example, the cycle Cn has 2n different automorphisms (to count them, observe there are n places we can send vertex 0 to, and having picked a place to send vertex 0 to, there are only 2 places to send vertex 1; so we have essentially n rotations times 2 for flipping or not flipping the graph). A path Pn has only 2 automorphisms (reverse the direction or not). Many graphs have no automorphisms except the identity map.
Homomorphisms: a homomorphism f from a graph G = (VG, EG) to a graph H = (VH, EH) is a function f:VG→VH such that, for all uv in EG, f(u)f(v) is in EH. (This definition assumes no parallel edges, but otherwise works for both directed and undirected graphs.) These are probably only of interest to category theorists.
- Intuition: a homomorphism is a function from vertices of G to vertices of H that also maps edges to edges.
- Example: There is a unique homomorphism from the empty graph (Ø,Ø) to any graph.
Example: Let G = (V,E) be an undirected graph. Then there are exactly 2 homomorphisms from P1 to G for each edge in G.
Example: There is a homomorphism from G to P1 if and only if G is bipartite. In general, there is a homomorphism from G to Kn if and only if G is n-partite (recall P1 = K2).
Comment: For multigraphs, one must define a homomorphism as a pair of functions fV:VG→VH and fE:EG→EH with appropriate consistency conditions.
104. Paths and connectivity
A fundamental property of graphs is connectivity: whether the graph can be divided into two or more pieces with no edges between them. Often it makes sense to talk about this in terms of reachability, or whether you can get from one vertex to another along some path.
A path of length n in a graph is the image of a homomorphism from Pn.
In ordinary speech, it's a sequence of n+1 vertices v0, v1, ..., vn such that vivi+1 is an edge in the graph for each i.
A path is simple if the same vertex never appears twice (i.e. if the homomorphism is injective). If there is a path from u to v, there is a simple path from u to v obtained by removing cycles.
If there is a path from u to v, then v is reachable from u: u →* v. We also say that u is connected to v.
- Easy to see that connectivity is reflexive (take a path of length 0) and transitive (paste a path from u to v together with a path from v to w to get a path from u to w). But it's not necessarily symmetric if we have a directed graph.
- Connected components
In an undirected graph, connectivity is symmetric, so it's an equivalence relation.
Equivalence classes of →* are called the connected components of G.
G itself is connected iff it has a single connected component, i.e. if every vertex is reachable from every other vertex.
- Note that isolated vertices count as (separate) connected components.
- In a directed graph, we can make connectivity symmetric in one of two different ways:
Define u to be strongly connected to v if u →* v and v →* u. I.e. u and v are strongly connected if you can go from u to v and back again (not necessarily through the same vertices).
- Easy to see that strong connectivity is an equivalence relation.
Equivalence class are called strongly-connected components.
G is strongly connected if it has one strongly-connected component, i.e. if every vertex is reachable from every other vertex.
Define u to be weakly connected to v if u →* v in the undirected graph obtained by ignoring edge orientation.
- Intuition is that u is weakly connected to v if there is a path from u to v if you are allowed to cross edges backwards.
- Weakly-connected components are defined by equivalence classes; graph is weakly-connected if it has one component.
- Weak connectivity is a "weaker" property that strong connectivity in the sense that if u is strongly connected to v, then u is weakly connected to v; but the converse does not necessarily hold.
Power of a directed graph: k-th power Gk has same vertices as G, but uv is an edge in Gk if and only if there is a path of length k from u to v in G.
Transitive closure of a directed graph: <
 >. I.e. there is an edge uv in G* iff there is a path (of any length, including zero) from u to v in G, or in other words if u →* v.
>. I.e. there is an edge uv in G* iff there is a path (of any length, including zero) from u to v in G, or in other words if u →* v. Application of powers and transitive closure of a relation, defined by Rk = R ∘ R ∘ ... R (k times) and R* = union of Rk for all k. So →* is the transitive closure of the directed adjacency relation →.
105. Cycles
The standard cycle graph Cn has vertices {0, 1, ..., n-1} with an edge from i to i+1 for each i and from n-1 to 0. A cycle of length n in a graph G is an image of Cn under homomorphism which includes each edge at most once. A simple cycle is a cycle that includes each vertex at most once. Cycles are often written by giving their sequence of vertices v0v1v2...vkv0, where there is an edge from each vertex in the sequence to the following vertex. Unlike paths, which have endpoints, no vertex in a cycle has a special role.
A graph with no cycles is acyclic. Directed acyclic graphs or DAGs have the property that their reachability relation →* is a partial order; this is easily proven by showing that if →* is not anti-symmetric, then there is a cycle consisting of the paths between two non-anti-symmetric vertices u →* v and v →* u. Directed acyclic graphs may also be topologically sorted: their vertices ordered as v0, v1, ..., vn-1, so that if there is an edge from vi to vj, then i < j. The proof is by induction on |V|, with the induction step setting vn-1 to equal some vertex with out-degree 0 and ordering the remaining vertices recursively. (See also TopologicalSort.)
Connected acyclic undirected graphs are called trees. A connected graph G = (V,E) is a tree if and only if |E|=|V|-1; we'll prove this below.
A cycle that includes every edge exactly once is called an Eulerian cycle or Eulerian tour, after Leonhard Euler, whose study of the Seven bridges of Königsberg problem led to the development of graph theory. A cycle that includes ever vertex exactly once is called a Hamiltonian cycle or Hamiltonian tour, after William Rowan Hamilton, another historical graph-theory heavyweight (although he is more famous for inventing quaternions and the Hamiltonian). Graphs with Eulerian cycles have a simple characterization: a graph has an Eulerian cycle if and only if every vertex has even degree. Graphs with Hamiltonian cycles are harder to recognize.
106. Proving things about graphs
Suppose we want to show that all graphs or perhaps all graphs satisfying certain criteria have some property. How do we do this? In the ideal case, we can decompose the graph into pieces somehow and use induction on the number of vertices or the number of edges. If this doesn't work, we may have to look for some properties of the graph we can exploit to construct an explicit proof of what we want.
106.1. The Handshaking Lemma
This lemma relates the total degree of a graph to the number of edges. Observe that δ(v) = #{u: uv ∈ E} = ∑uv ∈ E 1. So ∑v δ(v) = ∑v∑uv ∈ E 1 = 2|E| since each edge uv is counted both as uv and as vu.
One application of the lemma is that the number of odd-degree vertices in a graph is always even.
106.2. Trees
A tree is an acyclic connected graph. We can show by induction on the number of vertices in G that G is a tree if and only if it is connected and has exactly |V|-1 edges.
We'll start with a lemma that states that G is connected only if it has at least |V|-1 edges. This avoids having to reprove this fact in the main theorem.
- Lemma
- Any connected graph G = (V,E) has |E| ≥ |V|-1.
- Proof
- By induction on |V|. The base cases are |V| = 0 and |V| = 1; in either case we have |E| ≥ 0 ≥ |V|-1.
For a larger graph G = (V,E), suppose that |E| < |V|-1; we will show that in this case G is not connected. From the handshaking lemma we have ∑v∈V δ(v) = 2|E| < 2|V|-2. It follows that there is at least one vertex u with δ(u) ≤ 1. If δ(u) = 0, we are done: G is not connected. If δ(u) = 1, consider the graph G-{u} obtained by removing u and its incident edge. This has |EG-{u}| = |E| - 1 < |VG-{u}| - 1 = |V| - 2; by the induction hypothesis, G-{u} is not connected. But since G-{u} is not connected, neither is G: if v and w are nodes with no path between them in G-{u}, then adding u doesn't help.
Now we can prove the full result:
- Theorem
- Let G be a nonempty connected graph. Then G is acyclic if and only if it has exactly |V|-1 edges.
- Proof
-
We'll prove that a nonempty connected graph with |V|-1 edges is a tree by induction on |V|. The base case is |V| = 1 and |E| = 0; this single-vertex graph is easily seen to be acyclic. For larger |V|, from the Handshaking Lemma we have that ∑ d(v) = 2|E| = 2|V|-2. So from the Pigeonhole Principle there exists a vertex v with d(v) < 2. We can't have d(v) = 0, or G wouldn't be connected, so d(v) = 1. Now consider the graph G-v; it has |V|-1 vertices and |E|-1 = |V|-2 edges, and by the induction hypothesis, it's acyclic. Adding back v can't create any new cycles because any cycle that enters v has no edge to leave on. So G is also acyclic.
Now we need to show that if we have more than |V|-1 edges, some cycle exists. We'll do this by showing that an acyclic connected graph has at most |V|-1 edges, by induction on |V|. For |V| = 1 we have at most |V|-1 = 0 edges whether we are acyclic or not; this gives us the base case for free. Now consider an acyclic connected graph with |V| > 1 vertices. Choosing some vertex v0 and construct a path v1, v2, ... by choosing at each step a node vi+1 that is a neighbor of vi and that is not already in the path. Eventually this process terminates (we only have |V| vertices to work with) with some vertex vk. If vk is adjacent to some vertex vj already in the path, where j≠k-1, then we have a cycle vj...vk. If vk has a neighbor that's not in the path, then we could have added it. So it follows that vk is adjacent only to vk-1 and has degree 1. Delete vk to get G-vk an acyclic graph with |V|-1 vertices and |E|-1 edges. From the induction hypothesis we have |E|-1=|V|-2 implying |E|=|V|-1 for G.
For an alternative proof based on removing edges, see BiggsBook Theorem 15.5. This also gives the useful fact that removing one edge from a tree gives exactly 2 components.
106.3. Spanning trees
Here's another induction proof on graphs. A spanning tree of a nonempty connected graph G is a subgraph of G that includes all vertices and is a tree (i.e. is connected and acyclic).
- Theorem
- Every nonempty connected graph has a spanning tree.
- Proof
- Let G = (V,E) be a nonempty connected graph. We'll show by induction on |E| that G has a spanning tree. The base case is |E| = |V|-1 (the least value for which G can be connected); then G itself is a tree (by the theorem above). For larger |E|, the same theorem gives that G contains a cycle. Let uv be any edge on the cycle, and consider the graph G-uv; this graph is connected (since we can route any path that used to go through uv around the other edges of the cycle) and has fewer edges than G, so by the induction hypothesis there is some spanning tree T of G-uv. But then T also spans G, so we are done.
106.4. Eulerian cycles
Let's prove the vertex degree characterization of graphs with Eulerian cycles. As in the previous proofs, we'll take the approach of looking for something to pull out of the graph to get a smaller case.
- Theorem
- Let G be a connected graph. Then G has an Eulerian cycle if and only if all nodes have even degree.
- Proof
-
(Only if part). Fix some cycle, and orient the edges by the direction that the cycle traverses them. Then in the resulting directed graph we must have δ-(u) = δ+(u) for all u, since every time we enter a vertex we have to leave it again. But then δ(u) = 2δ+(u) is even.
(If part). Suppose now that δ(u) is even for all u. We will construct an Eulerian cycle on all nodes by induction on |E|. The base case is when |E| = 2|V| and G = C|V|. For a larger graph, choose some starting node u1, and construct a path u1u2... by choosing an arbitrary unused edge leaving each ui; this is always possible for ui≠u1 since whenever we reach ui we have always consumed an even number of edges on previous visits plus one to get to it this time, leaving at least one remaining edge to leave on. Since there are only finitely many edges and we can only use each one once, eventually we must get stuck, and this must occur with uk = u1 for some k. Now delete all the edges in u1...uk from G, and consider the connected components of G-(u1...uk). Removing the cycle reduces δ(v) by an even number, so within each such connected component the degree of all vertices is even. It follows from the induction hypothesis that each connected component has an Eulerian cycle. We'll now string these per-component cycles together using our original cycle: while traversing u1...,uk when we encounter some component for the first time, we take a detour around the component's cycle. The resulting merged cycle gives an Eulerian cycle for the entire graph.
Why doesn't this work for Hamiltonian cycles? The problem is that in a Hamiltonian cycle we have too many choices: out of the δ(u) edges incident to u, we will only use two of them. If we pick the wrong two early on, this may prevent us from ever fitting u into a Hamiltonian cycle. So we would need some stronger property of our graph to get Hamiltonicity.
107. BipartiteGraphs
A graph (see GraphTheory) is a bipartite graph if its vertex set can be written as X∪Y and every edge is an element of X×Y. Alternatively, a graph is bipartite if it can be 2-colored (the vertices in the two color sets give X and Y). Yet another criterion is that a graph is bipartite if and only if it does not contain a cycle with an odd number of edges.
108. Bipartite matching
Bipartite graphs are often used to model assignment problems, where the vertices of the left-hand side X represent things that need to be assigned, the vertices of the right-hand side Y represent places to put them, and an edge indicates compatibility. A complete bipartite matching is a subset of the edges of a bipartite graph such that every node is the endpoint of exactly one edge: such a matching corresponds to an assignment that assigns every object and fills every niche (it also implies |X|=|Y|). This is a special case of a matching, which is a subset of the edges of an arbitrary graph that hits each vertex at most once, and a maximal matching, a matching that is maximal under inclusion---i.e., one where you can't add any more edges without making it no longer be a matching.
Because of the application to assignment, much is known about bipartite matching. In particular, there is a characterization of exactly which bipartite graphs have a complete matching.
- Hall's Theorem
- Let G = (X∪Y, E) be a bipartite graph, and for each A⊆X define ∂A = {y∈Y: ∃x∈A such that xy∈E}. Then G has a complete matching if and only if |∂A| ≥ |A| for all A⊆X.
- Proof
If there is some A with |∂A| < |A| we are clearly in trouble, so the main thing is to show that |∂A| ≥ |A| is sufficient. We do so by showing that when the condition holds, any matching M with |M| < |X| can be extended to a matching of size |M|+1. The procedure is as follows: Let x1 be an unmatched node in M and let X1 = {x1}. We will construct two sequences of nodes x1, x2 ..., xk and y1, y2 ..., yk such that yi is matched to xi+1 when i < k, yk is unmatched, and yi is adjacent to at least one node xj with j ≤ i. The construction proceeds as follows: given x1..xi and y1..yi-1 (i = 1 is the special case where we start with just x1 and no y's), we have |∂{x1...xi}| ≥ i > |{y1..yi-1}|. So there is at least one node in ∂{x1...xi} - {y1..yi-1}; pick that node and call it yi. If yi is unmatched, we are done. Otherwise, let xi+1 be yi's match in M and repeat. Now we have that each yi is adjacent to some xj with j ≤ i, and that that xj is either x1 or is matched with yj-1. So working backwards from yk we construct a sequence of nodes yk = y'mx'my'm-1x'm-1...y'1x'1 = x1 where each y'm is adjacent to x'm but not matched to it in M and each y' or x' except yk and x1 is matched in M (such a sequence is called an augmenting path. So by deleting all of the edges in M between some y' and x' and replacing them with edges between y'i and x'i for each i, we remove m-1 edges and add m, increasing the size of the matching by 1.
A useful corollary of Hall's Theorem is that even if there is no complete matching, there is still a matching that matches all but maxA |A|-|∂A| nodes in X. The essential idea is that we can make Hall's condition hold by adding exactly that many new nodes to Y that can be matched with any node in X. The nodes that are matched with the new nodes in the resulting complete matching become the unmatched losers in the original graph.
109. NumberTheory
Contents
Number theory is the study of the natural numbers, particularly their divisibility properties. Throughout this page, when we say number, we mean an element of ℕ.
110. Divisibility and division
A number m divides n, written m|n, if there is some number k such that km=n. In this case m is said to be a factor or divisor of n. A number greater than 1 whose only factors are 1 and itself is called prime. Non-primes that are greater than 1 are called composite. The remaining numbers 0 and 1 are by convention neither prime nor composite; this allows us to avoid writing "except 0 or 1" in a lot of places later.
Some useful facts about divisibility:
- If d|m and d|n, then d|(m+n). Proof: Let m = ad and n = bd, then (m+n) = (a+b)d. ∎
- If d|n and n≠0, then d ≤ n. Proof: n = kd ≠ 0 implies k ≥ 1 implies n = kd ≥ d. ∎
- d|0 for all d. Proof: 0d = 0. ∎
- If p is prime, then p|ab if an only if p|a or p|b. Proof: follows from the extended Euclidean algorithm (see below). ∎
If n is not divisible by m, then any attempt to divide n things into m piles will leave some things left over.
The division algorithm yields for integers (which might or might not be natural numbers) n and m≠0 unique integers q, r such that n = qm+r and 0≤r<|m|. The number q = ⌊n/m⌋ is called the quotient of n divided by m and r = n mod m is called the remainder of n divided by m. The number m is called the divisor or (when we are mostly interested in remainders) the modulus.
The quotient is often written as ⌊n/m⌋, the floor of n/m, to make it clear that we want the integer version of the quotient and not some nasty fraction. The remainder is often written as (n mod m), pronounced "the remainder of n modulo m" when paid by the word but usually just "n mod m." Saying that n mod m = 0 is that same as saying that m divides n.
That a unique quotient and remainder exist can be proved any number of ways, e.g. by induction on |n|, but the easiest is probably this method taken from BiggsBook §8.2. Let's assume for the moment that n and m are both non-negative. Consider the set R = { r | r ≥ 0 and there exists some q such that n = qm+r }. Observe that R is non-empty since it contains n. Since this is a nonempty subset of the naturals, it has a least element—call it r. We already have r ≥ 0 by definition, and if r ≮ m we have r = n - qm implies the existence of r' = n-(q+1)m ≥ 0 with n = (q+1)m + r' and thus r is not the minimum (note we need m≠0 here so that r'≠r). So for the minimum r we have 0 ≤ r < m.
Note that this r is unique (since R only has one minimum), but we haven't proved that it's the only element of R less than m (BiggsBook cheats a bit on this point). To do so, consider any r' with r' ≥ r and corresponding quotient q' such that n = qm+r = q'm+r'. Then r' - r = m(q-q'). If q-q' = 0, r' = r and we are happy. If q-q' ≥ 1, then r' - r ≥ m and thus r' ≥ m + r ≥ m.
So far we have only proved the result when n and m are both non-negative. If m is negative, use the existence and uniqueness of q and r such that n = q(-m)+r with 0 ≤ r < -m to get n = (-q)(m) + r with 0 ≤ r < |m|. If n is negative, first compute -n = q'm + r' and then let either (a) q = -q' and r = 0 if r' = 0 or (b) q = -q'-1 and r = m-r' if r' > 0. In the first case we then have n = qm+r = (-q')m + 0 = -(q'm+r') as expected, and in the second we have n = qm+r = (-q'-1)m + (m-r') = -q'm - m + m - r' = -(q'm+r').
Note that quotients of negative numbers always round down. For example, ⌊(-3)/17⌋ = -1 even though -3 is much closer to 0 than -17. This is so that the remainder is always non-negative (14 in this case).
111. Greatest common divisors
Let m and n be numbers, where at least one of m and n is nonzero, and let k be the largest number for which k|m and k|n. Then k is called the greatest common divisor of m and n, written gcd(m,n) or sometimes just (m,n). A similar concept is the least common multiple lcm(m,n), which is the smallest k such that m|k and n|k. If divisibility is considered as a partial order, the naturals form a lattice (see Relations), which is a partial order in which every pair of elements x and y has both a unique greatest element that is less than or equal to both (the meet x∧y, equal to gcd(x,y) in this case) and a unique smallest element that is greater than or equal to both (the join x∨y, equal to lcm(x,y) in this case). Two numbers m and n whose gcd is 1 are said to be relatively prime or coprime, or simply to have no common factors.
111.1. The Euclidean algorithm for computing gcd(m,n)
Euclid described 23 centuries ago what is now known as the Euclidean_algorithm for computing the gcd of two numbers (his original version was for finding the largest square you could use to tile a given rectangle, but the idea is the same). Euclid's algorithm is based on the recurrence
- gcd(0,n) = n. (This holds because k|0 for all k.)
gcd(m,n) = gcd(n mod m, m), when m > 0. (If k divides both n and m, then k divides n mod m = n - ⌊n/m⌋m; and conversely if k divides m and n mod m, then k divides n = m + ⌊n/m⌋. So (m,n) and (n mod m, m) have the same set of common factors and the greatest of these is the same.)
The algorithm simply takes the remainder of the larger number by the smaller recursively until it gets a zero, and returns whatever number is left.
111.2. The extended Euclidean algorithm
The Extended Euclidean algorithm not only computes gcd(m,n), but also computes integer coefficients m' and n' such that
- m'm + n'n = gcd(m,n).
It has the same structure as the Euclidean algorithm, but keeps track of more information in the recurrence. Specifically:
- For m = 0, gcd(m,n) = n with n' = 1 and m' = 0.
For m > 0, let r = n mod m and use the algorithm recursively to compute a and b such that am + br = gcd(m,r) = gcd(m,n). Substituting r = n - ⌊n/m⌋m gives am + b(n - ⌊n/m⌋m) = gcd(m,n); this can be rewritten as bn + (a-b⌊n/m⌋)m = gcd(m,n), giving both the gcd and the coefficients n' = b and m' = (a-b⌊n/m⌋).
111.2.1. Example
Here's a computation of the gcd of 402 and 176, together with the extra coefficients:
- Finding gcd(402,176)
- Finding gcd(176,50)
- Finding gcd(50,26)
- Finding gcd(26,24)
- Finding gcd(24,2)
- Finding gcd(2,0)
- Base case!
- Returning 1⋅2 + 0⋅0 = 2
- Computing m' = a - b⌊n/m⌋ = 1 - 0⋅12 = 1
- Returning 0⋅24 + 1⋅2 = 2
- Finding gcd(24,2)
- Computing m' = a - b⌊n/m⌋ = 0 - 1⋅1 = -1
- Returning 1⋅26 + -1⋅24 = 2
- Finding gcd(26,24)
- Computing m' = a - b⌊n/m⌋ = 1 - -1⋅1 = 2
- Returning -1⋅50 + 2⋅26 = 2
- Finding gcd(50,26)
- Computing m' = a - b⌊n/m⌋ = -1 - 2⋅3 = -7
- Returning 2⋅176 + -7⋅50 = 2
- Finding gcd(176,50)
- Computing m' = a - b⌊n/m⌋ = 2 - -7⋅2 = 16
- Returning -7⋅402 + 16⋅176 = 2
(Code that generated this: euclid.py.)
111.2.2. Applications
If gcd(n,m) = 1, then there is a number n' such that nn' + mm' = 1. This number n' is called the multiplicative inverse of n mod m and acts much like 1/n in ModularArithmetic.
- If p is prime and p|ab, then either p|a or p|b. Proof: suppose p∤a; since p is prime we have gcd(p,a) = 1. So there exist r and s such that rp+sa=1. Multiply both sides by b to get rpb + sab = b. Observe that p|rpb and p|sab (the latter because p|ab), so p divides their sum and thus p|b. ∎
112. The Fundamental Theorem of Arithmetic
Let n be a number greater than 0. Then there is a unique sequence of primes p1≤p2≤...≤pk such that n = p1p2...pk. This fact is known as the Fundamental Theorem of Arithmetic, and the sequence {pi} is called the prime factorization of n.
Showing that there is at least one such sequence is an easy induction argument. If n=1, take the empty sequence; by convention, the product of the empty sequence is the multiplicative identity, i.e. 1. If n is prime, take p1 = n; otherwise, let n = ab where a and b are both greater than 1. Then n = p1...pkq1...qm where the pi are the prime factors of a and the qi are the prime factors of b. Unfortunately, this simple argument does not guarantee uniqueness of the sequence: it may be that there is some n with two or more distinct prime factorizations.
We can show that the prime factorization is unique by an induction argument that uses the fact that p|ab implies p|a or p|b (which we proved using the extended Euclidean algorithm). If n=1, then any non-empty sequence of primes has a product greater than 1; it follows that the empty sequence is the unique factorization of 1. If n is prime, any factorization other than n alone would show that it isn't; this provides a base case of n=2 and n=3 as well as covering larger values of n that are prime. So suppose that n is composite, and that n = p1...pk = q1...qm, where {pi} and {qi} are nondecreasing sequences of primes. Suppose also (by the induction hypothesis) that any n' < n has a unique prime factorization.
If p1 = q1, then p2...pk = q2...qm and so the two sequences are identical by the induction hypothesis. Alternatively, suppose that p1 < q1; note that this also implies p1 < qi for all i, so that p1 doesn't appear anywhere in the second factorization of n. But then p∤q1...qm = n, a contradiction.
112.1. Applications
Some consequences of unique factorization:
- We can compute gcd(a,b) by factoring both a and b and retaining all the common factors, which is the algorithm favored by grade school teachers who deal with small numbers. Without unique factorization, this wouldn't work: we might get unlucky and factor a or b the wrong way so that the common factors didn't line up. For very large numbers, computing prime factorizations becomes impractical, so Euclid's algorithm is a better choice.
Similarly, for every a, b, there is a least common multiple lcm(a,b) with the property that a|lcm(a,b), b|lcm(a,b), and for any x with a|x and b|x, lcm(a,b)|x. The least common multiple is obtained by taking the maximum of the exponents on each prime that appears in the factorization of a or b. It can also be found by computing lcm(a,b) = ab/gcd(a,b).
The natural numbers without zero, partially ordered by divisibility, form a lattice that is isomorphic to the lattice obtained by taking all infinite sequences of natural numbers whose sum is nonzero and finite, and letting x ≤ y if xi ≤ yi for all i. The isomorphism maps n to x where xi is the exponent in the prime factorization of n on the i-th largest of all primes (e.g. 24 = 23×31 → 3,1,0,0,0,...). If we throw in 0, it becomes a new element at the top of the lattice.
113. Modular arithmetic and residue classes
From the division algorithm, we have that for each n, m there is a unique remainder r with 0≤r<m and n = qm+r for some q; this unique r is written as (n mod m). Define n ≡m n' (read "n is congruent to n' mod m") if (n mod m) = (n' mod m) or equivalently if there is some q ∈ ℤ such that n = n' + qm. Because congruence is a relation defined by pulling equality back through a function, it's an equivalence relation (see Relations), and we can partition the integers into equivalence classes (called residue classes, where residue is an old synonym for remainder) [0]m, [1]m, [2]m, ..., [m-1]m. These equivalence classes ℤ/≡m form the integers mod m, written as ℤm. Usually we will drop the brackets and just write 0, 1, 2, ..., m-1; sometimes a (mod m) will be tacked on the end of any equation we write to remind ourselves that we are working in ℤm.
The most well-known instance of ℤm is ℤ2, the integers mod 2: the class [0]2 is known as the even numbers and the class [1]2 as the odd numbers.
113.1. Arithmetic on residue classes
We can define arithmetic operations on residue classes in ℤm just as we defined arithmetic operations on integers (defined as equivalence classes of pairs of naturals). Given residue classes [x]m and [y]m, define [x]m + [y]m = [x+y]m, where the addition in the RHS is the usual integer addition in ℤ. So, for example, in ℤ2 we have 0+0 = 0, 0+1 = 1, 1+0 = 1, and 1+1 = 0 (since 1+1 = 2 ∈ [0]m). Note that as with the integers, we must verify that this definition of addition is well-defined: in particular, it doesn't matter which representatives x and y we pick.
- Theorem
If x ≡m x' and y ≡m y', then x+y ≡m x'+y'.
- Proof
Choose qx, qx', r, qy, qy' and s such that x = qxm+r, x' = qx'm+r, y = qym+s, and y'=qy'm+s. Then x+x' = (qx+qy)m+(r+s) and y+y'=(qx'+qy')m+(r+s). It follows that (x+y) mod m = (r+s) mod m = (x'+y') mod m and x+y ≡m x'+y' as claimed. ∎
Similarly, we can define -[x]m = [-x]m and [x]m×[y]m = [x×y]m. A similar argument to the proof above shows that these definitions also give well-defined operations on residue classes. All of the usual properties of addition, subtraction, and multiplication are inherited from ℤ: addition and multiplication are commutative and associative, the distributive law applies, etc.
For example, here is an addition table for ℤ3:
+ |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
1 |
1 |
2 |
0 |
2 |
2 |
0 |
1 |
and here is the multiplication table:
× |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
2 |
0 |
2 |
1 |
It may help to think of 2 as -1; so it's not surprising that 2×2 =4 ≡m 1 = -1×-1.
Using these tables, we can do arbitrarily horrible calculations in ℤ3 using the same rules as in ℤ, e.g. 2(1+2)-2 = 2(0)-2 = -2 = 1 (mod 2). Note we tack on the "(mod 2)" at then end so that the reader won't think we've gone nuts.
Comment: the fact that [x]m + [y]m = [x+y]m and [x]m × [y]m = [xy]m for all x and y means that the remainder operation x ↦ x mod m is a homomorphism from ℤ to ℤm: it preserves the operations + and × on ℤ. We'll see more examples of homomorphisms between sets with attached operations (called algebras) in AlgebraicStructures.
113.2. Structure of ℤm for composite m: the Chinese Remainder Theorem
The Chinese Remainder Theorem, in the form typically used today, says that if m1 and m2 are relatively prime (i.e. gcd(m1,m2) = 1), then for each pair of equations n mod m1 = n1, n mod m2 = n2, there is a unique solution n with 0≤n<m1m2. (Chinese Remainder Theorem gives more history of this result.)
Example: let m1 = 3 and m2 = 4. Then the integers m from 0 to 11 can be represented as pairs (m1, m2) as follows:
m |
m1 |
m2 |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
0 |
3 |
4 |
1 |
0 |
5 |
2 |
1 |
6 |
0 |
2 |
7 |
1 |
3 |
8 |
2 |
0 |
9 |
0 |
1 |
10 |
1 |
2 |
11 |
2 |
3 |
Proof: We will prove something stronger and show an isomorphism between ℤm and ℤm1×ℤm2, where ℤm1×ℤm2 is the set of pairs of elements (x,y) with addition defined by (x,y)+(x',y') = (x+x',y+y') and multiplication by (x,y)(x,y')=(xx',yy'). To go from ℤm to ℤm1×ℤm2, define f(n) = (n mod m1, n mod m2). Showing that f is an isomorphism requires showing it preserves addition and multiplication (i.e., that it is a homomorphism: f(a+b) = f(a)+f(b) and f(ab) = f(a)f(b)) and that it is bijective. For addition, observe that if a = kam1+a' and b = kbm1+b', then a+b mod m = a+b - xm for some x, which equals (ka+kb-xm/m1)m1+(a'+b')-xm=km1+(a'+b' mod m) for some k; thus, a+b mod m = (a mod m) + (b mod m) mod m. By symmetry, the same holds if we replace m1 by m2. For multiplication, perform the similar calculation ab mod m = ab - xm for some x, which equals (kam1+a')(kbm1+b')-xm = m1(kakb+kab'+kba'-xm/m1) + a'b' ≡m1 a'b' (and similarly for m2).
Now we must show that f is invertible. Let c1 = m2(m2-1 (mod m1)) and c2 = m1(m1-1 (mod m2)). (The inverses exist because gcd(m1,m2)=1.) These coefficients correspond to the pairs (1,0) and (0,1), because c1 = m2m2-1 = 1 (mod m1) and c1 = 0 (mod m2), and similarly for c1. So given (n1,n2), we can compute n = (n1c1+n2c2) mod m and have n mod m1 = n1*1 + n2*0 = n1 and n mod m2 = n1*0 + n2*1 = n2. We have just shown f is invertible, which implies it is an isomorphism. ∎
113.3. Division in ℤm
One thing we don't get general in ℤm is the ability to divide. This is not terribly surprising, since we don't get to divide (without remainders) in ℤ either. But for some values of x and some values of m we can in fact do division: for these x and m there exists a multiplicative inverse x-1 (mod m) such that xx-1 = 1 (mod m). We can see the winning x's for ℤ9 by looking for ones in the multiplication table below:16
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
2 |
0 |
2 |
4 |
6 |
8 |
1 |
3 |
5 |
7 |
3 |
0 |
3 |
6 |
0 |
3 |
6 |
0 |
3 |
6 |
4 |
0 |
4 |
8 |
3 |
7 |
2 |
6 |
1 |
5 |
5 |
0 |
5 |
1 |
6 |
2 |
7 |
3 |
8 |
4 |
6 |
0 |
6 |
3 |
0 |
6 |
3 |
0 |
6 |
3 |
7 |
0 |
7 |
5 |
3 |
1 |
8 |
6 |
4 |
2 |
8 |
0 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Here we see that 1-1 = 1, as we'd expect, but that we also have 2-1 = 5, 4-1 = 7, 5-1 = 2, 7-1 = 4, and 8-1 = 8. There are no inverses for 0, 3, or 6.
What 1, 2, 4, 5, 7, and 8 have in common is that they are all relatively prime to 9. This is not an accident: when gcd(x,m) = 1 we can use the extended Euclidean algorithm (see NumberTheory) to find x-1 (mod m). Observe that what we want is some x' such that xx' ≡m 1, or equivalently such that x'x + qm = 1. But the extended Euclidean algorithm finds such an x' (and q) whenever 1 = gcd(x,m).
If gcd(x,m) ≠ 1, then x has no multiplicative inverse in ℤm. The reason is that if some d>1 divides both x and m, it continues to divide xx' and m for any x'≠0. So in particular xx' can't be congruent to 1 mod m since qm+1 and m don't share any common factors for any value of q.
The set of of residue classes [x]m where gcd(x,m) = 1 is written as ℤ*m. For a prime p, ℤ*p includes all non-zero elements of ℤp, since gcd(x,p) = 1 for any x that is not 0 or a multiple of p.
113.3.1. The size of ℤ*m and Euler's Theorem
The size of ℤ*m, or equivalently the number of numbers less than m whose gcd with m is 1, is written φ(m) and is called Euler's totient function or just the totient of m. When p is prime, gcd(n,p) = 1 for all n with 0<n<p, so φ(p) = |ℤ*p| = p-1. For a prime power pk, we similarly have gcd(n,pk) = 1 unless p|n. There are exactly pk-1 numbers less than pk that are divisible by p (they are 0, p, 2p, ... (pk-1)p), so φ(pk) = pk - pk-1 = pk-1(p-1). For composite numbers m that are not prime powers, finding the value of φ(m) is more complicated; but we can show using the ChineseRemainderTheorem that in general
![\[
\phi\left(\prod_{i=1}^{k} p_i^{e_i}\right) = \prod_{i=1}^{k} p_i^{e_i-1}(p_i-1).
\] \[
\phi\left(\prod_{i=1}^{k} p_i^{e_i}\right) = \prod_{i=1}^{k} p_i^{e_i-1}(p_i-1).
\]](/pinewiki/NumberTheory?action=AttachFile&do=get&target=latex_591ac29457bafec49b95585d7ea0e31d1c4dc994_p1.png)
One reason φ(m) is important is that it plays a central role in Euler's Theorem, which says that aφ(m) = 1 (mod m) when gcd(a,m) = 1.
We can prove this using an argument adapted from the proof of BiggsBook Theorem 13.3.2: Let z1, z2, ..., zφ(m) be the elements of ℤ*m. For any y ∈ ℤ*m, define yℤ*m = { yz1, yz2, ..., yzφ(m) }. Since y has a multiplicative inverse mod m, the mapping z ↦ yz (mod m) is a bijection, and so yℤ*m = ℤ*m (mod m). It follows that ∏i zi = ∏i yzi = yφ(m) ∏i zi (mod m). But now multiply both sides by (∏i zi)-1 to get 1 = yφ(m) (mod m) as claimed.
For the special case that m is a prime, Euler's Theorem is known as Fermat's Little Theorem, and says ap-1 = 1 (mod p) for all primes p and all a such that p∤a.17
Euler's Theorem is popular in cryptography; for example, the RSA encryption system is based on the fact that (xe)d = x (mod m) when de = 1 (mod φ(m)). Here x is encrypted by raising it to the e-th power mod m, and decrypted by raising the result to the d-th power. It is widely believed that publishing e and m reveals no useful information about d provided e and m are chosen carefully.
113.4. Group structure of ℤm and ℤ*m
Assumes previous knowledge of GroupTheory.
The set of residue classes [x]m where gcd(x,m) = 1 form an abelian group (see GroupTheory).
We will now show that ℤ*m = { x | 0 < x < m, gcd(x,m) } also forms an abelian group, whose operation is multiplication mod m (i.e. x*y = xy mod m), provided m is at least 2.
To show that ℤ*m is an abelian group, we need to show closure, commutativity, associativity, existence of an identity (1), and existence of inverses.
- Closure
Let x and y be in ℤ*m so that gcd(x,m) = 1 and gcd(y,m) = 1. z = xy mod m = xy - km where k = ⌊xy/m⌋. Let p be any prime factor of m. If p|xy, then p|x or p|y; since x and y have no common factors with m, neither does xy. Subtracting km can't create a common factor with m, so gcd(z,m)=1. We also have 0≤z<m (true of all remainders), and z can't equal zero because gcd(0,m)=m≠0.
- Commutativity
- Trivial: xy mod m = yx mod m because xy = yx.
- Associativity
- The only tricky thing here is that taking mods in between multiplications might break associativity. We'll argue though that xyz mod m = (xy mod m) z mod m; by symmetry this will also show xyz mod m = (yz mod m) x mod m = (xy mod m) z mod m. To prove the claim, observe that xy = (xy mod m) + km for some k. Then xyz = (xy mod m) z + kzm, and xyz mod m = (xy mod m) z mod m + (kzm mod m) = (xy mod m) z mod m since kzm mod m = 0.
- Identity
- 1.
- Inverses
Let gcd(x,m) = 1. Then the extended Euclidean algorithm returns x',m' such that x'x+m'm=1. So (x'x + m'm) mod m = 1 mod m or x'x mod m = 1. So let x-1 = x' mod m. We can easily show that x-1 has gcd(x-1,m)=1: if p divides m, then xx-1 = km+1 = kk'p+1 which can't be divisible by p because it has remainder 1 when divided by p. But if p does not divide xx-1, it can't divided either of x or x-1, and so x-1 in particular has no common factors with m.
Note that we could define the additive group ℤm as a quotient group of (ℤ,+) by the congruence x~y if x mod m = y mod m. This almost works for ℤ*m—but the problem is that ℤ with multiplication is not a group, because it doesn't have inverses. The best that we can do is construct the quotient monoid (ℤ,×)/~, which will contain at least one element with no inverse (0), and possibly many others.
114. DivisionAlgorithm
115. ModularArithmetic
116. ChineseRemainderTheorem
117. GroupTheory
A group is an algebra (see AlgebraicStructures) with an associative binary operation (usually written as either multiplication or addition), a constant identity element e such that ex = xe = x for all x, and an inverse operation x -> x-1 such that xx-1 = x-1x = e for all x. If it is also the case that xy=yx for all x and y, the group is abelian. Group theory is the study of the structure of groups.
More formally, a group is a set G together with an operation *:S×S→S that satisfies:
- Closure
- ∀x,y ∈ G, x*y ∈ G. (This is implicit in the fact that *:S×S→S.)
- Associativity
- ∀x,y,z ∈ G, (x*y)*z = x*(y*z)
- Identity
- ∃e∈G ∀x∈G e*x = x*e = x.
- Inverses
∀x∈G ∃x-1∈G x*x-1 = x-1*x = e.
An abelian group also satisfies:
- Commutativity
- ∀x,y∈G xy=yx.
Abelian groups are often written using + for the group operation to emphasize their abelianness, with -x for the inverse of x. So in an abelian group we might write the inverses axiom as ∀x∈G ∃(-x)∈G x+(-x) = (-x)+x = e.
There are also words for algebras that satisfy only some of these axioms: if we take away inverses, we get a monoid; if we take away inverses and the identity, we get a semigroup, and if we take away associativity as well, we get a magma. These structures are discussed in more detail in AlgebraicStructures, but for now we will content ourselves with groups.
118. Some common groups
The symmetric group on n letters, written Sn, has as its elements the n! distinct bijections from an n-element set (often taken to be {1...n}) to itself, with composition as the binary operation.18 Each element of Sn is called a permutation for obvious reasons. For compactness, permutations are often written in cycle notation: this is a sequence of cycles grouped by parentheses, where the interpretation of (x1x2...xk) is that the permutation maps x1 to x2, x2 to x3, and so on, with xn mapping to x1. Cycles that consist of a single element only are omitted. So for example the permutation that shifts each element of S5 up by one would be written (12345) (or (34512) or something---there is no requirement that a particular element appear first in the cycle) and the permutation that swaps 2 with 4 and 1 with 5 while leaving 3 alone would be written as (24)(15). Multiplying permutations consists of tracking the individual elements through the various cycles. So for example, in S5, (24)(15) * (12345) = (14)(23). (To see this, follow each number through the two permutations: 1->2->4, 4->5->1, 2->3->3, 3->4->2, and 5->1->5.) The cyclic decomposition of a permutation is a form of factoring: the permutation is obtained by multiplying the individual cycles together (since they don't move any common elements, the order doesn't matter). See SymmetricGroup.
The free group on a set S consists of all sequences of terms x and x-1 (where x ranges over the elements of S) in which xx-1 and x-1x do not appear.
The cyclic group of order n, isomorphic to ℤn, has elements {p0, p1, ..., pn-1}, with pipj= p(i+j) mod n. Here pk is defined formally for any k∈ℤ as a product of k copies of p (if k is positive), -k copies of p-1 (if k is negative), or the empty product and group identity e (if k is zero). For additive groups, pk is written as kp.
For any m, the set ℤ*m of elements of ℤm that are relatively prime to m forms a group under multiplication. It is isomorphic to ℤp-1 when p is prime.
The symmetry group of a geometric object consists of all ways of rotating and/or flipping the figure so that the resulting figure is congruent to the original. Each such transformation is called a symmetry of the object. Some examples:
The symmetry group of an equilateral triangle is isomorphic to S3 (label the corners 1, 2, 3 and observe that we can move corner one to any position by rotation and then swap the other two as needed by a flip).
The symmetry group of an isosceles triangle is isomorphic to P2 (we can flip the two endpoints of the unequal edge)
- The symmetry group of a general triangle is the trivial group consisting only of the identity (we can't do anything).
The symmetry group Dn of an n-gon (an n-sided polygon) has is called the dihedral group on n points and has 2n elements: to specify a particular symmetry, we pick a particular vertex and say where it goes (n choices) and then say which of its two neighbors ends up on its left or right (2 choices). If a is the operation that rotates the vertices one position clockwise and b is the operation that flips the n-gon about vertex #1, then we have b2=an=e and ab = ba-1. Note that this group is not abelian.
The symmetry group of a (non-square) rectangle is isomorphic to ℤ2×ℤ2, since we can flip it independently either the short way or the long way.
The alternating subgroup An of Sn consists of all permutations that can be carried out by an even number of two-element swaps. (See below for a definition of a subgroup.)
The general linear group GLn(ℝ) (or just GL(n)) of invertible real-valued n×n matrices. The group operation is standard matrix multiplication, inverse in matrix inverse, and the identity element is the identity matrix. Also works if we replace ℝ with any other ring. It's not hard to show that Sn is a subgroup of GLn(R) for any ring (it maps to the permutation matrices, which have exactly one 1 in each row and column), so any finite group can be represented as a subgroup of GL(n) for some n. Some groups have more compact representations: for example, for any m the group ℤm can be represented in GLn(ℂ) by the 1×1 matrices in the set { [ exp(2πin/m) ] | n∈ℤ }, since exp(2πi) = 1. Expressing finite groups as subgroups of GL(n) is a common way to analyze the structure of groups and is the central tool in representation_theory.
119. Arithmetic in groups
Here are some useful facts that apply in any group:
(xy)-1 = y-1x-1. Proof: (xy)(y-1x-1) = x(yy-1)x-1 = (xe)x-1 = xx-1^ = e.
xy = xz ⇒ y = z. Proof: Multiply both sides on the left by x-1 to get x-1xy = x-1xz ⇒ ey = ez ⇒ y = z.
yx = zx ⇒ y = z. Proof: Multiply both sides on the right by x-1 to get yxx-1 = zxx-1 ⇒ y = z.
The functions fx(y) = xy and gx(y) = x are both bijections. Proof: That they are injective is immediate from the previous two facts. That they are surjective follows from f-1(z) = x-1z (as can be verified by computing f(f-1(z)) = xx-1z = z) and g-1(z) = zx-1.
The equations ax = b and xc = d both have unique solutions. Proof: immediate from bijectivitity of fx and gx above.
- The identity e is unique. This follows from the preceding, but I've always liked this proof: Suppose there are e and e' such that ∀x, ex = xe = e'x = xe' = x. Then observe that ee' = e (letting x = e) and ee' = e' (letting x = e'), from which e = e'.
120. Subgroups
A subgroup is a subalgebra of a group. In English, H is a subgroup of G if H is a subset of G that is closed under G's group operation, i.e. such that for all x,y∈H, x*y ∈ H. For example, the even integers are a subgroup of the integers (with addition as the group operation). The statement that H is a subgroup of G is sometimes abbreviated as H < G.
The subgroup of G generated by an element x, written <x>, is the smallest subgroup of G that contains x, where subgroups are ordered by inclusion. The existence of <x> is immediate from the fact that (a) there is at least one subgroup of G that contains x---G itself, and (b) the intersection of any number of subgroups that contain x is itself a subgroup containing x. So we can take the intersection of all the subgroups that contain x and get <x>.
There is a simpler way to write <x>. If we define x0 = e, xn for n > 0 as xxn-1, and x-n for n > 0 as x-1x-(n-1), then <x> is precisely { xn | n ∈ ℤ }, the set of all powers of x. Note that it is possible that this set contains duplicates: for example, in ℤ6, 3+3 = 0 and so <3> consists only of the elements 0 and 3. The size of the subgroup generated by x is equal to the smallest n such that xn = e (if such an n exists); this quantity is called the order or index of x in G. A subgroup generated by a single element is called a cyclic subgroup; we'll talk more about these below.
121. Homomorphisms and isomorphisms
A homomorphism f:G→H is a function from the elements of G to the elements of H such that f(xy) = f(x)f(y) for all x,y in G. For example, the function n↦(n mod m) is a homomorphism from ℤ to ℤm, since taking remainders preserves addition. It is not hard to show that homomorphisms preserve the identity (if f(eG) ≠ eH, we are in trouble when we compute f(xeG) = f(x)f(eG) ≠ f(x)) and inverses (since f(x)f(x-1) = f(eG) = f(x-1)f(x) implies f(x-1) = f(x)-1). A homomorphism that is bijective is called an isomorphism.
122. Cartesian products
Given G and H, the product group G×H has elements of the form (x,y) where x∈G and y∈H and the product rule (x,y)(x',y') = (xx',yy').
Isomorphisms between various products of cyclic groups are discussed in BiggsBook §20.6.
123. How to understand a group
Groups in general can be very complex, and it may be difficult to wrap your mind around an arbitrary group unless you can find some way to break up its structure into brain-sized pieces. Here are four basic strategies that group theorists have come up with for doing this:
By looking at it as a subgroup of Sn, i.e. as a collection of bijections (called actions) on some set. This works for any finite group: we can always take the group itself as the set, and for each group element a the function f:G->G defined by f(x) = xa is a bijection (the inverse is f-1(x) = xa-1). Other examples of groups constructed in this way are the symmetry groups of various figures described above, or the automorphism group of a graph (or any structure that has automorphisms).
By giving a set of generators a, b, c, etc. and relations that describe when various products of the generators and their inverses are equal. An example of this was the description of the dihedral group Dn as being generated by elements a and b (generators) with an = e and ab = ba-1 (relations). Formally, this approach is equivalent to taking a quotient of the free group by a congruence generated by one of its subgroups, as we will describe in more detail below.
- By looking at what subgroups the group has. Even if the original group itself is hard to grasp, it may have simpler structures buried within it.
By expressing the group as a product of simpler groups. This is particularly useful for abelian groups, as all abelian groups are isomorphic to a product of cyclic groups ℤm, where m is a power of a prime.
We will start by looking at how subgroups relate to a group, and in particular how subgroups can sometimes generate congruences that can be used to construct quotient groups.
124. Subgroups, cosets, and quotients
Let G be a group, and let H be a subgroup of G. For each element a of G, define Ha = { xa | x in H }. Such a set is called a right coset. We can similarly define aH = { ax | x in H }, a left coset; everything we say about right cosets will also be true of left cosets, after reversing the group operation throughout.
The right cosets of a subgroup have the same size (sometimes called order by group theorists) as the subgroup itself:
- Lemma 1
- |H| = |Ha| for all a.
- Proof
Let f:H->Ha be the function f(x) = xa. Observe that f has an inverse f-1(y) = ya-1; it follows that f is a bijection.
It is also not hard to show that the cosets partition G:
- Lemma 2
- For any a, b, either Ha = Hb or Ha∩Hb = Ø.
- Proof
Suppose y appears in both Ha and Hb; we will show that any z in Ha is also in Hb. We have y = xa = wb for some x, w in H. It follows that a = x-1wb. Let z = qa where q is in H. Then z = qx-1wb. But q, x, and w are all in H, so qx-1w is as well, and z is in Hb. A symmetric argument shows that any z'∈Hb is also in Ha, so Ha = Hb.
Combining the two lemmas gives:
- Theorem 3
- If H is a subgroup of G, then |H| divides |G|.
This is not true in general for e.g. monoids---the important difference is that the existence of a-1 means that multiplying by a is invertible and creates a bijection. Though one can define right cosets for any subalgebra and binary operation, both the equal-size lemma and the partition lemma depend on the existence of inverses.
An immediate consequence of the Theorem is that any group whose size is a prime (e.g. ℤp) has no nontrivial19 proper20 subgroups.
124.1. Normal subgroups
Partitioning all elements of G into right cosets of a subgroup H creates an equivalence relation: a is right congruent to b, written a ≡r b (mod H), if Ha = Hb, or equivalently if ab-1 is in H. For non-abelian groups, right congruence is not in general a congruence in the algebraic sense. We can see this by observing that if it were a congruence, then then we could construct a quotient group G/≡r in which H (as the equivalence class containing e) acted as the identity. But since the identity commutes, we would need aH = Ha for all a. Though this equation is true for many subgroups, it is not true for all.
A subgroup H of G for which aH = Ha for all a is called a normal subgroup. If H is a normal subgroup of, we write H ⊲ G. Any subgroup of an abelian group is normal. A group is called simple if it has no normal subgroups; an example is the dihedral group Dn. This group has a subgroup of order n (the rotations that don't flip) and many subgroups of order 2 (the flips around particular vertices), but none of them are normal.
Given a subset S of G, the intersection of all normal subgroups of G that are supersets of S is a also normal subgroup, called the normal subgroup generated by S. In general the normal subgroup generated by S will be larger than the subgroup generated by S.
If N is a normal subgroup of G, then ≡r (mod N) is a congruence: (Ha)(Hb) = HaHb = HHab = Hab. We write G/H for the quotient group obtained from G and this congruence. Group theorists have historically approached the understanding of groups by trying to dividing them into quotients over subgroups, ultimately leading to towers of simple groups that cannot be divided further. This doesn't entirely identify the group: for example, the distinct groups ℤ4 and ℤ2×ℤ2 both have ℤ2 as a normal subgroup and in both cases ℤ4/ℤ2 = ℤ2×ℤ2/ℤ2 = ℤ2, but it gives some information.
The problem of identifying the simple groups, at which this process stops, is known as the problem of classification of finite simple groups and was a major outstanding problem in group theory from the mid-19th century until its final completion in 1985.
124.2. Cyclic subgroups
Let G be a group and let a be an element of G. Then the set <a> = { ak | k in ℤ } is a subgroup of G, called the cyclic subgroup generated by a. (Proof that it's a subgroup: <a> contains the identity e = a0, and for any ai and aj in <a>, aiaj = ai+j is in <a>.) This is an easy way to generate subgroups of a group; for example, the non-normal subgroups of the dihedral group consisting of all non-flipping rotations or particular non-rotating flips are just the cyclic groups generated by particular operations.
Some other examples of cyclic subgroups of a group:
In ℤ, the subgroup <2> generated by 2 consists of all the even integers. This is often written as 2ℤ. Every subgroup of ℤ turns out to be of this form: it is dℤ where d is the greatest common divisor of the elements in the group.
ℤ itself is a cyclic subgroup of Q or R, the additive groups of the rationals or reals, generated by 1 in each case.
The index of an element a is the least positive integer k for which ak = e, or 0 if there is no such integer (this only happens in infinite groups: the proof is that in a finite group, as we generate the sequence a0, a1, a2, ... we must eventually get ai = aj for some i, j; but then a|i-j| = e). When the index is nonzero, it is also the size of <a>, as any element am where m is less than 0 or greater than or equal to k will be equal to some element in the set { a0, a1, ..., ak-1 }. It follows from the theorem in the previous section that the index of any element of a finite group (if nonzero) divides the order of the group that contains it.
For permutations, the index can be calculated directly from the cyclic decomposition; it's the least common multiple of the cycle lengths. A well-known application of this is the answer to the problem "how many perfect shuffles does it take to restore a 52-card deck of playing cards to its original state?" Here we define a "perfect shuffle" as a permutation that interleaves the top and bottom halves of the deck, which (if we number the cards from 0 to 51) sends card 0 to position 0, 26 to position 1, 1 to position 2, 27 to position 3, and so on, ultimately leaving card 51 in place. Formally, we can think of this as the function f(x) = 2x mod 51 for x < 51, and we want to know how many iterations of f are needed to get the identity.
If we try writing down the cyclic decomposition of f, we get (0)(1 2 4 8 16 32 13 26)(3 6 12 24 48 45 39 27)(5 10 20 40 29 7 14 28)(9 18 36 21 42 33 15 30)(11 22 44 37 23 46 41 31)(17 34)(19 38 25 50 49 47 43 35)(51). This is the product of many 8-element cycles, one 2-element cycle, and two 1-element cycles; so the LCM is 8 and 8 perfect shuffles equals the identity. (A quicker way to see this is to observe that f(k)(x) = 2k x mod 51 when x < 51, and 28 mod 51 = 256 mod 51 = 1.)
124.3. Finding the subgroups of a group
Given a group, how do we find subgroups? For finite groups, it's often enough to pick a few elements and ask "what subgroup is generated by these elements?" The more difficult problem is knowing when you've gotten all the subgroups. Here facts like Theorem 3 (|H| divides |G| when H is a subgroup of G) can be handy for excluding possibilities we might have missed.
For example, let's find all the subgroups of Dp where p is a prime. The order of Dp is 2p, and the only subgroup orders we are interested in that divide 2p are 2 and p, so any nontrivial proper subgroup either has size 2 (i.e., it consists of the identity and one other element that is its own inverse) or p. It's not hard to see where we can get size 2 subgroups (any flip generates one) and a size p subgroup (all the rotations). But are these all the subgroups?
First observe that the subgroup of non-flipping rotations is generated by any nontrivial rotation. The proof is that any such rotation is of the form x=ak for some k (where a is our rotate-one-position-to-the-right generator), and if the index of x is some m < p we have akm = e which implies km is a multiple of p. But then km contains a factor of p and p is not prime.
It follows that as soon as we have a single rotation, we have all the rotations. So we can't get any more subgroups using just rotations.
Can we get another subgroup using, say, two flips? Suppose we flip around 1 and then around some other position c. Then after both flips 1 is moved to position 2c-1 and the polygon is not flipped---in other words, the product of these two flips is a nontrivial rotation. So we have a subgroup that contains a nontrivial rotation, which means that it contains all p rotations, and it also contains at least two flips. This means the subgroup has at least p+2 elements; but the only number greater than or equal to p+2 that divides 2p is 2p itself. So as soon as we have two flips (or a rotation and a flip), we have the entire group.
We have just shown that the nontrivial proper subgroups of Dp consist precisely of (a) p 2-element subgroups generated by flips around particular vertices of the polygon, and (b) one p-element subgroup containing all rotations. Note that we used the fact that p was prime; for general Dn we might get more subgroups.
125. Homomorphisms, kernels, and the First Isomorphism Theorem
Let f:G→H be a homomorphism. Define the kernel of f as the set Ker(f) = f-1(eH) = { x∈G | f(x) = eH }.
It is easy to show that the kernel is always a normal subgroup of G. To show that it is a subgroup, first observe that if x, y are in Ker(f), then f(xy) = f(x)f(y) = eHeH = eH implies xy is also in Ker(f). Similarly if f(x) = eH then f(x-1) = eH-1 = eH and thus Ker(f) is closed under inverses. To show that Ker(f) is normal, we need to show that for any a, the coset a Ker(f) = Ker(f) a. We can do so by observing that for any b in Ker(f), f(ab) = f(a)f(b) = f(a), and similarly f(ba) = f(b)f(a) = f(a). So a Ker(f) = Ker(f) a = f-1(f(a)), or equivalently a' is in a Ker(f) = Ker(f) a precisely when f(a') = f(a). This latter equation defines the kernel relation of f, which does not depend on G being a group and has useful properties for more general algebraic structures; but for groups it is enough to track the kernel as a subgroup.
It is also the case that the image of f, defined as Im(f) = { y∈H | y = f(x) for some x∈G } is a subgroup of H. The proof is that if y and y' are both in Im(f), then y=f(x) and y'=f(y') for some x, x' in G, and so yy' = f(x)f(x') = f(xx') ∈ Im(f). (For a surjective homomorphism, Im(f) = H, but not all homomorphisms are surjective.) The image of f is not necessarily normal; for example, the image of f:ℤ2→S3 given by f(0) = () and f(1) = (1 2) is a subgroup { (), (1 2) } of S3, but this subgroup is not normal.
We can use the fact that the image of a homomorphism is a subgroup to rule out certain homomorphisms between groups. For example, if there is an injective homomorphism f from ℤm to ℤn, then Im(f) is a subgroup of ℤn of size m, and we must have m|n.
Because the kernel is normal, we can take a quotient G/Ker(f). The First Isomorphism Theorem says that G/Ker(f) is always isomorphic to Im(f). This is a special case of an even more general theorem for arbitrary algebras, but for groups we can prove it quickly. Observe first that the elements of G/Ker(f) are precisely the inverse images of elements of Im(f), i.e. the sets f-1(y) = { x∈G | f(x) = y } for each y in Im(f). We will show that this map f-1 from elements if Im(f) to elements of G/Ker(f) is the desired isomorphism. Given two elements f-1(y) and f-1(y') of G/Ker(f), their product is obtained by taking representatives x and x', multiplying them, and taking the equivalence class that contains them. But then we have f(xx') = f(x)f(x') = yy' and so f-1(y)f-1(y') = f-1(yy'). By a similar argument, we have (f-1(y))-1 = f-1(y-1), and so f-1 is a homomorphism. But it is also an isomorphism: it's surjective (easy) and injective (since f is a function) and thus a bijection.
For example, the homomorphism f from Sn to ℤ2 based on whether a permutation is the product of an even or odd number of transpositions (see SymmetricGroup) has as its kernel the alternating group An of even permutations, and the quotient group Sn/An consists of the set of even permutations and the set of odd permutations and is isomorphic to ℤ2.
On the other hand, we can use the First Isomorphism Theorem to rule out the existence of certain homomorphisms. For example, there is no nontrivial homomorphism21 from Sn to ℤp when p > n, since ℤp has no nontrivial proper subgroups, and if f were a surjective homomorphism from Sn to ℤp, we'd have a subgroup Ker(f) of Sn such that |Sn| = n! would be a multiple of |Sn/Ker(f)| = p, but n isn't big enough for this to happen. Or for a homomorphism f from ℤm to ℤn, we can show that |Im(f)| divides both n (because Im(f) is a subgroup of ℤn) and m (because Im(f) ≈ ℤm/Ker(f) implies that |Im(f)| = |ℤm|/|Ker(f)| divides m); it follows that any such homomorphism has |Im(f)| ≤ gcd(m, n).
126. Generators and relations
One way to define a group is to specific a set of generators, and to give relations between them. Such groups are written as (S|R) where S is the set of generators and R is the set of relations. In principle any group can be defined in this way: we let the set of generators be all the elements of the group, and let the relations be all equations of the form xy=z that are true in the group. In practice this approach is only useful when a group is generated by a small number of generators and relations, as with ℤ = (a|), ℤm = (1|m1 = 0), Dn = (a,b|an=e,b=b-1,ab=ba-1), or ℤ2×ℤ2 = (a,b|a2=e,b2=e,ab=ba). The notation can be further simplified by converting each relation to the form w=e where w is some word and dropping the "=e" part; this gives ℤ = (a|), ℤm = (1|m1), Dn = (a,b|an,b2,abab), and ℤ2×ℤ2 = (a,b|a2,b2,aba-1b-1) for the examples. A definition of a group in this form is called a presentation of the group.
The intuition behind a presentation is that the resulting group is just big enough to contain all the generators and everything that can be generated from them, but not so big that the relations stop being true. This intuition should remind you of free algebras, and in fact the formal definition of (S|R) takes a quotient of the free group F(S) on S:
- Definition
- Let S be a set of elements and R a set of words (i.e., elements of F(S)) over S. Then (S|R) = F(S)/N, where N is the normal subgroup of F(S) generated by the elements of R.
As before, the normal subgroup generated by R is just the intersection of all normal subgroups of F(S) that contains R. This will consist in particular of all words of the form r0s1r1s2r2...skrk where each ri is the product of elements of R and their inverses and s1...sk = e in F(S).
Note that the same group may have multiple presentations; the S part will be the same, but different sets of relations might generate the same subgroup of F(S).
One consequence of the definition of (S|R) is that (S|R) inherits some of the properties of the free group. In particular, any homomorphism from G=(S|R) to some group H is completely determined by where it sends the generators:
- Theorem 4
Let G=(S|R) and let f:G->H and g:G->H be homomorphisms. Then if f(x)=g(x) for all x in S, f(x)=g(x) for all x in G.
- Proof
Because G is a quotient group of F(S), there exists a homomorphism h:F(S)->G with h(x) = x for all x in S. Now consider the homomorphisms (f∘h) and (g∘h) from F(S) to H. If x is in S, we have (f∘h)(x) = f(x) = g(x) = (g∘h)(x). Using the definition of a free algebra, there is a unique homomorphism that maps each x in S to f(x) = g(x), so we have (f∘h) = (g∘h). Now take some y in G, and let z be such that h(z) = y. Then f(y) = f(h(z)) = g(h(z)) = g(y).
127. Decomposition of abelian groups
Finite abelian groups have a particularly simple structure:
- Theorem (Kronecker Decomposition Theorem)
Let G be a finitely abelian group of size n > 1. Then G is isomorphic to a product of cyclic groups of prime power order, i.e. there are prime numbers p1, p2, ... pm and positive integers k1, k2, ... km such that
![\[G \approx \prod_{i=1}^{m} {\mathbf Z}_{p_i^{k_i}}.\] \[G \approx \prod_{i=1}^{m} {\mathbf Z}_{p_i^{k_i}}.\]](/pinewiki/GroupTheory?action=AttachFile&do=get&target=latex_59c4ca3fc97b7fef75c82c4356c448dfd428d21b_p1.png)
Note that the product of the sizes of the groups in the product must equal the size of the product group. This allows us to quickly identify all the isomorphism classes of abelian groups of a given size. For example, there is one (up to isomorphism) 6-element group, isomorphic to ℤ2×ℤ3, because 2×3 is the only way to factor 6 into prime powers. In contrast, there are two 4-element groups: ℤ2×ℤ2 and ℤ4; and five 16-element groups: ℤ2×ℤ2×ℤ2×ℤ2, ℤ2×ℤ2×ℤ4, ℤ2×ℤ8, ℤ4×ℤ4, and ℤ16.
The proof of the Theorem was hard enough to get Kronecker's name attached to it, so we will not attempt it here.
128. SymmetricGroup
The symmetric group on n letters, written Sn, has as its elements the n! distinct bijections from an n-element set (often taken to be {1...n}) to itself, with composition as the binary operation.18 Each element of Sn is called a permutation for obvious reasons.
129. Why it's a group
To be a group, Sn requires closure (trivial), associativity (follows from associativity of function composition), an identity (the identity permutation 1→1, 2→2, ..., n→n) and inverses (follows from the fact that any bijection has an inverse). So Sn is a group.
130. Cycle notation
For compactness, permutations are often written in cycle notation: this is a sequence of cycles grouped by parentheses, where the interpretation of (x1x2...xk) is that the permutation maps x1 to x2, x2 to x3, and so on, with xn mapping to x1. Cycles that consist of a single element only are omitted. So for example the permutation that shifts each element of S5 up by one would be written (12345) (or (34512) or something---there is no requirement that a particular element appear first in the cycle) and the permutation that swaps 2 with 4 and 1 with 5 while leaving 3 alone would be written as (24)(15).
To obtain the cycle notation for a permutation, pick any element of the set and follow its orbit---the elements it is sent to by applying the permutation over and over again---until you get back to the original element. This gives one of the cycles of the permutation. For example, in the permutation { 1→2, 2→4, 3→5, 4→1, 5→3 } the orbit of 1 is 1, 2, 4, 1, ... and the corresponding cycle would be written as (124). We always get a cycle that returns to the first element because (a) the set is finite, so we must eventually repeat an element in the orbit, and (b) if we don't return to the initial element, i.e. we get an orbit of the form x0x1...xi-1xi...xjxi where xi is the first repeated element, then the alleged permutation isn't injective, a contradiction. Continuing with our example, there is a second cycle starting a 3 consisting of 3 and 5, so the whole permutation could be written as (124)(35).
Multiplying permutations consists of tracking the individual elements through the various cycles. So for example, in S5, (24)(15) * (12345) = (14)(23). To see this, follow each number through the two permutations: 1->2->4, 4->5->1, 2->3->3, 3->4->2, and 5->1->5. The cyclic decomposition of a permutation is a form of factoring: the permutation is obtained by multiplying the individual cycles together. Note that since the cycles in the cycle decomposition don't move any common elements, the order doesn't matter: in general this is not true.
131. The role of the symmetric group
The reason the symmetric groups are important is that they embed all other finite groups. Specifically, we have
- Theorem
Let G be a group with n elements. Then G is isomorphic to a subgroup of Sn.
- Proof
Let a1, a2, ..., an be the elements of G. For each a in G define a function fa:G→G by fa(b) = ab. Each such fa is a bijection (fa^-1^ is it inverse), and the set of such functions is closed under composition (since fa(fb(c)) = abc = fab(c)); thus it's a subgroup of the group of all bijections from the elements of G to the elements of G, which is isomorphic to Sn (relabel a1...an,, as 1...n).
For example, the cyclic group ℤm is isomorphic to the subgroup of Sm generated by (1 2 3 ... m). Many symmetry groups can easily be shown to be isomorphic to subgroups of Sn for some n by labeling the vertices of the geometrical figure and describing group operations in terms of how they permute these vertices.
(See BiggsBook §21.5 for more on this.)
132. Permutation types, conjugacy classes, and automorphisms
An automorphism of a group is an isomorphism between the group and itself. Automorphisms of Sn are obtained by conjugating by some group element σ; this is the operation that sends τ to στσ-1. Intuitively, conjugation corresponds to relabeling the elements being permuted: σ-1 undoes the relabeling, τ permutes the original elements, and σ restores the relabeling. It is easy to see that conjugation by σ is an isomorphism: its inverse is conjugation by σ-1 (since σ-1(στσ-1)σ = τ) and it preserves multiplication: (στσ-1)(σρσ-1)=στ(σ-1σ)ρσ-1=σ(τρ)σ-1.
Conjugation can be used to define an equivalence relation on permutations: two permutations τ and ρ are conjugate if there is some σ such that ρ = στσ-1. The simplest way to detect if two permutations are conjugate is to look at their cycle decompositions: τ and ρ are conjugate if and only if they have the same number of cycles of each length (see BiggsBook Theorem 12.5). The number of cycles of each length is summarized as the type of a permutation, which is writen as a sequence of cycle lengths, possibly with counts as exponents, in brackets. For example, the permutation (124)(35) on S5 has type [23], while the permutation (12)(34) has type [1 22] (the 1 is for the omitted (5) cycle of length 1). It's not at all clear what this is useful for, but BiggsBook makes a big deal about it in §12.5.
133. Odd and even permutations
There is a homomorphism from Sn to ℤ2 that classifies all permutations as odd (those mapped to 1) or even (those mapped to 0). The essential idea is that a permutation is odd or even depending on whether the number of cycles in its cycle decomposition (including the length-1 cycles that we usually don't bother to write down) is odd or even, except that for odd n the correspondence is reversed, as otherwise the identity permutation (with an odd number of cycles) wouldn't map to the identity element 0 of ℤ2. The surprising fact is that oddness and evenness adds as in ℤ2 when permutations are multiplied. The oddness or evenness of a permutation σ is often encoded as -1 for odd and 1 for even, and is called the sign of the permutation, written sgn(σ) and equal to (-1)k(-1)n where k is the number of cycles and n is the size of the underlying set. The reason for this encoding is that we can map multiplication of permutations directly to multiplication of integers: sgn(στ) = sgn(σ)sgn(τ). This avoids dealing with ℤ2 directly, which was a popular dodge back in the early days of group theory when this notation was invented.
Note that we still haven't proved that sgn is indeed a homomorphism. The easiest way to do this is to reduce all permutations to products of a smaller basis of odd permutations, and show that if σ = τ1τ2...τk where each τi is in the basis, then sgn(σ) = ∏i sgn(τi). The basis we will use consists of all transpositions, permutations of type [1n-22], or alternatively permutations that exchange two elements with each other while leaving the others untouched. Since each transposition consists of exactly n-1 cycles, it has sign (-1)n-1(-1)n = -1. If we can show that sgn(σ) = ∏i sgn(τi), we get an alternate (and more standard) definition of sgn(σ) as the parity number of transpositions needed to generate σ, which we can then use to argue that sgn(στ) = sgn(σ)sgn(τ) since we can express στ as just the product of the two sequences of transpositions that generate σ and τ.
First we must show that any permutation σ can be written as a product of transpositions. There are a couple of ways to prove this. A computer programmer will probably swap the correct value to position 1, then the correct value to position 2, and so on. This works, but it is not quite as clean a proof as the observation that any cycle (x1 x2 ... xk) = (x1 xk) (x1 xk-1) (x1 xk-2) ... (x1 x3) (x1 x2), in which each xi for i < k is first swapped into position x1 and then back into position xi+1 (remember that permutations are applied right to left). Since any permutation is a product of cycles, and each cycle can be represented as a product of transpositions, we get that any permutation is a product of transpositions.
Now, we can do transpositions all afternoon, and after a while we won't be generating any more permutations. So in general the same permutation may arise as the product of different sequences of transpositions---and even sequences of different length. But what we will show is that the number of transpositions in each sequence generating σ is always odd or even depending on the sign of σ. The proof of this is to show that while a transposition may have unpredictable effects on the number of cycles in σ, it always increases or decreases this number by exactly 1. So the parity of the number of cycles in the product of an even number of transpositions is always the same, and since σ has a unique cycle decomposition (up to reordering the cycles), the number of cycles in the decomposition determines whether there are an even or an odd number of transpositions in any decomposition into transpositions.
- Lemma 1
(x y)(a1 ... ak x b1 ... bm y) = (a1 ... ak y) (b1 ... bm x).
- Proof
Walk the elements through both cycles on the LHS. Each ai except ak is still sent to ai+1, since ai+1 is not affected by (x y). The element ak is sent first to x and then y. The element y is sent to a1 by the right-hand cycle and then is unaffected by (x y). This gives us our first cycle on the RHS. A similar argument shows that (b1 ... bm x) forms the second cycle.
- Corollary 2
(x y)(a1 ... ak y) (b1 ... bm x) = (a1 ... ak x b1 ... bm y)
- Proof
Multiply both sides of the equation in the lemma by (x y); since (x y)2 = e this gives the equation in the corollary (after swapping the LHS with the RHS).
So now we have:
- Lemma 3
- If σ is a permutation with k cycles and τ a transposition, then τσ has either k-1 or k+1 cycles.
- Proof
- Either τ swaps two elements of the same cycle in σ, Lemma 1 applies, and τσ has k+1 cycles, or τ swaps two elements of different cycles, Corollary 2 applies, and τσ has k-1 cycles.
which gives:
- Corollary 4
- If σ is a permutation and τ a transposition, then sgn(τσ) = sgn(τ)sgn(σ) = -sgn(σ).
- Proof
(-1)(k-1) = (-1)k+1 = -(-(-1)k).
and finally:
- Theorem
- For any permutations σ and ρ, sgn(σρ) = sgn(σ)sgn(ρ).
- Proof
- Rewrite σ as a product of transpositions, and then apply Corollary 4 once for each transposition in the expansion of σ.
One consequence of the classification into odd and even permutations is that the even permutations form a subgroup of Sn, called the alternating subgroup An: the inverse of an even permutation is even (expand it into transpositions and then invert the product) and the product of two even permutations is even. The size of An is exactly n!/2, or half the size of Sn. We can prove this by observing that multiplication by any transposition τ gives a bijection between the even permutations and the odd permutations, an observation that is a special case of the proof of Lagrange's Theorem (see GroupTheory or BiggsBook §20.8).
134. AlgebraicStructures
Contents
135. What algebras are
An algebra is a set S (called the carrier) together with zero or more operations, each of which is a function from Sk→S for some k. The value k is the number of arguments to the operation, and is called the arity of the operation. Most operations that one encounters are either unary (one argument) or binary (two arguments); examples are negation (unary) and addition (binary). Some programming languages provide ternary operation with three arguments, like C's notorious ?: operation. Some algebras also include 0-ary operations: most people call these constants. The collection of operations provided by an algebra is called the algebra's signature.
For example, the integers with addition and negation have as carrier the set ℤ and signature (+, 0, -), where + is a binary operation, 0 is a 0-ary operation (i.e., constant), and - is a unary operation. Other operations (e.g. binary -) can be defined using operations in the signature.
Often we use the same letter to refer to both an algebra and its carrier when this will not cause confusion.
136. Why we care
The various standard algebras are abstractions that allow us to reason about lots of different situations at the same time. From the perspective of computer science, they are like base classes high up in an object-oriented type hierarchy, that provide minimal features common to all the classes that inherit from them without specifying the details. So for example in a monoid, where the single operation is associative and there is an identity e that satisfies the equations ae = a and ea = a, we can prove that there can't be a second identity e', since if ae' = a for all a we have ee' = e (from ea = a) and ee' = e' (from ae' = a), giving e = e'. This tells use that we can't extend ℤ by adding a second copy of 0 or the set of n×n matrices by adding a second copy of I; but we didn't need to know anything specific about either structure to know this.
Similarly we can sometimes recognize that our proofs (or later, our algorithms) don't require the detailed structure of ℚ, or ℝ, or ℤ, but in fact work in any algebra of the appropriate type. For example, in computing the length of a path through a graph, we take the sum of the edge weights, and in computing the shortest path, we take the min over all such paths. If we know a lot about semirings, we might recognize this as a sum over products in the (min,+) semiring, and realize that many of our shortest-path algorithms might work equally well in any other semiring.
137. Cheat sheet: axioms for algebras (and some not-quite algebras)
Axioms |
Name |
Anything that satisfies this and above is a |
0 binary operations |
||
|
|
set |
1 binary operation + |
||
|
|
magma |
x+(y+z)=(x+y)+z |
Associativity |
semigroup |
0+x=x+0=x |
Identity |
monoid |
x+(-x)=(-x)+x=0 |
Inverse |
group |
x+y=y+x |
Commutativity |
abelian group |
2 binary operations + and ⋅ |
||
x(y+z)=xy+xz, (y+z)x=yx+yz |
Distributivity |
|
x(yz)=(xy)z |
Associativity (multiplicative) |
rng (ring without the multiplicative identity)22 |
1x=x1=x |
Identity (multiplicative) |
ring |
xy=yx |
Commutativity (multiplicative) |
commutative ring |
xx-1=x-1x=1 when x≠0 |
Inverse (multiplicative) |
field |
Semirings don't quite fit into this progression; they act like rings, but the + operation gives a commutative monoid instead of an abelian group. An example is the (max,+) semiring, where max acts as the addition operator and + (which distributes over max) acts as multiplication.
See below for examples.
138. Classification of algebras with a single binary operation (with perhaps some other operations sneaking in later)
The simplest interesting algebras consist of a set together with a single binary operation (*, say). These algebras are classified depending on what axioms * satisfies. Each of the classes below adds an additional constraint to the previous one.
138.1. Magmas
If * satisfies closure (which just says that its codomain is S), then (S,*) is a magma (or sometimes groupoid, but groupoid is more often used to mean something else that is more useful: see Groupoid). There really isn't very much to say about magmas, but we can define one interesting magma: the free magma on a set A has as its elements (1) all the elements of A, and (2) (x*y) for any x and y in the magma. This effectively generates all binary trees whose leaves are elements of A.
138.2. Semigroups
A magma (S,*) becomes a semigroup if its operator is associative, that is, if (x*y)*z = x*(y*z) for all x, y, and z in S. Semigroups show up quite often in ComputerScience. Examples are:
- Let A be a set, and S be a set of functions from A to A. Then (S,∘) is a semigroup, where ∘ is the composition operation defined by (f∘g)(x) = f(g(x)).
Let A+ be the set of nonempty finite sequences of elements of some alphabet A. Then (A+,+) is a semigroup, where + is the concatenation operation: abc+def = abcdef. This semigroup is called the free semigroup on A.
Let ℤ+ be the positive integers. Then (ℤ+,+) is a semigroup, which is isomorphic (see below) to (A+,+) if A has only one element.
The empty set Ø and the empty function from Ø2→Ø together make the empty semigroup.
- Let S be a set and let x be an element of S. Define for each y, z in S y*z = x. Then (S,*) is a semigroup.
Most magmas are not semigroups and can't easily be turned into semigroups without destroying information.
138.3. Monoids
A semigroup (S,*) is a monoid if it has an identity element e, that is, if there is an element e such that e*x = x and x*e = x for all x. In algebraic terms, we usually think of the identity element as being provided by a 0-ary operation, also known as a constant.
If there is an identity element, it is easy to prove that it is unique: Let e and e' be identities. Then e*e' = e' (by the e*x=x rule) and e*e' = e (by the x*e'=e' rule). Thus e=e'.
- The semigroup (S,∘) from the previous section is a monoid if S contains the identity function f (for which f(x)=x for all x).
Let A* be the set of all finite sequences of elements of some alphabet A. Then (A*,+) is a monoid (the free monoid on A), whose identity is the empty string <>.
(ℕ,+) and (ℕ,*), where + and * are the usual addition and multiplication operations, are both monoids. Note that (ℤ+,+) is not a monoid, because it doesn't contain the required identity element 0.
- Let A be a set and let S be the power set of A. Then (S,∪) and (S,∩) are both monoids (with identity elements Ø and A, respectively).
- Let S = { x } and let x*x=x. Then (S,*) is a monoid.
- Any semigroup can be turned into a monoid by adding a new identity element (if it doesn't have one already).
138.4. Groups
A monoid (S,*) is a group if for each a and b in S, there are solutions x and y to the equations ax=b and ya=b. This fact is equivalent to the existence of a unary inverse operation taking x to x-1 (or -x when the binary operation is written as +), where x-1x=xx-1=e. The existence of an inverse operation can be derived from the more fundamental definition by proving a sequence of properties of groups that are interesting in their own right:
- Let y∈S. If there exists any x∈S such that xy=x or yx=x, then y=e. (In other words, any y that ever acts like the identity is the identity; this is not true in general in monoids.) Proof: Suppose xy=x; the other case is symmetric. We will show that y = ey = e. Let q be a solution to qx=e. Then y = ey = (qx)y = q(xy) = qx = e.
If xy = e, then yx = e. (This says that if y is a right inverse of x, it is also a left inverse.) Proof: Let xy = e, and observe that yxy = ye = y. Now let q be a solution to yq=e. Then (yxy)q = yq, but (yxy)q = (yx)(yq) = yx and yq = e, so we have yx = e.
- If xy = e and xy' = e, then y = y'. (I.e., right inverses are unique.) Proof: Consider yxy'. Grouping the operations as y(xy') we get yxy' = y(xy') = ye = y. Grouping them the other way gives yxy' = (yx)y' = ey' = y'. So we have y = y'.
It follows that if xy=e, then yx=e and y is uniquely defined by x. Thus the inverse operation x-1 is well-defined (it identifies a unique element of S satisfying the required property xx-1 = x-1x = e). The inverse of the identity is always the identity, since e-1 = e-1e = e.
Note that if we start with an inverse operation, we can easily solve ax=b or ya=b by computing a = axx-1 = bx-1 or a = y-1ya = y-1b.
Examples of groups:
ℤ, ℚ, and ℝ are all groups with the binary operation +, but not with the binary operation * (0 has no inverse). ℚ-{0} and ℝ-{0} (sometimes written ℚ* and ℝ* in this context) are groups with respect to *; ℤ-{0} with multiplication is still not a group (only 1 and -1 have inverses). This is a special case of a general method for extracting a group from a monoid (see below).
Let ℤm be the quotient set of the equivalence relation a~b if a=b (mod m), and define an addition operation on ℤm by the rule <a> + <b> = <a+b>. Then ℤm is a group, called the integers mod m.
Let ℤ*m be the elements of ℤm whose representatives are relatively prime to m. Then (ℤ*m,*) is a group.
Let A be a set, and let S be the set of all bijections from A to A. Then (S,∘) is a group, called the permutation group on A.
Let A be a set of symbols, and let S consist of all finite sequences s in which each position has the value x for some x in A, or x-1 for some x in A, and neither x,x-1 nor x-1,x appear consecutively in s. Define a group operation by concatenation followed by the removal of consecutive xx-1 and x-1x pairs. The resulting algebra is a group, called the free group on A.
Let S = {x} and let x*x=x. Then (S,*) is a group, with identity x and x-1=x.
The set of n×m matrices over ℝ (in general, over any field—see below for the definition of a field) is a group under addition. The set of invertible n×n matrices is a group under multiplication. If we don't require invertibility, we only get a monoid.
Given any monoid M, the set M* of invertible elements of M is a group, where an element x is invertible if there exists some element x-1 such that xx-1 = x-1x = e. Examples include ℚ* = ℚ - { 0 }, ℝ* = ℝ - { 0 }, and, for each n, the group of invertible n×n matrices. A less interesting example is ℤ* = { -1, 1 }. The proof that the invertible elements form a group depends on the fact that if a and b are both invertible, so is ab, since ab(b-1a-1) = (b-1a-1)ab = e. This doesn't work in general in semigroups, because without associativity we can't necessarily regroup ab(b-1a-1) = a(bb-1)a-1 = (ae)a-1 = aa-1 = e. Note that we didn't need to use anything in the proof that ab has an inverse beside the group axioms; so this is an example of the sort of very general proof that can be done by using powerful enough abstractions.
Groups are about the weakest algebraic structure that allow calculations similar to what we expect with ordinary arithmetic: we can add and subtract, solve for unknown variables, etc. Note that the operation in a group does not have to be commutative: it may be that xy ≠ yx for some x and y. For example, in the permutation group on three elements, the function that swaps the first two elements and the function that swaps the last two elements do not commute: 123 → 213 → 231 does not give the same result as 123 → 132 → 312. Similarly, matrix multiplication is in general not commutative.
138.5. Abelian groups
If a group is commutative, which means that xy=yx for all x and y, then it is an abelian group (after Niels Henrik Abel, a 19th-century Norwegian mathematician---but by convention spelled with a lowercase "a" despite its etymology).
All of the groups listed previously except the permutation group (on three or more elements) and the free group are abelian. By convention, the binary operation in an abelian group is often (but not always) written as +.
For more on the structure of groups and abelian groups, see GroupTheory.
139. Operations on algebras
Like sets or graphs, we can define operations that connect one algebra to another or allow us to construct new algebras. When considering multiple algebras, we generally assume that all share the same set of operations (or at least operations with the same names and arities). Most operations on an algebra are defined in terms of operations on the carrier (the set of elements of the algebra).
139.1. Subalgebras
A subalgebra of an algebra A is obtained by taking a subset S' of the carrier that is closed under all operations of the algebra; i.e. for any n-ary operation f, f(x1, ..., xn) is in S' if all the xi are. If B is a subalgebra of A, we write B⊆A, as with subsets.
For specific classes of algebras (such as semigroups, monoids, groups, or abelian groups), any axioms satisfied by the parent algebra are inherited by its subalgebras: e.g., if xy = yx in A, then xy = yx in B⊆A.
One important way to get a subalgebra is the subalgebra generated by a particular element or set of elements. This is the smallest subalgebra of a given algebra that includes the specified elements (which are called generators); formally, this is defined by taking the intersection of all subalgebras that contain the generators. (The proof that taking the intersection of subalgebras gives a subalgebra is left as an exercise.)
Examples:
- Let A and B be sets, which we can think of as algebras with no operations. The B is a subalgebra of A iff B is a subset of A.
Let A be the semigroup (ℕ,+), and let B = { x | x > 137 and x = 3k for some k in ℕ }. Then B is a subsemigroup of A.
Let A be the monoid (ℤ,*), and let B be the monoid (ℤ+,*). Then B is a submonoid of A. Note that 1 has to be present in B for it to be a submonoid, or else B is not closed under the (0-ary) identity operation.
- Let A be the group (ℤ,+), and let S' be the set of all even integers. Then B = (S',+) is a subgroup of A.
- Let A be the group (ℤ,+), and let B be the subalgebra of A generated by 2. Then B is precisely the subgroup described in the previous example.
- Let A be the free monoid over { a, b, c }, and let B be the subalgebra generated by aaa. Then B consists of all strings of k a's where k is a non-negative multiple of 3.
139.2. Homomorphisms
A function from the carrier of A to the carrier of B is a homomorphism, written f:A→B, if for any n-ary operation g, g(f(x1), ..., f(xn)) = f(g(x1, ..., xn)). Note that the g on the left-hand side is B's version of g and the g on the right-hand side is A's. If this equation holds for a particular operation g, f is said to preserve g. A homomorphism preserves all operations.
Examples:
- Any function f:A→B on sets is a homomorphism, since it preserves all none of the operations on sets.
- The composition g∘f of two homomorphisms f:A→B and g:B→C is a homomorphism from A to C.
- Let A be the free magma over a set S and let B be the free semigroup over the same set S. Define f:A→B by f(x) = x whenever x is in S, and f(xy) = f(x)f(y) otherwise. Then f is a homomorphism (immediately from the definition). The effect of f is to "flatten" trees into an ordered list of their leaves.
Let A be the free semigroup over S and let f(x) = 1 for x in S and f(xy) = f(x)+f(y) otherwise. Then f is a homomorphism from A to (ℤ+,+).
Consider the function ℤ → ℤm defined by f(x) = x mod m. Then f is a homomorphism from the additive group of the integers (ℤ, +, 0, -) to ℤm.
- Consider the function f:ℤ→ℤ defined by f(x)=cx for some constant c. Then f(x+y) = c(x+y) = cx + cy = f(x) + f(y), f(0) = c*0 = 0, and f(-x) = c*(-x) = -(cx) = -f(x): f is a group homomorphism from ℤ to ℤ.
In the last case the image of f, defined as f(A) = { f(x) | x in A }, is a subgroup of the codomain ℤ. This turns out always to be the case for images of algebra homomorphisms:
- Theorem 1
- Let f:A→B be an algebra homomorphism. Then f(A) is a subalgebra of B.
- Proof
To show that f(A) = { f(x) | x in A } is a subalgebra of B, we need to show that it is closed under every operation of B. Let g be an n-ary operation of B, and consider g(y1, ..., yn) where each yi is in f(A). Because each yi is in f(A), there exists some xi such that yi = f(xi). So we can rewrite g(y1, ..., yn) as g(f(x1), ..., f(xn,)) = f(g(x1, ..., xn)) ∈ f(A). (The equality holds because f is a homomorphism.)
As with graphs, homomorphisms on algebras give rise to isomorphisms (bijective homomorphisms, the inverses of which will also be homomorphisms) and automorphisms (isomorphisms between an algebra and itself). Every algebra has at least one automorphism, the identity homomorphism that maps every element to itself. An injective homomorphism is called an embedding (sometimes imbedding); any embedding f of A into B gives an isomorphism between A and B's subalgebra f(A).
More examples:
Recall that the free magma on S consists of all binary trees with leaves in S. Let's call this free magma T (for tree). Consider the magma of nonempty LISP lists with atoms in S and the cons operation, defined by x cons (y1 ... yk) = (x y1 ... yk); we'll call this one L (for LISP). Define f:T→L by the rule f(s) = (s) when s∈S and f(T1T2) = f(T1) cons f(T2). Then f is clearly a homomorphism. But we can show that it is in fact and isomorphism, by defining f-1((x)) = x (for length-1 lists) and f-1((x y1 ... yk)) = f-1(x)f-1((y1 ... yk)) (for length-2 and longer lists). It's not hard to verify that that f-1(f(t)) = t for any tree t. If we allow empty binary trees and empty lists, we similarly get an isomorphism between two slightly larger magmas.
Let A be the free monoid on a single-element set S, and define f(an) = n. Then f is a monoid isomorphism between A and (ℕ,+); its inverse is f-1(n) = an. Conversely, if M is a free monoid and g(n) = an for any element a of M, then g is an embedding of (ℕ,+) into M.
Let f:ℕ→ℕ be defined by f(n) = 3n. Then f is a monoid embedding of (ℕ,+) into (ℕ,*), since (a) f is a homomorphism: f(a+b) = 3a+b = 3a3b = f(a)f(b) and f(0) = 30 = 1; and (b) f is injective. It's not an isomorphism because it doesn't have an inverse.
Let f:ℝ→ℝ+ be defined by f(x) = 3x, where ℝ+ = { x∈ℝ | x > 0 }. Now f is an isomorphism between the groups (ℝ,+) and (ℝ+,*). Proof: f(a+b) = 3a+b = 3a3b = f(a)f(b), f(0) = 30 = 1, f(-a) = 3-a = (3a)-1 = f(a)-1, and log3(3x) = x shows that log3 gives an inverse for f.
139.3. Free algebras
We've seen examples of various kinds of algebras that have been called "free", such as free magmas, free semigroups, etc. There is in fact a single definition of a free algebra (from a particular class of algebras) that produces each of these specific free algebras.
The essential idea of a free algebra A over a set S is that (a) it contains all the elements of S, (b) it contains g(x1, ..., xn) for any n-ary operation g whenever x1,...,xn are in A (which is just the closure requirement), and (c) for particular xi and x'i, g(x1,....,xn) = g(x'1,...,xn) only if required by the axioms.
So in a free magma, x(yz) is never equal to (xy)z, no matter what values x, y, and z have. In a free semigroup, x(yz) = (xy)z, always, because of the associativity axiom, but xy is never equal to x for any x and y, xy is never equal to yx, etc. In a free monoid, xe = ex = x, but xy is never equal to x unless y = e, and so forth.
The formal definition that yields these properties is this:
Let C be a class of algebras, where the names and arities of the operations are the same for all algebras in the class, and let S be a set. Then a free algebra in C over S, written F(S) or FC(S), is an algebra in C such that (a) S is a subset of the carrier of F(S), and (b) for any algebra B in C, and any function from S to the carrier of B, there is a unique homomorphism f* from F(S) to B such that f*(x) = f(x) for any x in S. (In this case f is said to lift to f*; another way of expressing this is that f is a subset of f* when both are viewed as sets of ordered pairs.)
How does this definition yield all the specific cases of free algebras? Let's take free monoids as an example. Recall that a free monoid F(S) over S consists of all finite sequences of elements of S, with + = concatenation and 0 = the empty sequence. It's trivially the case that S is a subset of the carrier of F(S) (assuming we identify single elements with one-element sequences). Now let's show that any function f from S to the carrier of some semigroup B lifts to a unique f* from F(S) to S.
Define f*(x1...xk) = f(x1)f(x2)...f(xk). It is easy to see that f* is a (monoid) homomorphism, and that f*(x) = f(x) when x is in S. Now let g be any other monoid homomorphism from F(S) to B such that g(x) = f(x) for any x in S. We'll show that for sequence s=x1...xk in F(S), g(s) = f*(s), by induction on the length k of s. The cases k=0 and k=1 are the base cases. For k=0, g(<>) = f*(<>) = the identity of B because both g and f* are monoid homomorphisms (and therefore must preserve the identity). For k=1, we have g(x1) = f(x1) = f*(x1) by the requirement that g(x) = f(x) when x in S. For k > 1, we have g(x1...xk-1xk) = g(x1...xk-1)g(xk) = f*(x1...xk-1)f*(xk) = f*(x1...xk-1xk).
Note that there may be more than one way to define a free algebra. For example, we could define the free monoid over S by setting + to be reverse concatenation: xyz+abc = abcxyz. This again gives sequences of elements of S, but to translate them back to the previous definition we have to reverse the sequences. Fortunately this reversal operation is an isomorphism between the two monoids, and in general we can show that any free algebra for a given class with a given base set is unique up to isomorphism, which means that while there may be more than one such algebra, there is only one isomorphism equivalence class.
- Theorem 2
- If F and G are free algebras over S in a class C, then F and G are isomorphic.
- Proof
The proof is by repeated application of the uniqueness of f*:F(S)→A for any f:S→A.
Let f:S→G be defined by f(x)=x. Then there is a unique homomorphism f*:F→G.
Similarly, let g:S→F be defined by g(x) = x. Then there is a unique homomorphism g*:G→F.
We will now show that g*=(f*)-1. Consider the homomorphism h=g*∘f*. For any x in S, we have h(x) = g*(f*(x)) = g(f(x)) = x. So h is a homomorphism from F to F, such that for any x in S, h(x)=x. Since F is a free algebra, h is unique among all such homomorphisms: if somebody shows up with another homomorphism h':F→F with h'(x) = x for all x in S, then h'=h. Now out of the box let us pull IF:F→F, the identity homomorphism on F defined by IF(x)=x for all x in F. Clearly IF(x)=x for all x in S, so IF=h. It follows that g*∘f* is the identity---i.e., that g* = (f*)-1. Since f* is invertible and thus bijective, it's an isomorphism, and F and G are isomorphic.
The nice thing about this proof is that at no time did we have to talk about specific operations of the algebras; everything follows from the definition of a free algebra in terms of homomorphisms.
139.3.1. Applications of free algebras
The selling point for free algebras is that we can define homomorphisms just by defining what happens to elements of the underlying set S. This operation is done all the time. Some examples:
Simple Roman numerals (without the IV = V-I rule). Define f(I) = 1, f(V) = 5, f(X) = 10, etc., and assert f is a homomorphism from the free semigroup on {I,V,X,...,M} to (ℤ+,+).
Flattening trees (homomorphism from the free magma to the free semigroup mapping each element of S to itself), counting the number of leaves in a tree (homomorphism from the free magma on S to (ℤ+,+) mapping each element of S to 1), or counting the total weight of the leaves of a tree (homomorphism from the free magma on S to (ℝ,+) mapping each element of S to its weight). Indeed, just about any recursive function on binary trees is an example of a magma homomorphism.
139.4. Product algebras
Let F and G be algebras with the same signatures. Then F×G is an algebra whose elements consist of a pair of one element from F and one from G (i.e., is the usual cartesian product F×G), and an operation f on (F×G)k carries out the corresponding F and G operations on both sides of the ordered pairs.
Examples:
- Consider the monoids F=(ℤ,+,0) and G=(ℤ,*,1). Then elements of F×G are pairs of integers, and the binary operation (which we'll call *) adds the first elements of each pair and multiples the second: (2,3)*(-6,7) = (-4,21). The algebra F×G is a monoid with identity (0,1), which is itself the product of the identities of F and G.
139.5. Congruences and quotient algebras
A congruence is an equivalence relation on elements of an algebra that respects the structure of the algebra. In particular, a relation ~ is a congruence on A if
- It is an equivalence relation on elements of A, and
for any n-ary operation g of A, if x1 ~ y1, x2 ~ y2, ..., xn ~ yn, then g(x1, x2, ... xn) ~ g(y1, y2, ... yn).
An example of a congruence is the relation x~y if x and y are both even or x and y are both odd, where x and y are elements of additive group of the integers (ℤ,+,0,-).
Given a congruence ~ on an algebra A, we can define a quotient algebra A/~ whose elements are the equivalence classes C of ~, and whose operations are defined by letting g(C1...Cn) be the equivalence class of g(x1...xn) where each xi is some element of the corresponding Ci. The requirements for ~ to be a congruence guarantee that this defines a unique equivalence class no matter which representatives xi we pick.
For example, the odd-even congruence defined previously yields a quotient group ℤ/~ = ℤ2, the integers mod 2. Associated with this congruence is a homomorphism that maps each integer to one of the two elements 0 or 1 of ℤ2, depending on whether it is even (0) or odd (1). This is not surprising; in fact, there is always such a homomorphism from any algebra to any of its quotient algebras.
- Theorem 3
- If ~ is a congruence on A, then the function f mapping each x in A to its equivalence class in A/~ is a homomorphism.
- Proof
We need to show that g(f(x1)...f(xn)) = f(g(x1...gn)) for each n-ary operation g and sequence of arguments {xi}. For each i let Ci = f(xi) be the equivalence class of i under ~; by the definition of operations in A/~ we have g(C1...Cn) is the equivalence class of g(x1...gn) = f(g(x1...gn)).
The preceding theorem tells us we can map A onto A/~ via a homomorphism. There is a sense in which we can go the other way: given any homomorphism f:A→B, we can define a congruence ~ on A by x~y if f(x)=f(y). This congruence is called the kernel of f. (Note: in GroupTheory, the kernel is defined differently, as the subgroup Ker f of A given by f-1(e). The relation between the kernel-as-subgroup and the kernel-as-congruence is that in a group we can define a congruence a~b iff ab-1 is in Ker f, which turns out to be equivalent to the definition f(a)=f(b) for algebras in general.)
- Theorem 4
- Let f:A→B be a homomorphism, and let ~ be the kernel of f. Then ~ is a congruence.
- Proof
It is easy to see that ~ is an equivalence relation, so we will concentrate on showing that xi~yi implies g(x1...xn)~g(y1...yn) for any {xi}, {yi}, and g. Pick some particular xi, yi, and g; then we have f(xi)=f(yi) (from the definition of the kernel) and so f(g(x1...xn))=g(f(x1)...f(xn))=g(f(y1)...f(yn))=f(g(y1)...g(yn)), which implies g(x1...xn)~g(y1)...g(yn).
We have previously observed that the image of a homomorphism is a subalgebra of its codomain. This subalgebra turns out to be isomorphic to the quotient algebra of the domain by the kernel of the homomorphism:
- Theorem 5 (First Isomorphism Theorem)
- Let f:A→B be a homomorphism, and let ~ be the kernel of f. Then A/~ is isomorphic to f(A).
- Proof
Define h:(A/~)→B by setting h(C) = f(x), where x is any element of C. Note that h is well-defined because each C consists precisely of all x for which f(x) is some particular element y of B. We can also define an inverse h-1 by letting h-1(y) = { x | f(x) = y }, so h is a bijection. It remains only to show that it is a homomorphism. Let g be an n-ary operation of A/~, and let x1...xn be representatives of equivalence classes C1...Cn. Then h(g(C1...Cn)) = f(g(x1...xn)) = g(f(x1)...f(xn)) = g(h(C1)...h(Cn).
In the case that f is surjective, the theorem gives an isomorphism between A/~ and B. This is a fundamental tool in many branches of algebra.
140. Algebraic structures with more binary operations
All of the structures we have considered so far had only a single binary operation, which we usually wrote as either multiplication or addition. We now consider structures that have more binary operations. The simplest of these, rings and fields, are the natural generalization of the ways that real numbers, integers, etc. support both an addition and a multiplication operation.
140.1. Rings
A ring is a set S together with two binary operations, + and ×, called addition and multiplication (as elsewhere, they are called this because of the symbol used, even if they really do something else). Considering each of the operations separately, we require:
That (S,+) is an abelian group. In particular, there is an additive identity (usually written 0) such that x+0=0+x=x for all x in S, and for each x in S, there is an additive inverse -x such that x + -x = 0.
That (S,×) is a monoid. The multiplication operation is associative, and there is a multiplicative identity (usually written 1) such that x×1=1×x=x for all x in S.
In addition, a distributive law relates the two operations. For all x, y, and z, we have:
- x×(y+z) = (x×y)+(x×z) and (y+z)×x = (y×x)+(z×x).
Note the need for both equations since multiplication is not necessarily commutative.
In writing about rings, we adopt the usual convention that multiplication binds more tightly that addition and drop the multiplication operator, so that we can w, for example, yx+zx for (y×x)+(z×x).
140.1.1. Examples of rings
The integers with the usual addition and multiplication operations. These form a commutative ring, in which multiplication is commutative.
- The integers mod m, with addition and multiplication mod m
The dyadic numbers---rational numbers like 27/1, 53/2, or 91/128 where the denominator is a power of two.
- The rationals.
- The reals.
The ring of polynomials in some variable x with coefficients in some commutative ring R, which is written R[x]. Addition is the usual polynomial addition, e.g. (x+3) + (x2+12) = (x2+x+12), and multiplication is the usual polynomial multiplication, e.g. (x+3) × (x2+12) = (x3+3x2+12x+36). See Polynomials.
Square matrices of fixed size with coefficients in some field. We'll see more of these in AbstractLinearAlgebra, but for the moment let us just observe that they are an example of a non-commutative ring.
Formal power series of the form ∑i aixi, as used in the theory of GeneratingFunctions, where addition and multiplication are as defined there. These differ from ordinary polynomials in that ordinary polynomials can only have a finite number of terms.
140.1.2. Properties of rings
Though rings vary widely in their properties, some properties follow from the definition and thus hold in all rings. Two important theorems about rings are that multiplying by 0 has the effect we expect from our experience with the integers, rationals, etc., and that negation commutes with multiplication.
- Theorem
- Let R be a ring and let x be any element of R. Then 0×x=x×0=0.
- Proof
- We'll prove that 0×x=0; the other case is symmetric. The proof uses both the distributive law and the existence of 1, the multiplicative identity. Compute 0x+x = 0x+1x = (0+1)x = 1x = x = 0+x. But since addition in a ring is a group, if 0x+x = 0+x then 0x = 0.
The familiar rule that (-x)y = -(xy), (-x)(-y) = xy, etc. follows immediately from the preceding theorem:
- Corollary
- Let R be a ring and x and y any elements of R. Then (-x)y = x(-y) = -(xy).
- Proof
- Again we will prove only the first case (-x)y = -(xy). It is enough for this to show that (-x)y + xy = 0. Compute (-x)y + xy = (-x + x)y = 0y = 0. Here the first step uses the distributive law, the second uses the definition of the additive inverse, and the last uses the theorem---just proved---that 0x = 0 for all x.
140.1.3. Invertible elements and zero divisors
An element of a ring is invertible if it has a multiplicative inverse. The element 1 is always invertible, since 1*1=1, and so is -1 (although -1 may be the same element as 1, as in ℤ2). The set of invertible elements is closed under multiplication: if a is invertible and b is invertible, then so is ab (its inverse is b-1a-1). Since it also contains the multiplicative identity and inverses, it's a group, called the multiplicative group of the ring. So the multiplicative groups ℤ*m of integers relatively prime to m are just a special case of this definition.
One way to show that an element is not invertible is to show that it's a zero divisor. An element x is a zero divisor if it divides 0, i.e. if there is some element y≠0 such that xy = 0 or yx=0. For example, in ℤ6, the element 2 is a zero divisor (2*3=0). A zero divisor can't be invertible because if xy=0 and x-1 existed, then y=x-1xy=x-10=0. However, in many rings there are elements that are not invertible without being zero divisors, e.g. 2 in ℤ or x in ℤ[x].
140.1.4. Subrings
A subring S of a ring R is just a subset of R that is also a ring. The main thing we need to prove in order to show that this is true is that S is closed under all the ring operations.
Examples:
- ℤ is a subring of ℚ, which is a subring of ℝ, which is a subring of ℂ. Proof: 0 and 1 are in all of them; a+b is an integer if a and b are both integers, a rational if a and b are both rationals (proof: m/n + m'/n' = (mn'+nm')/(nn')), and a real if and and b are both reals; ab is similarly an integer/rational/real if a and b both are.
- The even integers (more generally, any set of the form mℤ = { mn | n∈ℤ }) is a subring of ℤ.
- The dyadics are a subring of ℚ.
- For any set of primes P, the set ℚ - { m/n | (m,n) = 1 and p|n for some p∈P } is a subring of ℚ. Proof: It contains 0 and 1; and given m/n and m'/n', if p divides nn' in either their sum (mn'+m'n)/(nn') or their product (mm')/(nn') then p divides one of n or n', so it's closed under addition and multiplication.
140.1.5. Ideals and quotient rings
An ideal of a ring R is a subring S such that whenever x is in S, xy and yx are in S for any y in R. An example is the even integers, which are an ideal of the ring of integers. An example of a subring that is not and ideal is the dyadics; (1/2)(1/3) = (1/6), which is not a dyadic.
The main reason for looking at ideals is that they have the same role in rings that normal subgroups have in groups: the additive cosets in R of an ideal I yield a quotient ring R/I. This follows from the fact that as an additive subgroup, an ideal is always a normal subgroup (since addition is commutative), so (I+a)+(I+b)=I+(a+b) is well-defined; and that when we multiply (I+a)(I+b), we get II + Ib + aI + ab = I + ab since the first three terms all collapse into I. One way to remember the required properties of an ideal is that the ideal must act like 0 in the quotient ring it yields: it's an additive identity (normal subgroup) but a multiplicative annihilator (drags products into itself).
Some examples of quotient rings:
ℤ/mℤ is isomorphic to ℤm.
ℚ/ℤ, the rationals mod 1, is obtained from the rationals by keeping only the fractional part after each operation. For example, in ℚ/ℤ, 3/5 + 4/7 = (21+20)/35 = 41/35 = 1 + 6/35 = 6/35.
- ℤ₂[x]/(1+x+x²) as given below in the construction of a finite field of order 4. This is shorthand for ℤ₂[x]/(1+x+x²)ℤ₂[x], where the ideal is the set of all multiples of the polynomial (1+x+x²); the second ℤ₂[x] disappears because of the usual notational laziness.
140.1.6. Ring homomorphisms
A ring homomorphism is a function that preserves all the ring operations (this is just a special case of the usual definition of an algebra homomorphism). So in particular, given a function f:R→S, we need f(0R) = 0S, f(1R) = 1S, f(a+b) = f(a)+f(b), and f(ab) = f(a)f(b). These are pretty strong requirements, so ring homomorphisms are much rarer than, say, group homomorphisms.
Some examples of ring homomorphisms:
If R/S is a quotient ring, there is a homomorphism from R to R/S (this is true for all quotient algebras). So for example, the map f(x) = x mod m is a homomorphism from ℤ to ℤm ≈ ℤ/mℤ.
There is a homomorphism from ℚ - { m/n | (m,n) = 1 and p|n } to ℤp, given by f(m/n) = (m mod p)(n mod p)-1 when m/n is expressed in lowest terms. The tricky part here is showing that addition and multiplication are preserved. For convenience, it may help to show that reducing to lowest terms is only needed to get rid of extraneous copies of p; if a∤p, then (am mod p)(an mod p)-1 = ama-1n-1 = mn-1 = f(am/an) [with all computations in ℤp]. So f(m/n+m'/n') = f((mn'+nm')/nn') = (mn'+nm')(nn')-1 = mn'n-1(n')-1 + nm'n-1(n')-1 = mn-1 + m'(n')-1 = f(m/n) + f(m'/n') and f((m/n)(m'/n')) = f(mm'/nn') = mm'n-1(n')-1 = (mn-1)(m'(n')-1) = f(m/n)f(m'/n'), as desired.
140.2. Semirings
A semiring is like a ring, except that the addition group is replaced by a commutative monoid; alternatively, we can think of a semiring as a ring without additive inverses. The theorem in rings that 0*x=x*0=0 becomes an additional axiom (the annihilation axiom) for semirings—without inverses it is impossible to prove it from the other axioms.
An example of a semiring is the tropical semiring or max-plus semiring on ℝ∪{-∞} where addition is max, multiplication is +, the additive identity is -∞, and the multiplicative identity is 0. This gives a commutative monoid for both addition (max) and multiplication (+), since max and + both commute and max(x,-∞) = x, but neither operation yields a group (for the multiplication operation +, -∞ has no inverse). It also satisfies the distributive law: x+max(y,z) = max(x,y) + max(x,z); and the annihilation axiom: -∞ + x = -∞. The tropical semiring is useful for studying scheduling problems: for example, if it takes 2 years to graduate after taking CPSC 202 and 3 more years after taking MATH 112, then my graudation time is at least max(t202 + 2, t112 + 3), and the ability to manipulate complicated expressions involving max and + may help me plan out more difficult tasks.
For more examples of semirings see Semiring.
140.3. Fields
If the nonzero elements of a commutative ring form an abelian group, the ring is a field. An equivalent definition is that 1≠0 (so the group is nonempty) and every nonzero element is invertible. The most common examples in ordinary mathematics are ℚ, ℝ, and ℂ, with ℤp showing up in NumberTheory. A more exotic example is the field of rational functions F(x1,...xn,): functions of the form p/q where p and q are both polynomials with variables x1 through xn and coefficients in F, with q≠0.
For ComputerScience, the most useful fields are the finite fields, since (being finite) they fit inside computers. There is a unique (up to isomorphism) finite field of size pk for every prime p and every positive integer k. These fields are known as the Galois fields after Evariste_Galois (the guy who died from staying up all night doing his homework) and are written as GF(pk). When k=1, they have a particularly simple construction; for larger values of k the Galois fields are more complicated.
The field GF(p) is just ℤp with multiplication defined mod p. We've already seen (in NumberTheory) that every nonzero element of ℤp has a multiplicative inverse; everything else follows from ℤp being a ring.
For n > 0, there is a standard construction of GF(pn) based on polynomials. The idea is to start with all polynomials over ℤp, and then take remainders mod some particular polynomial to get rid of any high-degree terms. We'll do GF(22) as an example.
Step 1: Consider all polynomials in ℤ2[x]: 0, 1, x, 1+x, 1+x+x3, etc. Note that the only coefficients are 0 and 1, since those are the only elements we have in ℤ2.
Step 2: Choose an irreducible polynomial r, one for which the equation r(x) = 0 has no solutions in ℤ2. The degree (highest exponent) of this polynomial will determine the n in GF(pn). We'll pick r(x) = 1+x+x2. It is easy to check that r(0) = 1+0+0 = 1 and r(1) = 1+1+1 = 1, so it's irreducible.
Step 3: Let the elements of GF(pn) be the residue classes mod r, i.e. the equivalence classes of polynomials where p1~p2 if there is some polynomial q such that p1 = p2 + qr. In GF(22) this means that whenever we multiply two polynomials together and get a polynomial with an x2 in it, we subtract r to get rid of the x2. In this way we take as representatives of the classes the polynomials that have degree at most n-1; in GF(22) this will be the four polynomials 0, 1, x, and 1+x.
Addition of elements of GF(22) is done term by term, e.g. (1+x) + (x) = 1. (The x's cancel since 1+1=0 in ℤ2). Multiplication is more complicated. Here's the full multiplication table:
|
0 |
1 |
x |
1+x |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
x |
1+x |
x |
0 |
x |
1+x |
1 |
1+x |
0 |
1+x |
1 |
x |
Most of the entries in the table are straightforward (we know, for example, that 0*y = 0 for all y). The tricky ones are in the bottom right corner. Let's look at x*x first. This is x2, which is too big, so we'll take the remainder mod x2+x+1, which in this case means computing x2-(x2+x+1)=x+1 (remember we are in ℤ2 where 0-1=1). Similarly we can compute (1+x)*(1+x) = 1 + 2x + x2 = 1+x2 = 1+x2-(1+x+x2) = x. For x(1+x) we have x(1+x) = x+x2 = x+x2-(1+x+x2) = 1.
This construction is a special case of a more general technique called field extension, where one makes an existing field (ℤ2 in this case) bigger by tacking on an extra member (x) that satisfies some polynomial equation not satisfied by any element of the old field (1+x+x2=0). Another example of the same technique is the construction of the complex numbers from the reals by taking ℝ and adding a new element i that satisfies 1+i2=0. Our operation of replacing x2 with x+1 in GF(22) is the equivalent in that field of replacing i2 with -1 in the complex numbers. The fact that we can get away with this in each case can be justified formally by sufficient handwaving about free rings and quotients.
Note that the structure of GF(22) is very different from ℤ4, which isn't a field (since 2*2 = 0 mod 4). Even the additive group of GF(22) is not the same as ℤ4; there is no single element, for example, that generates the entire additive group. This is typical of GF(pn), whose additive group in general will look like the product of n copies of ℤp, and whose multiplicative group will be terribly tangled up.
For more on finite fields see http://mathworld.wolfram.com/FiniteField.html or Chapter 23 of BiggsBook.
- Exercise
- Which of the examples of rings given previously are also fields?
140.3.1. Subfields and homomorphisms
Subfields are fairly common. For example, ℚ is a subfield of ℝ which is in turn a subfield of ℂ. Among finite fields, GF(p) is a subfield of GF(pn) for any n (consider the set of polynomials with only a constant term).
Field homomorphisms are much less common; indeed, we can prove that all homomorphisms between fields are injective (giving an embedding—a bijection between the domain and some subfield of the codomain). Proof: Let f:X→Y be a field homomorphism and suppose that f is not injective; i.e., that f(x)=f(y) for some x≠y. Then f(x-y) = f(x)-f(y) = 0. But since x≠y, x-y has an inverse (x-y)-1, and so f(1) = f((x-y)(x-y)-1) = f(x-y)f((x-y)-1) = 0⋅f((x-y)-1) = 0 ≠ 1, contradicting the requirement that f maps 1 to 1. It follows that any homomorphic f is injective.
140.4. Vector spaces
A vector space is not, strictly speaking, an algebraic structure of the sort we have defined previously, as it involves two classes of objects: scalars, which are elements of some field, and vectors, which are elements of some abelian group, written additively. In addition to their own field and group operations, scalars and vectors are connected by an operation called (rather confusingly) scalar multiplication that multiplies a scalar by a vector to produce another vector. Scalar multiplication must satisfy the following axioms, where normal letters represent scalars and boldfaced letters represent vectors:
a(bx) = (ab)x: scalar multiplication is associative with multiplication of scalars.
1x = x: the multiplicative identity 1 in the scalar field is also an identity for scalar multiplication.
a(x+y) = ax+ay: scalar multiplication distributes over vector addition.
(a+b)x = ax+bx: scalar multiplication distributes over scalar addition.
The distributive laws imply further properties like 0x = 0 or (-1)x = -x; the proofs are essentially the same as in a field. Note that the two zeroes and the two negations in these formulas are different; on the left-hand side we are in the scalar field (or its additive group), and on the right-hand side we are in the vector space (thinking of it as a group).
When writing about vector spaces, the vectors have the starring role, and we think of a vector space V as consisting of the set of vectors, with the field of scalars often assumed to be some standard field like the reals or the complex numbers. (If we want to emphasize that the scalar field for some particular vector space V is F, we say that V is a vector space over F.) The original motivation for vectors was directions in (real, Euclidean, physical) space: in pirate terms, vector x might representing walking one pace North, vector y might represent walking three paces East, and vector 9x+12y might represent walking 9 paces north then 12*3=36 paces East in order to find the buried treasure. The assumption that vector addition is abelian says that it doesn't matter if we walk the 9x vector or the 12y vector first---this assumption may or may not world in the real world of treasure islands full of traps and pitfalls, but we should get to the same place either way in an idealized space without obstacles. The properties of vector multiplication follow from the intuition that multiplying by a scalar is "scaling" the vector---stretching it or shrinking it in its original direction by some factor determined by the particular scalar we choose.
If we replace the scalar field with a scalar ring, we get a more general structure called a module. We won't talk about these much.
For calculational purposes, we often think of vectors as sequences of coordinates, where each coordinate is an element of the field the vector space is defined over. Adding two vectors involves adding their coordinates componentwise, e.g. (1,2,3) + (30,20,10) = (31,22,13), and scalar multiplication also multiplies componentwise, e.g. 3(1,2,3) = (3,6,9). The length of each sequence is the dimension of the vector space. This approach can be taken in any vector space that has a finite basis: details are given in AbstractLinearAlgebra.
Some other examples of vector spaces:
- Any field F is a vector space over itself. The vectors are identical to the scalars, and vector multiplication is just the usual multiplication operation in the field.
- The set of functions from some fixed set S to a field F is a vector space over F, with f+g defined by (f+g)(x) = f(x)+g(x), af by (af)(x) = a*f(x), etc. Special cases of this for restricted classes of functions include random variables with values in F, continuous functions from the reals to the reals, etc.
- The ring of polynomials F[x], where F is a field, is a vector space over F with the obvious interpretation of scalar multiplication.
140.4.1. Homomorphisms of vector spaces
A homomorphism between two vector spaces over the same field is a homomorphism between the groups of vectors that also preserves scalar multiplication. In particular, this means that
For any x and y, f(x+y) = f(x)+f(y).
For any x, f(-x) = -f(x).
f(0) = 0.
For any x and scalar a, f(ax) = a*f(x).
Such homomorphisms are called linear transformations or linear maps. Linear transformations between finite-dimensional vector spaces can be represented by matrices (more on this in AbstractLinearAlgebra).
140.4.2. Subspaces
A subspace of a vector space is just a subgroup of the group of vectors that is closed under scalar multiplication, i.e. a set V'⊆V such that x+y, -x, and ax are in V' whenever x and y are, where a is any scalar. Subspaces also have an important role in AbstractLinearAlgebra and will be discussed further there.
141. Polynomials
A polynomial in a variable x over a commutative ring R is an expression of the form
![\[p(x) = \sum_{i=0}^{d} a_i x^i.\] \[p(x) = \sum_{i=0}^{d} a_i x^i.\]](/pinewiki/Polynomials?action=AttachFile&do=get&target=latex_e1f1ab815f4dbb2eaa94beb5df041b49b365a681_p1.png)
Note that a polynomial only has finitely many terms—with infinitely many terms, we get a formal power series (see GeneratingFunctions).
In any polynomial, the values ai are called the coefficients of the polynomial and each ai in particular is the coefficient of xi. The variable x generally has no role except to act as a hat-rack for exponents, although we can evaluate a polynomial by substituting a particular element of R for x. Evaluation turns a polynomial into a function from R to R, but we consider polynomials with different coefficients to be different even if they yield the same function (this usually only happens when R is finite, e.g. in ℤ2[x] the polynomials x, x2, x3, x + x2 + x37, etc. all give the same function but are still treated as distinct polynomials).
The set of all polynomials in x over R is written R[x]. It satisfies all the axioms of a commutative ring, where addition is defined by (p+q)i = pi + qi and multiplication is defined by
![\[(pq)_i = \sum_{j=0}^{i} p_j q_{j-i},\] \[(pq)_i = \sum_{j=0}^{i} p_j q_{j-i},\]](/pinewiki/Polynomials?action=AttachFile&do=get&target=latex_96049aa5fcd6e6ac0a8158df1d0baf9db9b0d63a_p1.png)
an operation on sequences known as convolution. The intuition behind this definition is that we can obtain a term xi as the product of terms xj xi-j for any j with 0 ≤ j ≤ i since the exponents add, and the sum just collects the coefficients of all such terms.
Given a polynomial p(x), the largest exponent of any term with a nonzero coefficient is called the degree of a polynomial; this is often abrreviated as deg(p(x)). The nonzero coefficient in question is called the leading coefficient of the polynomial. A nonzero constant polynomial has degree 0. It is sometimes convenient to assign the zero polynomial degree -1 or -∞, but as the behavior of the zero polynomial is messy it is usually safer just to leave its degree undefined.
It is not hard to show that for nonzero p and q, deg(p+q) ≤ max(deg(p), deg(q)) and deg(pq) ≤ deg(p) + deg(q). The second inequality becomes an equality if R is a field. The reason is that the leading coefficient of pq is the product of the leading coefficients of p and q, and in a field a product can't be zero unless one of its factors is zero. It follows that polynomials over a field do not form a field, as multiplying any polynomial p of degree 1 or higher by any other polynomial q gives a product pq with deg(pq) ≥ 1, implying pq ≠ 1: p has no multiplicative inverse. However, we will be able to construct fields as quotient rings of rings of polynomials.
142. Division of polynomials
Just like we can divide integers to get a quotient and remainder, we can also divide polynomials over a field. The division algorithm looks suspiciously like long division, which is not terribly surprising if we realize that the usual base-10 representation of a number is just a polynomial over 10 instead of x. That the division algorithm for polynomials works and gives unique results follows from a simple induction argument on the degree.
Let a and b be polynomials in F[x], where F is some field. We want to find q and r such that a = bq + r and deg(r) < deg(b) (or r = 0 if deg(b) = 0—this is where it is convenient to define deg(0) as some negative quantity). It's not hard to see that deg(q) will be exactly deg(a) - deg(b) if this quantity is non-negative, since deg(bq) = deg(q) + deg(b) and deg(r) is less, preventing it from knocking out the leading coefficient of bq. On the other hand, if deg(a) < deg(b), then q = 0 and r = a is the unique solution to a = bq+r, as for any nonzero q we would get deg(a) ≥ deg(b). This forms the basis of an inductive argument on deg(a) that there is always a unique q and r for any a and b.
Suppose deg(a) ≥ deg(b), and let the leading term of a be anxn and b be bmxm. Then an = qm-nbm since the sum defining an will contain only the product of the leading terms of b and q. We can thus solve for the unique leading coefficient qm-n = an(bm)-1. To obtain the rest of q, let a' = a - b qm-n xm-n; this new polynomial a' has degree less than a, so by the induction hypothesis there is a unique q' and r' with deg(r') < deg(b) such that a' = bq' + r'. But then a = b(qm-nxm-n + q') + r' gives the desired unique solution to a = bq+r.
Example: Let F = ℤ5 and let a = 4x2 + 2x + 1 and b = 3x + 4. What are q and r? We have q1 = 4⋅3-1 = 4⋅2 = 3. Subtracting q1x1b = 3xb from a gives a' = (4x2 + 2x + 1) - 3x(3x + 4) = (4x2 + 2x + 1) - (4x2 + 2x) = 1. This has degree less than deg(b), so we are done: 4x2 + 2x + 1 = (3x + 4)(3x) + 1, which we can verify by multiplying out 3x⋅3x + 4⋅3x + 1 = 9x2 + 12x + 1 = 4x2 + 2x + 1.
143. Divisors and greatest common divisors
A polynomial d(x) is a divisor of a polynomial p(x) if there exists some polynomial q(x) such that d(x)q(x) = p(x). A greatest common divisor of two polynomial p(x) and p'(x) is a common divisor d(x) such that any other d'(x) that divides both p(x) and p'(x) also divides d(x). Outside of ℤ2[x], a greatest common divisor of two polynomials is not unique, as the fact that our coefficients are all in a field means that if d(x)|p(x) then ad(x)|p(x) for any nonzero field element a (compute from p(x) = d(x)q(x) that p(x) = (ad(x))(a-1q(x))). However, it is possible to show using a version of the Euclidean algorithm (see NumberTheory) that a greatest common divisor of any two polynomials p(x) and p'(x) exists and is unique up to multiplication by nonzero constants (see BiggsBook §22.6). We can go one step further: the extended Euclidean algorithm also works for polynomials, and yields for each p(x), p'(x), and gcd d(x) of p(x) and p'(x) polynomials a(x) and a'(x) such that d(x) = a(x)p(x) + a'(x)p'(x).
144. Factoring polynomials
As with integers, to factor a polynomial p is to find polynomials p1, p2, ... pk such that p = p1p2⋯pk. For polynomials, the role of primes in integer factorization is taken by irreducible polynomials, where a polynomial p is irreducible if p(x) = a(x)b(x) holds only if at lest one of a(x) or b(x) has degree zero. Because the extended Euclidean algorithm works for polynomials, the same proof used to prove unique factorization for integers also works for polynomials except for the messy detail of being able to multiply factors by nonzero constants. But if we restrict our attention to monic polynomials—those whose leading coefficient is 1—then we do in fact get a unique factorization (up to reordering of factors) of each monic polynomial into monic irreducible polynomials.
Which polynomials are irreducible and how polynomials factor depends on the underlying field. In ℤ2, the polynomial x2+x+1 is irreducible: it's not equal to x(x+1) = x2+x or x⋅x = x2, and there are no other degree-1 polynomials to work with. It's also irreducible over both ℚ and ℝ, since if it factors as (x+a)(x+b), then -a and -b are both solutions to x2+x+1 = 0, and the quadratic formula gives solutions
![\[\frac{-1 \pm \sqrt{-3}}{2}\] \[\frac{-1 \pm \sqrt{-3}}{2}\]](/pinewiki/Polynomials?action=AttachFile&do=get&target=latex_d40cd9616ab82b3e2f62bf9366e65a320b4ca849_p1.png)
and there is no √(-3) in ℚ or ℝ. But it ceases to be irreducible in the field of complex numbers ℂ, since ℂ contains √(-3) = i√3. In fact, no polynomial of degree greater than 1 is irreducible in ℂ: this is why mathematicians invented the complex numbers.
To take a different example, x2 + 1 is not irreducible over ℤ2, since (x+1)(x+1) = x2 + 2x + 1 = x2+1 (mod 2). But it is irreducible in ℚ and ℝ since neither contains i = √(-1), and it factors differently as (x+i)(x-i) in ℂ.
One familiar fact about polynomials that we've been implicitly using is the following handy theorem, which holds no matter what field we are working in:
- Theorem
- Let p(x) be a nonzero polynomial over a field F. Then p(x) has a divisor (x-a) if and only if p(a) = 0.
- Proof
- The only if direction is easy: if p(x) = (x-a)q(x), then p(a) = (a-a)q(a) = 0⋅q(a) = 0. For the if direction, suppose p(a) = 0, and apply the division algorithm to obtain q(x) (a polynomial) and r (a constant) such that p(x) = (x-a)q(x) + r. Then 0 = p(a) = (a-a)q(x) + r = 0⋅q(x) + r = r. In other words, r = 0 and p(x) = (x-a)q(x) as claimed.
This can quickly be used to show that a polynomial is not irreducible: e.g. p(x) = x4 + 3x2 + 3x + 1 is not irreducible in ℤ5 because p(2) = 0 (check it and see). It follows from the theorem that (x-2) = (x+3) divides p(x). However, it is possible for a polynomial to never evaluate to zero and still not be irreducible: a simple example in ℤ2[x] would be x4 + x2 + 1 = (x2+x+1)(x2+x+1) and in ℝ[x] would be x4 + 2x2 + 1 = (x2+1)(x2+1). In both cases the big polynomial never evaluates to zero because none of its factors ever do. However, this can only happen to polynomials that have no degree-1 factors, so looking for zeros is a good test of irreducibility for polynomials of degree 3 or less.
145. The ideal generated by an irreducible polynomial
Suppose p(x) is a polynomial in F[x] for some field F. Then I(p(x)) = { a(x)p(x) | a(x) ∈ F[x] } is an ideal of the ring F[x]. (Recall from AlgebraicStructures that I(p(x)) is an ideal of F[x] if it's a subring of F[x] such that for all b(x) in I(p(x)) and c(x) in F[x], b(x)c(x) is in I(p(x)).) Clearly I(p(x)) is a subring, since a(x)p(x) + a'(x)(x) = (a(x)+a'(x))p(x) is a multiple of p(x) and a(x)p(x)⋅a'(x)p(x) is also a multiple of p(x). But it's also an ideal, since multiplying any b(x) by some a(x)p(x) yields b(x)a(x)⋅p(x) ∈ I(p(x)). It follows that there is a quotient ring F[x]/I(p(x)), usually written simply as F[x]/p(x), in which the elements are the residue classes of polynomials modulo p(x) and two polynomials are in the same residue class if and only if they differ by a multiple of p(x).
Another way of describing these residue classes is that each consists of all polynomial a(x) that yield the same remainder r(x) when divided by p(x)-just like what happens in ℤm = ℤ/mℤ, another quotient ring obtained from an ideal generated by a single element. It follows that we can represent each one by a distinct r(x) with deg(r(x)) < deg(p(x)).
If p is irreducible, something very exciting happens in this quotient ring—analogous to what happens in ℤp = ℤ/pℤ when p is prime. Each nonzero r(x) with deg(r) < deg(p) has 1 as a greatest common divisor with p, for any constant divides 1 (1 = cc-1) and any non-constant can't divide both p and r since p is irreducible. It follows from the extended Euclidean algorithm for polynomials that there exist r' and p' such that rr' + pp' = 1, or in other words that rr' is congruent to 1 mod p. It follows that every nonzero element of F[x]/p has a multiplicative inverse: F[x]/p is a field. Since we can specify an element of F[x]/p when deg(p) = n by giving the n coefficients r0, r1, ..., rn-1 of r, this field has exactly |F|n elements.
Thus to find a finite field of pn elements we can start with F = ℤp and take a quotient of F[x] with respect to some irreducible polynomial of degree n. Amazingly enough, such polynomials exist for any n. We won't prove this here but a proof is given in BiggsBook Chapter 23, which contains an extensive discussion of the construction and properties of finite fields.
We can also apply the technique of taking a quotient of F[x] with respect to an irreducible polynomials (known as field extension) to infinite fields. The most famous example is the field ℂ = ℝ[x]/(x2+1); the fact that x2+1 has degree 2 explains why all complex numbers can be written as two-term polynomials a+bx (i.e. a+bi). But we can construct other fields from other irreducible polynomials, such as the field ℚ[√2] = ℚ[x]/(x2-2), which consists of all expressions of the form a+b√2 where a and b are rational. This is a bigger field that ℚ, but it's still much smaller than ℝ: for example, it doesn't include π or even √3.
146. FiniteFields
Our goal here is to find computationally-useful structures that act enough like the rational numbers ℚ or the real numbers ℝ that we can do arithmetic in them that are small enough that we can describe any element of the structure uniquely with a finite number of bits. Such structures are called finite fields.
An example of a finite field is ℤp, the integers mod p (see ModularArithmetic). These finite fields are inconvenient for computers, which like to count in bits and prefer numbers that look like 2n to horrible nasty primes. So we'd really like finite fields of size 2n for various n, particularly if the operations of addition, multiplication, etc. have a cheap implementation in terms of sequences of bits. To get these, we will show how to construct a finite filed of size pn for any prime p and positive integer n, and then let p=2.
Contents
147. A magic trick
We will start with a magic trick. Suppose we want to generate a long sequence of bits that are hard to predict. One way to do this is using a mechanism known as a linear-feedback shift register (LFSR). There are many variants of LFSRs. Here is one that generates a sequence that repeats every 15 bits by keeping track of 4 bits of state, which we think of as a binary number r3r2r1r0.
To generate each new bit, we execute the following algorithm:
Rotate the bits of r left, to get a new number r2r1r0r3.
- If the former leftmost bit was 1, flip the new leftmost bit.
- Output the rightmost bit.
Here is the algorithm in action, starting with r = 0001:
r |
rotated r |
rotated r after flip |
output |
0001 |
0010 |
0010 |
0 |
0010 |
0100 |
0100 |
0 |
0100 |
1000 |
1000 |
0 |
1000 |
0001 |
1001 |
1 |
1001 |
0011 |
1011 |
1 |
1011 |
0111 |
1111 |
1 |
1111 |
1111 |
0111 |
1 |
0111 |
1110 |
1110 |
0 |
1110 |
1101 |
0101 |
1 |
0101 |
1010 |
1010 |
0 |
1010 |
0101 |
1101 |
1 |
1101 |
1011 |
0011 |
1 |
0011 |
0110 |
0110 |
0 |
0110 |
1100 |
1100 |
0 |
1100 |
1001 |
0001 |
1 |
0001 |
0010 |
0010 |
0 |
After 15 steps, we get back to 0001, having passed through all possible 4-bit values except 0000. The output sequence 000111101011001... has the property that every 4-bit sequence except 0000 appears starting at one of the 15 positions, meaning that after seeing any 3 bits (except 000), both bits are equally likely to be the next bit in the sequence. We thus get a sequence that is almost as long as possible given we have only 24 possible states, that is highly unpredictable, and that is cheap to generate. So unpredictable and cheap, in fact, that the governments of both the United States and Russia operate networks of orbital satellites that beam microwaves into our brains carrying signals generated by linear-feedback shift registers very much like this one. Similar devices are embedded at the heart of every modern computer, scrambling all communications between the motherboard and PCI cards to reduce the likelihood of accidental eavesdropping.
What horrifying deep voodoo makes this work?
148. Fields and rings
A field is a set F together with two operations + and ⋅ that behave like addition and multiplication in the rationals or real numbers. Formally, this means that:
Addition is associative: (x+y)+z = x+(y+z) for all x, y, z F.
There is an additive identity 0 such that 0+x = x+0 = x for all x in F.
Every x in F has an additive inverse -x such that x+(-x) = (-x)+x = 0.
Addition is commutative: x+y = y+x for all x, y in F.
Multiplication distributes over addition: x⋅(y+z) = (x⋅y + x⋅z) and (y+z)⋅x = (y⋅x + z⋅x) for all x,y, z, in F.
- Multiplication is associative: (x⋅y)⋅z = x⋅(y⋅z) for all x, y, z in F.
There is a multiplicative identity 1 such that 1⋅x = x⋅1 = x for all x in F-{0}.
- Multiplication is commutative: x⋅y = y⋅x for all x, y in F.
Every x in F-{0} has a multiplicative inverse x-1 such that x⋅x-1 = x-1⋅x = 1.
Some structures fail to satisfy all of these axioms but are still interesting enough to be given names. A structure that satisfies 1–3 is called a group; 1–4 is an abelian group; 1–7 is a ring; 1–8 is a commutative ring. In the case of groups and abelian groups there is only one operation +. There are also more exotic names for structures satisfying other subsets of the axioms; see AbstractAlgebra.
Some examples of fields: ℝ, ℚ, ℂ, ℤp where p is prime. We will be particularly interested in ℤp, since we are looking for finite fields that can fit inside a computer.
If (F,+,⋅) looks like a field except that multiplication isn't necessarily commutative and some nonzero elements might not have inverses, then it's a ring (or a commutative ring if multiplication is commutatitive). The integers ℤ are an example of a commutative ring, as is ℤm for m > 1. Square matrices of fixed dimension > 1 are an example of a non-commutative ring.
149. Polynomials over a field
Any field F generates a polynomial ring F[x] consisting of all polynomials in the variable x with coefficients in F. For example, if F = ℚ, some elements of ℚ[x] are 3/5, (22/7)x2 + 12, 9003x417 - (32/3)x4 + x2, etc. Addition and multiplication are done exactly as you'd expect, by applying the distributive law and combining like terms: (x+1)⋅(x2+3/5) = x⋅x2+x⋅(3/5)+x2+(3/5) = x3 + x2 + (3/5)x + (3/5).
The degree deg(p) of a polynomial p in F[x] is the exponent on the leading term, the term with a nonzero coefficient that has the largest exponent. Examples: deg(x2+1) = 2, deg(17) = 0. For 0, which doesn't have any terms with nonzero coefficients, the degree is taken to be -∞. Degrees add when multiplying polynomials: deg((x2+1)(x+5)) = deg(x2+1)+deg(x+5) = 2+1 = 3; this is just a consequence of the product leading terms producing the leading term of the new polynomial. For addition, we have deg(p+q) max(deg(p),deg(q)), but we can't guarantee equality (maybe the leading terms cancel).
Because F[x] is a ring, we can't do division the way we do it in a field like ℝ, but we can do division the way we do it in a ring like ℤ, leaving a remainder. The equivalent of the integer division algorithm for ℤ is:
- Division algorithm for polynomials
Given a polynomial f and a nonzero polynomial g in F[x], there are unique polynomials q and r such that f = q⋅g + r and deg(r) < deg(g).
The essential idea is that we can find q and r using the same process of long division as we use for integers. For example, in ℚ[x]:
x - 1
______________
x+2 ) x² + x + 5
x² + 2x
-------
-x + 5
-x + -5
=======
10From this we get x2 + x + 5 = (x+2)(x-1) + 10, with deg(10) = 0 < deg(x+2) = 1. We are going to use this later to define finite fields by taking F[x] modulo some well-chosen polynomial, analogously to the way we can turn ℤ (a ring) into a field ℤp by taking quotients mod p.
150. Algebraic field extensions
Given a field F, we can make a bigger field by adding in extra elements that behave in a well-defined and consistent way. An example of this is the extension of the real numbers ℝ to the complex numbers ℂ by adding i.
The general name for this trick is algebraic field extension and it works by first constructing the ring of polynomials F[x] and then smashing it down into a field by taking remainders modulo some fixed polynomial p(x). For this to work, the polynomial has to to be irreducible, which mean that p(x) = 0 if and only if x = 0, or equivalently that p can't be factored as (x+a)p' for some a and p' (which makes irreducibility sort of like being prime, and makes this construction sort of like the construction of ℤp).
The fact that the resulting object is a field follows from inheriting all the commutative ring properties from F[x], plus getting multiplicative inverses for essentially the same reason as in ℤp: we can find them using the extended Euclidean algorithm applied to polynomials instead of integers (we won't prove this).
In the case of the complex numbers ℂ, the construction is ℂ = ℝ[i]/(i2+1). Because i2+1 = 0 has no solution i∈ℝ, this makes i2+1 an irreducible polynomial. An element of ℂ is then a degree-1 or less polynomial in ℝ[i], because these are the only polynomials that survive taking the remainder mod i2+1 intact.
If you've used complex numbers before, you were probably taught to multiply them using the rule i2 = -1, which is a rewriting of i2 + 1 = 0. This is equivalent to taking remainders: (i + 1)(i + 2) = (i2 + 3i + 2) = 1⋅(i^2+1) + (3i + 1) = 3i + 1.
The same thing works for other fields and other irreducible polynomials. For example, in ℤ2, the polynomial x2+x+1 is irreducible, because x2+x+1=0 has no solution (try plugging in 0 and 1 to see). So we can construct a new finite field ℤ2[x]/(x2+x+1) whose elements are polynomials with coefficients in ℤ2 modulo x2+x+1.
Addition in ℤ2[x]/(x2+x+1) looks like vector addition<<FootNote(This is not an accident; it can be shown that that any extension field acts like a vector space over its base field.): (x+1) + (x+1) = 0⋅x + 0 = 0, (x+1) + x = 1, (1) + (x) = (x+1). Multiplication in ℤ2[x]/(x2+x+1) works by first multiplying the polynomials and taking the remainder mod (x2+x+1): (x+1)⋅(x+1) = x2+1 = 1⋅(x2+x+1) + x = x. If you don't want to take remainders, you can instead substitute x+1 for any occurrence of x2 (just like substituting -1 for i2 in ℂ), since x2+x+1 = 0 implies x2 = -x-1 = x+1 (since -1 = 1 in ℤ2).
The full multiplication table for this field looks like this:
0 |
1 |
x |
x+1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
x |
x+1 |
x |
0 |
x |
x+1 |
1 |
x+1 |
0 |
x+1 |
1 |
x |
We can see that every nonzero element has an inverse by looking for ones in the table; e.g. 1⋅1 = 1 means 1 is its own inverse and x⋅(x+1) = x2+x = 1 means that x and x+1 are inverses of each other.
Here's the same thing for ℤ2[x]/(x3+x+1):
|
0 |
1 |
x |
x + 1 |
x2 |
x2 + 1 |
x2 + x |
x2 + x + 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
x |
x + 1 |
x2 |
x2 + 1 |
x2 + x |
x2 + x + 1 |
x |
0 |
x |
x2 |
x2 + x |
x + 1 |
1 |
x2 + x + 1 |
x2 + 1 |
x + 1 |
0 |
x + 1 |
x2 + x |
x2 + 1 |
x2 + x + 1 |
x2 |
1 |
x |
x2 |
0 |
x2 |
x + 1 |
x2 + x + 1 |
x2 + x |
x |
x2 + 1 |
1 |
x2 + 1 |
0 |
x2 + 1 |
1 |
x2 |
x |
x2 + x + 1 |
x + 1 |
x2 + x |
x2 + x |
0 |
x2 + x |
x2 + x + 1 |
1 |
x2 + 1 |
x + 1 |
x |
x2 |
x2 + x + 1 |
0 |
x2 + x + 1 |
x2 + 1 |
x |
1 |
x2 + x |
x2 |
x + 1 |
Note that we now have 23 = 8 elements. In general, if we take ℤp[x] modulo a degree-n polynomial, we will get a field with pn elements. These turn out to be all the possible finite fields, with exactly one finite field for each number of the form pn (up to isomorphism, which means that we consider two fields equivalent if there is a bijection between them that preserves + and ⋅). We can refer to a finite field of size pn abstractly as GF(pn), which is an abbreviation for the Galois field of order pn.
151. Applications
So what are these things good for?
On the one hand, given an irreducible polynomial p(x) of degree n over ℤ2(x), it's easy to implement arithmetic in ℤ2[x]/p(x) GF(2n) using standard-issue binary integers. The trick is to represent each polynomial ∑ ai xi by the integer value a = ∑ ai 2i, so that each coefficient ai is just the i-th bit of a. Adding two polynomials a+b represented in this way corresponds to computing the bitwise exclusive or of a and b: a^b in programming languages that inherit their arithmetic syntax from C (i.e., almost everything except Scheme). Multiplying polynomials is more involved, although it's easy for some special cases like multiplying by x, which becomes a left-shift (a<<1) followed by XORing with the representation of our modulus if we get a 1 in the n-th place. (The general case is like this but involves doing XORs of a lot of left-shifted values, depending on the bits in the polynomial we are multiplying by.)
On the other hand, knowing that we can multiply 7 x2+x+1 by 5 x2+1 and get 6 x2+x quickly using C bit operations doesn't help us much if this product doesn't mean anything. For ModularArithmetic, we at least have the consolation that 7⋅5 = 6 (mod 29) tells us something about remainders. In GF(23), what this means is much more mysterious. This makes it useful—not in contexts where we want multiplication to make sense—but in contexts where we don't. These mostly come up in random number generation and cryptography.
151.1. Linear-feedback shift registers
Let's suppose we generate x0, x1, x2, ... in ℤ2/(x4+x3+1), which happens to be one of the finite fields isomorphic to GF(24). Since there are only 24-1 = 15 nonzero elements in GF(24), we can predict that eventually this sequence will repeat, and in fact we can show that p15 = 1 for any nonzero p using essentially the same argument as for Fermat's Little Theorem (see ModularArithmetic). So we will have x0 = x15 = x30 etc. and thus will expect our sequence to repeat every 15 steps (or possibly some factor of 15, if we are unlucky).
To compute the actual sequence, we could write out full polynomials: 1, x, x2, x3, x3+1, x3+x+1, ..., but this gets tiresome fast. So instead we'd like to exploit our representation of ∑ aixi as ∑ ai2i.
Now multiplying by x is equivalent to shifting left (i.e. multiplying by 2) followed by XORing with 11001, the binary representation of x4 + x3 + 1, if we get a bit in the x4 place that we need to get rid of. For example, we might do:
1101 (initial value) 11010 (after shift) 0011 (after XOR with 11001)
or
0110 (initial value) 01100 (after shift) 1100 (no XOR needed)
If we write our initial value as r3r2r1r0, the shift produces a new value r3r2r1r00. XORing with 11001 has three effects: (a) it removes a leading 1 if present; (b) it sets the rightmost bit to r3; and (c) it flips the new leftmost bit if r3 = 1. Steps (a) and (b) turn the shift into a rotation. Step (c) is the mysterious flip from our sequence generator. So in fact what our magic sequence generator was doing was just computing all the powers of x in a particular finite field.
As in ℤp, these powers of an element bounce around unpredictably, which makes them a useful (though cryptographically very weak) pseudorandom number generator. Because high-speed linear-feedback shift registers are very cheap to implement in hardware, they are used in applications where a pre-programmed, statistically smooth sequence of bits is needed, as in the Global Positioning System and to scramble electrical signals in computers to reduce radio-frequency interference.
151.2. Checksums
Shifting an LFSR corresponds to multiplying by x. If we also add 1 from time to time, we can build any polynomial we like, and get the remainder mod m; for example, to compute the remainder of 100101 mod 11001 we do
0000 (start with 0) 00001 (shift in 1) 0001 (no XOR) 00010 (shift in 0) 0010 (no XOR) 00100 (shift in 0) 0100 (no XOR) 01001 (shift in 1) 1001 (no XOR) 10010 (shift in 0) 1011 (XOR with 11001) 10111 (shift in 1) 1110 (XOR with 11001)
and we have computed that the remainder of x5 + x3 + 1 mod x4 + x3 + 1 is x3 + x2 + x.
This is the basis for Cyclic redundancy check checksums, which are used to detect accidental corruption of data. The idea is that we feed our data stream into the LFSR as the coefficients of some gigantic polynomial, and the checksum summarizing the data is the state when we are done. Since it's unlikely that a random sequence of flipped or otherwise damaged bits would equal 0 mod m, most non-malicious changes to the data will be visible by producing an incorrect checksum.
151.3. Cryptography
GF(2n) can also substitute for ℤp in some cryptographic protocols. An example would be the function f(s) = xs (mod m), which is fairly easy to compute in ℤp and even easier to compute in GF(2n), but which seems to be hard to invert in both cases. Here we can take advantage of the fast remainder operation provided by LFSRs to avoid having to do expensive division in ℤ.
152. LinearAlgebra
153. Matrices
We've seen that a sequence a1, a2, ..., an is really just a function from some index set ({1..n} in this case) to some codomain, where ai = a(i) for each i. What if we have two index sets? Then we have a two-dimensional structure:
![\[
A =
\left[
\begin{array}{cc}
A_{11} & A_{12} \\
A_{21} & A_{22} \\
A_{31} & A_{32}
\end{array}
\right]
\] \[
A =
\left[
\begin{array}{cc}
A_{11} & A_{12} \\
A_{21} & A_{22} \\
A_{31} & A_{32}
\end{array}
\right]
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_9d8b79fcbe79d647c359e10027d53ede9be57c01_p1.png)
where Aij = a(i,j) and the domain of the function is just the cross-product of the two index sets. Such a structure is called a matrix. The values Aij are called the elements or entries of the matrix. A sequence of elements with the same first index is called a row of the matrix; similarly, a sequence of elements with the same second index is called a column. The dimension of the matrix specifies the number of rows and the number of columns: the matrix above has dimension (3,2), or, less formally, it is a 3×2 matrix.23 A matrix is square if it has the same number of rows and columns.
Note: The convention in matrix indices is to count from 1 rather than 0. In ComputerScience terms, matrices are written in FORTRAN.
By convention, variables representing matrices are usually written with capital letters. (This is to distinguish them from lower-case scalars, which are single numbers.)
153.1. Interpretation
We can use a matrix any time we want to depict a function of two arguments (over small finite sets if we want it to fit on one page). A typical example (that predates the formal notion of a matrix by centuries) is a table of distances between cities or towns, such as this example from 1807:24
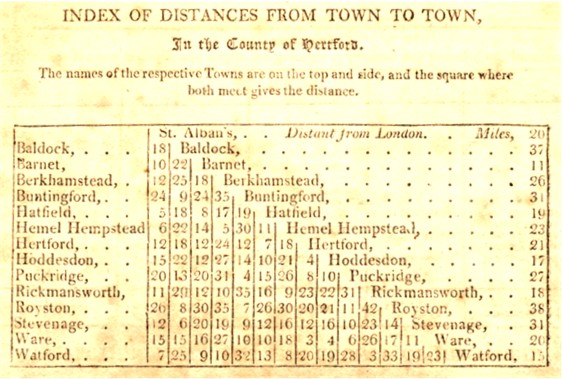
Because distance matrices are symmetric (see below), usually only half of the matrix is actually printed.
Another example would be a matrix of counts. Suppose we have a set of destinations D and a set of origins O. For each pair (i,j) ∈ D×O, let Cij be the number of different ways to travel from j to i. For example, let origin 1 be Bass Library, origin 2 be AKW, and let destinations 1, 2, and 3 be Bass, AKW, and SML. Then there is 1 way to travel between Bass and AKW (walk), 1 way to travel from AKW to SML (walk), and 2 ways to travel from Bass to SML (walk above-ground or below-ground). If we assume that we are not allowed to stay put, there are 0 ways to go from Bass to Bass or AKW to AKW, giving the matrix
![\[
C =
\left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
2 & 1
\end{array}
\right]
\] \[
C =
\left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
2 & 1
\end{array}
\right]
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_04d95b0f47e90759b66871b8a3c1361626aacc1f_p1.png)
Wherever we have counts, we can also have probabilities. Suppose we have a particle that moves between positions 1..n by flipping a coin, and moving up with probability ½ and down with probability ½ (staying put if it would otherwise move past the endpoints). We can describe this process by a transition matrix P whose entry Pij gives the probability of moving to i starting from j. For example, for n = 4, the transition matrix is
![\[
P =
\left[
\begin{array}{cccc}
1/2 & 1/2 & 0 & 0 \\
1/2 & 0 & 1/2 & 0 \\
0 & 1/2 & 0 & 1/2 \\
0 & 0 & 1/2 & 1/2
\end{array}
\right].
\] \[
P =
\left[
\begin{array}{cccc}
1/2 & 1/2 & 0 & 0 \\
1/2 & 0 & 1/2 & 0 \\
0 & 1/2 & 0 & 1/2 \\
0 & 0 & 1/2 & 1/2
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_2680f09f623d1c893bd9f8fbccf7ee5b0fe1eb3c_p1.png)
Finally, the most common use of matrices in linear algebra is to represent the coefficients of a linear transformation, which we will describe later.
153.2. Operations on matrices
153.2.1. Transpose of a matrix
The transpose of a matrix A, written A' or AT, is obtained by reversing the indices of the original matrix; (A')ij = Aji for each i and j. This has the effect of turning rows into columns and vice versa:
![\[
A' =
\left[
\begin{array}{cc}
A_{11} & A_{12} \\
A_{21} & A_{22} \\
A_{31} & A_{32}
\end{array}
\right]'
=
\left[
\begin{array}{ccc}
A_{11} & A_{21} & A_{31} \\
A_{12} & A_{22} & A_{32} \\
\end{array}
\right]
\] \[
A' =
\left[
\begin{array}{cc}
A_{11} & A_{12} \\
A_{21} & A_{22} \\
A_{31} & A_{32}
\end{array}
\right]'
=
\left[
\begin{array}{ccc}
A_{11} & A_{21} & A_{31} \\
A_{12} & A_{22} & A_{32} \\
\end{array}
\right]
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_b7cda50da4e55fc8527df9494a3f4e5eef65df35_p1.png)
If a matrix is equal to its own transpose (i.e., if Aij = Aji for all i and j), it is said to be symmetric. The transpose of an n×m matrix is an m×n matrix, so only square matrices can be symmetric.
153.2.2. Sum of two matrices
If we have two matrices A and B with the same dimension, we can compute their sum A+B by the rule (A+B)ij = Aij+Bij. Another way to say this is that matrix sums are done term-by-term: there is no interaction between entries with different indices.
For example, suppose we have the matrix of counts C above of ways of getting between two destinations on the Yale campus. Suppose that upperclassmen are allowed to also take the secret Science Hill Monorail from the sub-basement of Bass Library to the sub-basement of AKW. We can get the total number of ways an upperclassman can get from each origin to each destination by adding to C a second matrix M giving the paths involving monorail travel:
![\[
C+M =
\left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
2 & 1
\end{array}
\right]
+
\left[
\begin{array}{cc}
0 & 0 \\
1 & 0 \\
0 & 0
\end{array}
\right]
=
\left[
\begin{array}{cc}
0 & 1 \\
2 & 0 \\
2 & 1
\end{array}
\right].
\] \[
C+M =
\left[
\begin{array}{cc}
0 & 1 \\
1 & 0 \\
2 & 1
\end{array}
\right]
+
\left[
\begin{array}{cc}
0 & 0 \\
1 & 0 \\
0 & 0
\end{array}
\right]
=
\left[
\begin{array}{cc}
0 & 1 \\
2 & 0 \\
2 & 1
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_08027a49895bb295319305a7e2f0690589c35477_p1.png)
153.2.3. Product of two matrices
Suppose we are not content to travel once, but have a plan once we reach our destination in D to travel again to a final destination in some set F. Just as we constructed the matrix C (or C+M, for monorail-using upperclassmen) counting the number of ways to go from each point in O to each point in D, we can construct a matrix Q counting the number of ways to go from each point in D to each point in F. Can we combine these two matrices to compute the number of ways to travel O→D→F?
The resulting matrix is known as the product QC. We can compute each entry in QC by taking a sum of products of entries in Q and C. Observe that the number of ways to get from k to i via some single intermediate point j is just QijCjk. To get all possible routes, we have to sum over all possible intermediate points, giving (QC)ik = ∑j QijCjk.
This gives the rule for multiplying matrices in general: to get (AB)ik, sum AijBjk over all intermediate values j. This works only when the number of columns in A is the same as the number of rows in B (since j has to vary over the same range in both matrices), i.e. when A is an n×m matrix and B is an m×s matrix for some n, m, and s. If the dimensions of the matrices don't match up like this, the matrix product is undefined. If the dimensions do match, they are said to be compatible.
For example, let B = (C+M) from the sum example and let A be the number of ways of getting from each of destinations 1 = Bass, 2 = AKW, and 3 = SML to final destinations 1 = Heaven and 2 = Hell. After consulting with appropriate representatives of the Divinity School, we determine that one can get to either Heaven or Hell from any intermediate destination in one way by dying (in a state of grace or sin, respectively), but that Bass Library provides the additional option of getting to Hell by digging. This gives a matrix
![\[
A =
\left[
\begin{array}{ccc}
1 & 1 & 1 \\
2 & 1 & 1
\end{array}
\right].
\] \[
A =
\left[
\begin{array}{ccc}
1 & 1 & 1 \\
2 & 1 & 1
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_89843cf5404cfa3e81768ee1794093b981ddfdd4_p1.png)
We can now compute the product
![\[
A(C+M)
=
\left[
\begin{array}{ccc}
1 & 1 & 1 \\
2 & 1 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
0 & 1 \\
2 & 0 \\
2 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
1 \cdot 0 + 1 \cdot 2 + 1 \cdot 2 & 1 \cdot 1 + 1 \cdot 0 + 1 \cdot 1 \\
2 \cdot 0 + 1 \cdot 2 + 1 \cdot 2 & 2 \cdot 1 + 1 \cdot 0 + 1 \cdot 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
4 & 2 \\
4 & 3
\end{array}
\right].
\] \[
A(C+M)
=
\left[
\begin{array}{ccc}
1 & 1 & 1 \\
2 & 1 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
0 & 1 \\
2 & 0 \\
2 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
1 \cdot 0 + 1 \cdot 2 + 1 \cdot 2 & 1 \cdot 1 + 1 \cdot 0 + 1 \cdot 1 \\
2 \cdot 0 + 1 \cdot 2 + 1 \cdot 2 & 2 \cdot 1 + 1 \cdot 0 + 1 \cdot 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
4 & 2 \\
4 & 3
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_604b5db1bd4d2b00a7d1637474a47071590eb6eb_p1.png)
One special matrix I (for each dimension n×n) has the property that IA = A and BI = B for all matrices A and B with compatible dimension. This matrix is known as the identity matrix, and is defined by the rule Iii = 1 and Iij = 0 for i≠j. It is not hard to see that in this case (IA)ij = ∑k IikAkj = IiiAij = Aij, giving IA = A; a similar computation shows that BI = B. With a little more effort (omitted here) we can show that I is the unique matrix with this identity property.
153.2.4. The inverse of a matrix
A matrix A is invertible if there exists a matrix A-1 such that AA-1 = A-1A = 1. This is only possible if A is square (because otherwise the dimensions don't work) and may not be possible even then. Note that it is enough to find a matrix such that A-1A = I.
To try to invert a matrix, we start with the pair of matrices A, I (where I is the identity matrix defined above) and multiply both sides of the pair from the left by a sequence of transformation matrices B1, B2, ... Bk until BkBk-1⋯B1A = I. At this point the right-hand matrix will be BkBk-1⋯B1 = A-1. (We could just keep track of all the Bi, but it's easier to keep track of their product.)
How do we pick the Bi? These will be matrices that (a) multiply some row by a scalar, (b) add a multiple of one row to another row, or (c) swap two rows. We'll use the first kind to make all the diagonal entries equal one, and the second kind to get zeroes in all the off-diagonal entries. The third kind will be saved for emergencies, like getting a zero on the diagonal.
That the operations (a), (b), and (c) correspond to multiplying by a matrix is provable but tedious.25 Given these operations, we can turn any invertible matrix A into I by working from the top down, rescaling each row i using a type (a) operation to make Aii = 1, then using a type (b) operation to subtract Aji times row i from each row j > i to zero out Aji, then finally repeating the same process starting at the bottom to zero out all the entries above the diagonal. The only way this can fail is if we hit some Aii = 0, which we can swap with a nonzero Aji if one exists (using a type (c) operation). If all the rows from i on down have a zero in the i column, then the original matrix A is not invertible. This entire process is known as Gauss-Jordan elimination.
This procedure can be used to solve matrix equations: if AX = B, and we know A and B, we can compute X by first computing A-1 and then multiplying X = A-1AX = A-1B. If we are not interested in A-1 for its own sake, we can simplify things by substituting B for I during the Gauss-Jordan elimination procedure; at the end, it will be transformed to X.
153.2.4.1. Example
Original A is on the left, I on the right.
![Initial matrices:
\[
\left[
\begin{array}{ccc}
2 & 0 & 1 \\
1 & 0 & 1 \\
3 & 1 & 2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
Divide top row by 2:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
1 & 0 & 1 \\
3 & 1 & 2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
Subtract top row from middle row and 3*top row from bottom row:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 0 & 1/2 \\
0 & 1 & 1/2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-1/2 & 1 & 0 \\
-3/2 & 0 & 1
\end{array}
\right]
\]
Swap middle and bottom rows:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 1 & 1/2 \\
0 & 0 & 1/2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-3/2 & 0 & 1 \\
-1/2 & 1 & 0
\end{array}
\right]
\]
Multiply bottom row by 2:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 1 & 1/2 \\
0 & 0 & 1
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-3/2 & 0 & 1 \\
-1 & 2 & 0
\end{array}
\right]
\]
Subtract (1/2)*bottom row from top and middle rows:
\[
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1 & -1 & 0 \\
-1 & -1 & 1 \\
-1 & 2 & 0
\end{array}
\right]
\] Initial matrices:
\[
\left[
\begin{array}{ccc}
2 & 0 & 1 \\
1 & 0 & 1 \\
3 & 1 & 2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
Divide top row by 2:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
1 & 0 & 1 \\
3 & 1 & 2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
Subtract top row from middle row and 3*top row from bottom row:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 0 & 1/2 \\
0 & 1 & 1/2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-1/2 & 1 & 0 \\
-3/2 & 0 & 1
\end{array}
\right]
\]
Swap middle and bottom rows:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 1 & 1/2 \\
0 & 0 & 1/2
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-3/2 & 0 & 1 \\
-1/2 & 1 & 0
\end{array}
\right]
\]
Multiply bottom row by 2:
\[
\left[
\begin{array}{ccc}
1 & 0 & 1/2 \\
0 & 1 & 1/2 \\
0 & 0 & 1
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1/2 & 0 & 0 \\
-3/2 & 0 & 1 \\
-1 & 2 & 0
\end{array}
\right]
\]
Subtract (1/2)*bottom row from top and middle rows:
\[
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\quad
\left[
\begin{array}{ccc}
1 & -1 & 0 \\
-1 & -1 & 1 \\
-1 & 2 & 0
\end{array}
\right]
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_c371ce834080d3b39e6d0032e291765c3840704b_p1.png)
and we're done. (It's probably worth multiplying the original A by the alleged A-1 to make sure that we didn't make a mistake.)
153.2.5. Scalar multiplication
Suppose we have a matrix A and some constant c. The scalar product cA is given by the rule (cA)ij = cAij; in other words, we multiply (or scale) each entry in A by c. The quantity c in this context is called a scalar; the term scalar is also used to refer to any other single number that might happen to be floating around.
Note that if we only have scalars, we can pretend that they are 1×1 matrices; a+b = a11 + b1 and ab = a11b11. But this doesn't work if we multiply a scalar by a matrix, since cA (where c is considered to be a matrix) is only defined if A has only one row. Hence the distinction between matrices and scalars.
153.3. Matrix identities
For the most part, matrix operations behave like scalar operations, with a few important exceptions:
- Matrix multiplication is only defined for matrices with compatible dimensions.
Matrix multiplication is not commutative: in general, we do not expect that AB = BA. This is obvious when one or both of A and B is not square (one of the products is undefined because the dimensions aren't compatible), but it's also true even if A and B are both square. For a simple example of a non-commutative pair of matrices, consider
![\[
\left[
\begin{array}{cc}
1 & 1 \\
0 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
2 & 0 \\
1 & 1
\end{array}
\right]
\neq
\left[
\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
1 & 1 \\
0 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
1 & 0 \\
1 & 2
\end{array}
\right].
\] \[
\left[
\begin{array}{cc}
1 & 1 \\
0 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
2 & 0 \\
1 & 1
\end{array}
\right]
\neq
\left[
\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}
\right]
\left[
\begin{array}{cc}
1 & 1 \\
0 & 1
\end{array}
\right]
=
\left[
\begin{array}{cc}
1 & 0 \\
1 & 2
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_0e4afc15e8fb68679b89a7a732d75d85b1089dc8_p1.png)
On the other hand, matrix multiplication is associative: A(BC) = (AB)C. The proof is by expansion of the definition. First compute (A(BC))ij = ∑k Aik(BC)kj = ∑k∑m AikBkmCmj. Then compute ((AB)C)ij = ∑m (AB)imCmj = ∑m∑k AikBkmCmj = ∑k∑m AikBkmCmj = (A(BC))ij.
So despite the limitations due to non-compatibility and non-commutativity, we still have:
- Associative laws
- A+(B+C) = (A+B)+C (easy), (AB)C = A(BC) (see above). Also works for scalars: c(AB) = (cA)B = A(cB) and (cd)A = c(dA) = d(cA).
- Distributive laws
- A(B+C) = AB+BC, A(B+C) = AB+AC. Also works for scalars: c(A+B) = cA+cB, (c+d)A = cA+dA.
- Additive identity
- A+0 = 0+A = A, where 0 is the all-zero matrix of the same dimension as A.
- Multiplicative identity
- AI = A, IA = A, 1A = A, A1 = A, where I is the identity matrix of appropriate dimension in each case and 1 is the scalar value 1.
- Inverse of a product
(AB)-1 = B-1A-1. Proof: (B-1A-1)(AB) = B-1(A-1A)B = B-1(IB) = B-1B = I, and similarly for (AB)(B-1A-1).
- Transposes
(A+B)' = A'+B' (easy), (AB)' = B'A' (a little trickier). (A-1)' = (A')-1, provided A-1 exists (proof: A'(A-1)' = (A-1A)' = I' = I).
Using these identities, we can do arithmetic on matrices without knowing what their actual entries are, so long as we are careful about non-commutativity. So for example we can compute
(A+B)2 = (A+B)(A+B) = A2+AB+BA+B2.
Similarly, if for square A we have
S = ∑n∈ℕ An,
(where A0=I) we can solve the equation
- S = I + AS
by first subtracting AS from both sides to get
- IS - AS = I
then applying the distributive law:
- (I-A)S = I
and finally multiplying both sides from the left by (I-A)-1 to get
S = (I-A)-1,
assuming I-A is invertible.
154. Vectors
A 1×n or n×1 matrix is called a vector. A 1×n matrix is called a row vector for obvious reasons; similarly, an n×1 matrix is called a column vector.
Vectors behave exactly like matrices in every respect; however, they are often written with lowercase letters to distinguish them from their taller and wider cousins. If this will cause confusion with scalars, we can disambiguate by writing vectors with a little arrow on top:
![\[\vec{x}\] \[\vec{x}\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_1625b7abbfce016eab05f16ea22203b94ca1983b_p1.png)
or in boldface: x. Often we will just hope it will be obvious from context which variables represent vectors and which represent scalars, since writing all the little arrows can take a lot of time.
When extracting individual coordinates from a vector, we omit the boring index and just write x1, x2, etc. This is done for both row and column vectors, so rather than write x'i we can just write xi.
154.1. Geometric interpretation
We can use a vector to represent the coordinates of a point in space. In general, given some point in the n-dimensional Euclidean space ℝn, we consider it as an n×1 column vector (row vectors work too, but the convention is to use column vectors because it makes the matrix-vector product Ax look like function application). The set of all such vectors for a given fixed dimension form a vector space.
For example, we could represent the latitude and longitude of the major world landmarks Greenwich Observatory, Mecca, and Arthur K. Watson Hall by the column vectors
![$\left[\begin{array}{c} 0.0 \\ 0.0 \end{array}\right]$,
$\left[\begin{array}{c} 21.45 \\ 39.82 \end{array}\right]$, and
$\left[\begin{array}{c} 41.31337 \\ -72.92508 \end{array}\right]$. $\left[\begin{array}{c} 0.0 \\ 0.0 \end{array}\right]$,
$\left[\begin{array}{c} 21.45 \\ 39.82 \end{array}\right]$, and
$\left[\begin{array}{c} 41.31337 \\ -72.92508 \end{array}\right]$.](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_02198442ea4988566442fa957aa19bde50e9f22b_p1.png)
Pedantic note: The surface of the Earth is not really a Euclidean space, despite the claims of the Flat Earth Society.
In running text, we can represent these column vectors as transposed row vectors, e.g. [21.45 39.82]' for the coordinates of Mecca. Quite often we will forget whether we are dealing with a column vector or a row vector specifically and just write the sequence of entries, e.g. (21.54 39.82) or (21.54, 39.82).
We can use vectors to represent any quantities that can be expressed as a sequence of coordinates in ℝ (or more generally, over any field: see AlgebraicStructures and AbstractLinearAlgebra). A common use is to represent offsets—the difference between the coordinates of two locations—and velocities—the rate at which the coordinates of a moving object change over time. So, for example, we might write the velocity of a car that is moving due northeast at 100 km/h as the vector (100/√2 100/√2)', where each entry corresponds to the speed if we look only at the change in the north-south or west-east position. We can also think of coordinates of points as themselves offsets from some origin at position 0—Greenwich Observatory in the case of latitude and longitude.
154.2. Sums of vectors
We can add vectors term-by-term just as we can add any other matrices. For vectors representing offsets (or velocities) the geometric interpretation of x+y is that we attach y to the end of x (or vice versa, since addition is commutative) and take the combined offset, as in this picture:
*
/^
/ |
/ |
x+y/ |y
/ |
/ |
/ |
0——————>*
xThis can be used to reduce the complexity of pirate-treasure instructions:
Yargh! Start at the olde hollow tree on Dead Man's Isle, if ye dare.
- Walk 10 paces north.
- Walk 5 paces east.
- Walk 20 paces south.
- Walk 6√2 paces northwest.
- Dig 8 paces down.
- Climb back up 6 paces. There be the treasure, argh!
In vector notation, this becomes:
- (0 0 0)'
- + (10 0 0)'
- + (0 5 0)'
- + (-20 0 0)'
- + (6 -6 0)'
- + (0 0 -8)'
- + (0 0 6)
which sums to (-4 -1 -2)'. So we can make our life easier by walking 4 paces south, 1 pace west, and digging only 2 paces down.
154.3. Length
The length of a vector x, usually written as ‖x‖ or sometimes just |x|, is defined as √(∑i xi); the definition follows from the Pythagorean theorem (length)2 = ∑ (coordinates)2. Because the coordinates are squared, all vectors have non-negative length, and only the zero vector has length 0.
Length interacts with scalar multiplication exactly as you would expect: ‖cx‖ = c‖x‖. The length of the sum of two vectors depends on how the are aligned with each other, but the triangle inequality ‖x+y‖ ≤ ‖x‖+‖y‖ always holds.
A special class of vectors are the unit vectors, those vectors x for which ‖x‖ = 1. In geometric terms, these correspond to all the points on the surface of a radius-1 sphere centered at the origin. Any vector x can be turned into a unit vector x/‖x‖ by dividing by its length. In two dimensions, the unit vectors are all of the form (x y)' = (cos Θ, sin Θ)', where by convention Θ is the angle from due east measured counterclockwise; this is why traveling 9 units northwest corresponds to the vector 9(cos 135°, sin 135°)' = (-9/√2, 9/√2)'. In one dimension, the unit vectors are (±1). (There are no unit vectors in zero dimensions: the unique zero-dimensional vector has length 0.)
154.4. Dot products and orthogonality
Suppose we have some column vector x, and we want to know how far x sends us in a particular direction, where the direction is represented by a unit column vector e. We can compute this distance (a scalar) by taking the dot product
e⋅x = e'x = ∑ eixi.
For example, x = (3 4)' and e = (1 0)', then the dot product is
![\[
e\cdot x = \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} 3 \\ 4 \end{array}\right] = 1\cdot 3 + 0 \cdot 4 = 3.
\] \[
e\cdot x = \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} 3 \\ 4 \end{array}\right] = 1\cdot 3 + 0 \cdot 4 = 3.
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_d9a0cdfca4c0dc07ce4e1a449e8cdb60f16a14b2_p1.png)
In this case we see that the (1 0)' vector conveniently extracts the first coordinate, which is about what we'd expect. But we can also find out how far x takes us in the (1/√2 1/√2)' direction: this is (1/√2 1/√2)x = 7/√2.
By convention, we are allowed to take the dot product of two row vectors or of a row vector times a column vector or vice versa, provided of course that the non-boring dimensions match. In each case we transpose as appropriate to end up with a scalar when we take the matrix product.
Nothing in the definition of the dot product restricts either vector to be a unit vector. If we compute x⋅y where x = ce and ‖e‖ = 1, then we are effectively multiplying e⋅y by c. It follows that the dot product is proportional to the length of both of its arguments. This often is expressed in terms of the geometric formulation, memorized by vector calculus students since time immemorial:
The dot product of x and y is equal to the product of their lengths times the cosine of the angle between them.
This formulation is a little misleading, since modern geometers will often define the angle between two vectors x and y as cos-1(x⋅y/(‖x‖⋅‖y‖)), but it gives a good picture of what is going on. One can also define the dot-product as the area of the parallelogram with sides x and y, with the complication that if the parallelogram is flipped upside-down we treat the area as negative. The simple version in terms of coordinates is harder to get confused about, so we'll generally stick with that.
Two vectors are orthogonal if their dot product is zero. In geometric terms, this occurs when either one or both vectors is the zero vector or when the angle between them is ±90° (since cos(±90°) = 0). In other words, two non-zero vectors are orthogonal if and only if they are perpendicular to each other.
Orthogonal vectors satisfy the Pythagorean theorem: If x⋅y = 0, then ‖x+y‖2 = (x+y)⋅(x+y) = x⋅x + x⋅y + y⋅x + y⋅y = x⋅x + y⋅y = ‖x‖2 + ‖y‖2. It is not hard to see that the converse is also true: any pair of vectors for which ‖x+y‖2 = ‖x‖2 + ‖y‖2 must be orthogonal (at least in ℝn).
Orthogonality is also an important property of vectors used to define coordinate systems, as we will see below.
155. Linear combinations and subspaces
A linear combination of a set of vectors x1...xn is any vector that can be expressed as ∑ cixi for some coefficients ci. The span of the vectors, written <x1...xn>, is the set of all linear combinations of the xi.26
The span of a set of vectors forms a subspace of the vector space, where a subspace is a set of vectors that is closed under linear combinations. This is a succinct way of saying that if x and y are in the subspace, so is ax+by for any scalars a and b. We can prove this fact easily: if x = ∑ cixi and y = ∑ dixi, then ax+by = ∑ (aci+bdi)xi.
A set of vectors x1, x2, ..., xn is linearly independent if there is no way to write one of the vectors as a linear combination of the others, i.e. if there is no choice of coefficients that makes some xi = ∑j≠i cjxj. An equivalent definition is that there is no choice of coefficients ci such that ∑ cixi = 0 and at least one ci is nonzero (to see the equivalence, subtract xi from both sides of the xi = ∑ cjxj equation).
155.1. Bases
If a set of vectors is both (a) linearly independent, and (b) spans the entire vector space, then we call that set of vectors a basis of the vector space. An example of a basis is the standard basis consisting of the vectors (0 0 ... 0 1)', (0 0 ... 1 0)', ..., (0 1 ... 0 0)', (1 0 ... 0 0)'. This has the additional nice property of being made of of vectors that are all orthogonal to each other (making it an orthogonal basis) and of unit length (making it a normal basis).
A basis that is both orthogonal and normal is called orthonormal. We like orthonormal bases because we can recover the coefficients of some arbitrary vector v by taking dot-products. If v = ∑ aixi, then v⋅xj = ∑ ai(xi⋅xj) = ai, since orthogonality means that xi⋅xj=0 when i≠j, and normality means xi⋅xi = ‖xi‖2 = 1.
However, even for non-orthonormal bases it is still the case that any vector can be written as a unique linear combination of basis elements. This fact is so useful we will state it as a theorem:
- Theorem
If {xi} is a basis for some vector space V, then every vector y has a unique representation y = a1x1 + a2x2 + ... + anxn.
- Proof
Suppose there is some y with more than one representation, i.e. there are sequences of coefficients ai and bi such that y = a1x1 + a2x2 + ... + anxn = b1x1 + b2x2 + ... + bnxn. Then 0 = y-y = a1x1 + a2x2 + ... + anxn - b1x1 + b2x2 + ... + bnxn = (a1-b1)x1 + (a2-b2)x2 + ... + (an-bn)xn. But since the xi are independent, the only way a linear combination of the xi can equal 0 is if all coefficients are 0, i.e. if ai = bi for all i.
Even better, we can do all of our usual vector space arithmetic in terms of the coefficients ai. For example, if a = ∑aixi and b = ∑bixi, then it can easily be verified that a+b = ∑(ai+bi)xi and ca = ∑(cai)xi.
However, it may be the case that the same vector will have different representations in different bases. For example, in ℝ2, we could have a basis B1 = { (1,0), (0,1) } and a basis B2 = { (1,0), (1,-2) }. The vector (2,3) would be represented as (2,3) using basis B1 but would be represented as (5/2,-3/2) in basis B2. In the standard basis { (1,0), (0,1) }, the representation of (2,3) is just (2,3).
Both bases above have the same size. This is not an accident; if a vector space has a finite basis, then all bases have the same size. We'll state this as a theorem, too:
- Theorem
Let x1...xn and y1...ym be two finite bases of the same vector space V. Then n=m.
- Proof
Assume without loss of generality that n ≤ m. We will show how to replace elements of the xi basis with elements of the yi basis to produce a new basis consisting only of y1...yn. Start by considering the sequence y1,x1...xn. This sequence is not independent since y1 can be expressed as a linear combination of the xi (they're a basis). So from Theorem 1 there is some xi that can be expressed as a linear combination of y1,x1...xi-1. Swap this xi out to get a new sequence y1,x1...xi-1,xi+1,...xn. This new sequence is also a basis, because (a) any z can be expressed as a linear combination of these vectors by substituting the expansion of xi into the expansion of z in the original basis, and (b) it's independent, because if there is some nonzero linear combination that produces 0 we can substitute the expansion of xi to get a nonzero linear combination of the original basis that produces 0 as well. Now continue by constructing the sequence y2,y1,x1...xi-1,xi+1,...xn, and arguing that some xi' in this sequence must be expressible as a combination of earlier terms by Theorem 1 (it can't be y1 because then y2y1 is not independent), and drop this xi'. By repeating this process we can eventually eliminate all the xi, leaving the basis yn,...,y1. But then any yk for k > n would be a linear combination of this basis, so we must have m = n.
The size of any basis of a vector space is called the dimension of the space.
156. Linear transformations
When we multiply a column vector by a matrix, we transform the vector into a new vector. This transformation is linear in the sense that A(x+y) = Ax + Ay and A(cx) = cAx; thus we call it a linear transformation. Conversely, any linear function f from column vectors to column vectors can be written as a matrix M such that f(x) = Mx. We can prove this by decomposing each x using the standard basis.
- Theorem
Let f:ℝn→ℝm be a linear transformation. Then there is a unique n×m matrix M such that f(x) = Mx for all column vectors x.
- Proof
We'll use the following trick for extracting entries of a matrix by multiplication. Let M be an n×m matrix, and let ei be a column vector with eij = 1 if i=j and 0 otherwise.27 Now observe that (ei)'Mej = ∑k eik (Mej)k = (Mej)i = ∑k Mikejk = Mij. So given a particular linear f, we will now define M by the rule Mij = (ei)'f(ej). It is not hard to see that this gives f(ej) = Mej for each basis vector j, since multiplying by (ei)' grabs the i-th coordinate in each case. To show that Mx = f(x) for all x, decompose each x as ∑k ckek. Now compute f(x) = f(∑k ckek) = ∑k ckf(ek) = ∑k ckM(ek) = M(∑k ckek) = Mx.
156.1. Composition
What happens if we compose two linear transformations? We multiply the corresponding matrices:
(g∘f)(x) = g(f(x)) = g(Mfx) = Mg(Mfx) = (MgMf)x.
This gives us another reason why the dimensions have to be compatible to take a matrix product: If multiplying by an n×m matrix A gives a map g:ℝm→ℝn, and multiplying by a k×l matrix B gives a map f:ℝl→ℝk, then the composition g∘f corresponding to AB only works if m = k.
156.2. Role of rows and columns of M in the product Mx
When we multiply a matrix and a column vector, we can think of the matrix as a sequence of row or column vectors and look at how the column vector operates on these sequences.
Let Mi⋅ be the i-th row of the matrix (the "⋅" is a stand-in for the missing column index). Then we have
(Mx)i = ∑k Mikxk = Mi⋅⋅x.
So we can think of Mx as a vector of dot-products between the rows of M and x:
![\[
\left[
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
\right]
\left[
\begin{array}{c}
1 \\ 1 \\ 2
\end{array}
\right]
=
\left[
\begin{array}{c}
(1, 2, 3)\cdot(1, 1, 2) \\
(4, 5, 6)\cdot(1, 1, 2)
\end{array}
\right]
=
\left[
\begin{array}{c}
9 \\ 21
\end{array}
\right].
\] \[
\left[
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
\right]
\left[
\begin{array}{c}
1 \\ 1 \\ 2
\end{array}
\right]
=
\left[
\begin{array}{c}
(1, 2, 3)\cdot(1, 1, 2) \\
(4, 5, 6)\cdot(1, 1, 2)
\end{array}
\right]
=
\left[
\begin{array}{c}
9 \\ 21
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_b4ee9149cc206cc8f73a67cea57eb7d6c81b829b_p1.png)
Alternatively, we can work with the columns M⋅j of M. Now we have
(Mx)i = ∑k Mikxk = ∑k (M⋅k)ixk.
From this we can conclude that Mx is a linear combination of columns of M: Mx = ∑k xkM⋅k. Example:
![\[
\left[
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
\right]
\left[
\begin{array}{c}
1 \\ 1 \\ 2
\end{array}
\right]
=
1
\left[
\begin{array}{c}
1 \\
4
\end{array}
\right]
+
1
\left[
\begin{array}{c}
2 \\
5
\end{array}
\right]
+
2
\left[
\begin{array}{c}
3 \\
6
\end{array}
\right]
=
\left[
\begin{array}{c}
1 \\
4
\end{array}
\right]
+
\left[
\begin{array}{c}
2 \\
5
\end{array}
\right]
+
\left[
\begin{array}{c}
7 \\
12
\end{array}
\right]
=
\left[
\begin{array}{c}
9 \\ 21
\end{array}
\right].
\] \[
\left[
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}
\right]
\left[
\begin{array}{c}
1 \\ 1 \\ 2
\end{array}
\right]
=
1
\left[
\begin{array}{c}
1 \\
4
\end{array}
\right]
+
1
\left[
\begin{array}{c}
2 \\
5
\end{array}
\right]
+
2
\left[
\begin{array}{c}
3 \\
6
\end{array}
\right]
=
\left[
\begin{array}{c}
1 \\
4
\end{array}
\right]
+
\left[
\begin{array}{c}
2 \\
5
\end{array}
\right]
+
\left[
\begin{array}{c}
7 \\
12
\end{array}
\right]
=
\left[
\begin{array}{c}
9 \\ 21
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_1aaee73f4fb494fb3c7b0ad5c2819dd3e22ca22c_p1.png)
The set {Mx} for all x is thus equal to the span of the columns of M; it is called the column space of M.
For yM, where y is a row vector, similar properties hold: we can think of yM either as a row vector of dot-products of y with columns of M or as a weighted sum of rows of M; the proof follows immediately from the above facts about a product of a matrix and a column vector and the fact that yM = (M'y')'. The span of the rows of M is called the row space of M, and equals the set {yM} of all results of multiplying a row vector by M.
156.3. Geometric interpretation
Geometrically, linear transformations can be thought of as changing the basis vectors for a space: they keep the origin in the same place, move the basis vectors, and rearrange all the other vectors so that they have the same coordinates in terms of the new basis vectors. These new basis vectors are easily read off of the matrix representing the linear transformation, since they are just the columns of the matrix. So in this sense all linear transformations are transformations from some vector space to the column space of some matrix.28
This property makes linear transformations popular in graphics, where they can be used to represent a wide variety of transformations of images. Below is a picture of an untransformed image (top left) together with two standard basis vectors labeled x and y. In each of the other images, we have shifted the basis vectors using a linear transformation, and carried the image along with it.29
Note that in all of these transformations, the origin stays in the same place. If you want to move an image, you need to add a vector to everything. This gives an affine transformation, which is any transformation that can be written as f(x) = Ax+b for some matrix A and column vector b.
Many two-dimensional linear transformations have standard names. The simplest transformation is scaling, where each axis is scaled by a constant, but the overall orientation of the image is preserved. In the picture above, the top right image is scaled by the same constant in both directions and the second-from-the-bottom image is scaled differently in each direction.
Recall that the product Mx corresponds to taking a weighted sum of the columns of M, with the weights supplied by the coordinates of x. So in terms of our basis vectors x and y, we can think of a linear transformation as specified by a matrix whose columns tell us what vectors for replace x and y with. In particular, a scaling transformation is represented by a matrix of the form
![\[
\left[
\begin{array}{cc}
s_x & 0 \\
0 & s_y
\end{array}
\right],
\] \[
\left[
\begin{array}{cc}
s_x & 0 \\
0 & s_y
\end{array}
\right],
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_32bb44cad426920374134171fa4b22a8084dd87b_p1.png)
where sx is the scale factor for the x (first) coordinate and sy is the scale factor for the y (second) coordinate. Flips (as in the second image from the top on the right] are a special case of scaling where one or both of the scale factors is -1.
A more complicated transformation, as shown in the bottom image, is a shear. Here the image is shifted by some constant amount in one coordinate as the other coordinate increases. Its matrix looks like this:
![\[
\left[
\begin{array}{cc}
1 & c\\
0 & 1
\end{array}
\right].
\] \[
\left[
\begin{array}{cc}
1 & c\\
0 & 1
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_f856545703bcbfd80c5709a2127e3c370a99e7ba_p1.png)
Here the x vector is preserved: (1, 0) maps to the first column (1, 0), but the y vector is given a new component in the x direction of c, corresponding to the shear. If we also flipped or scaled the image at the same time that we sheared it, we could represent this by putting values other than 1 on the diagonal.
For a rotation, we will need some trigonometric functions to compute the new coordinates of the axes as a function of the angle we rotate the image by. The convention is that we rotate counterclockwise: so in the figure above, the rotated image is rotated counterclockwise approximately 315° or -45°. If Θ is the angle of rotation, the rotation matrix is given by
![\[
\left[
\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}
\right].
\] \[
\left[
\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}
\right].
\]](/pinewiki/LinearAlgebra?action=AttachFile&do=get&target=latex_8728eae52a506f5846d990a12d77113d3335fa62_p1.png)
For example, when Θ = 0°, then we have cos Θ = 1 and sin Θ = 0, giving the identity matrix. when Θ = 90°, then cos Θ = 0 and sin Θ = 1, so we rotate the x axis to the vector (cos Θ, sin Θ) = (0, 1) and the y axis to (-sin Θ, cos Θ) = (-1, 0). This puts the x axis pointing north where the y axis used to be, and puts the y axis pointing due west.
156.4. Rank and inverses
The dimension of the column space of a matrix—or, equivalently, the dimension of the range of the corresponding linear transformation—is called the rank. The rank of a linear transformation determines, among other things, whether it has an inverse.
- Claim
If f:ℝn→ℝm is a linear transformation with an inverse f-1, then we can show all of the following:
f-1 is also a linear transformation.
n = m, and f has full rank, i.e., rank(f) = rank(f-1) = m.
- Proof
Let x and y be elements of codomain(f) and let a be a scalar. Then f(af-1(x)) = a(f(f-1(x))) = ax, implying that f-1(ax) = af-1(x). Similarly, f(f-1(x)+f-1(y)) = f(f-1(x)) + f(f-1(y)) = x+y, giving f-1(x+y) = f-1(x) + f-1(y). So f-1 is linear.
Suppose n < m. Pick any basis ei for ℝn, and observe that { f(ei) } spans range(f) (since we can always decompose x as ∑ aiei to get f(x) = ∑ aif(ei)). So the dimension of range(f) is at most n. If n < m, then range(f) is a proper subset of ℝm (otherwise it would be m-dimensional). This implies f is not surjective and thus has no inverse. Alternatively, if m < n, use the same argument to show that any claimed f-1 isnt. By the same argument, if either f or f-1 does not have full rank, it's not surjective.
The converse is also true: If f:ℝn→ℝn has full rank, it has an inverse. The proof of this is to observe that if dim(range(f)) = n, then range(f) = ℝn (since ℝn has no full-dimensional subspaces). So in particular we can take any basis { ei } for ℝn and find corresponding { xi } such that f(xi) = ei. Now the linear transformation that maps ∑ aiei to ∑ aixi is an inverse for f, since f(∑ aixi) = ∑ aif(xi) = ∑ aiei.
156.5. Projections
Suppose we are given a low-dimensional subspace of some high-dimensional space (e.g. a line (dimension 1) passing through a plane (dimension 2)), and we want to find the closest point in the subspace to a given point in the full space. The process of doing this is called projection, and essentially consists of finding some point z such that (x-z) is orthogonal to any vector in the subspace.
Let's look at the case of projecting onto a line first, then consider the more general case.
A line consists of all points that are scalar multiples of some fixed vector b. Given any other vector x, we want to extract all of the parts of x that lie in the direction of b and throw everything else away. In particular, we want to find a vector y = cb for some scalar c, such that (x-y)⋅b = 0. This is is enough information to solve for c.
We have (x-cb)⋅b = 0, so x⋅b = c(b⋅b) or c = (x⋅b)/(b⋅b). So the projection of x onto the subspace { cb | c ∈ ℝ } is given by y = b(x⋅b)/(b⋅b) or y = b(x⋅b)/‖b‖2. If b is normal (i.e. if ‖b‖ = 1), then we can leave out the denominator; this is one reason we like orthonormal bases so much.
Why is this the right choice to minimize distance? Suppose we pick some other vector db instead. Then the points x, cb, and db form a right triangle with the right angle at cb, and the distance from x to db is ‖x-db‖ = √(‖x-cb‖2+‖cb-db‖2) ≥ ‖x-cb‖.
But now what happens if we want to project onto a larger subspace? For example, suppose we have a point x in three dimensions and we want to project it onto some plane of the form { c1b1 + c2b2 }, where b1 and b2 span the plane. Here the natural thing to try is to send x to y = b1(x⋅b1)/‖b1‖2 + b2(x⋅b2)/‖b2‖2. We then want to argue that the vector (x-y) is orthogonal to any vector of the form c1b1 + c2b2. As before, (x-y) is orthogonal to any vector in the plane, it's orthogonal to the difference between the y we picked and some other z we didn't pick, so the right-triangle argument again shows it gives the shortest distance.
Does this work? Let's calculate: (x-y)⋅(c1b1 + c2b2) = x⋅(c1b1 + c2b2) - (b1(x⋅b1)/‖b1‖2 + b2(x⋅b2)/‖b2‖2)⋅(c1b1 + c2b2) = c1(x⋅b1 - (b1⋅b1)(x⋅b1)/(b1⋅b1)) + c2(x⋅b2 - (b2⋅b2)(x⋅b2)/(b2⋅b2)) - c1(b1⋅b2)(x⋅b1)/(b1⋅b1) - c2(b1⋅b2)(x⋅b2)/(b2⋅b2). The first two terms cancel out very nicely, just as in the one-dimensional case, but then we are left with a nasty (b1⋅b2)(much horrible junk) term at the end. It didn't work!
So what do we do? We could repeat our method for the one-dimensional case and solve for c1 and c2 directly. This is probably a pain in the neck. Or we can observe that the horrible extra term includes a (b1⋅b2) factor, and if b1 and b2 are orthogonal, it disappears. The moral: We can project onto a 2-dimensional subspace by projecting independently onto the 1-dimensional subspace spanned by each basis vector, provided the basis vectors are orthogonal. And now we have another reason to like orthonormal bases.
This generalizes to subspaces of arbitrary high dimension: as long as the bi are all orthogonal to each other, the projection of x onto the subspace <bi> is given by ∑ bi(x⋅bi)/‖bi‖2. Note that we can always express this as matrix multiplication by making each row of a matrix B equal to one of the vectors bi/‖bi‖2; the product Bx then gives the coefficients for the basis elements in the projection of x, since we have already seen that multiplying a matrix by a column vector corresponds to taking a dot product with each row. If we want to recover the projected vector ∑ cibi we can do so by taking advantage of the fact that multiplying a matrix by a column vector also corresponds to taking a linear combination of columns: this gives a combined operation of B'Bx which we can express as a single projection matrix P = B'B. So projection corresponds to yet another special case of a linear transformation.
One last detail: suppose we aren't given orthonormal bi but are instead given some arbitrary non-orthogonal non-normal basis for the subspace. Then what do we do?
The trick here is to use a technique called Gram-Schmidt orthogonalization. This constructs an orthogonal basis from an arbitrary basis by induction. At each step, we have a collection of orthogonalized vectors b1...bk and some that we haven't processed yet ak+1...am; the induction hypothesis says that the b1...bk vectors are (a) orthogonal and (b) span the same subspace as a1...ak. The base case is the empty set of basis vectors, which is trivially orthogonal and also trivially spans the subspace consisting only of the 0 vector. We add one new vector to the orthogonalized set by projecting ak+1 to some point c on the subspace spanned by b1...,bk; we then let bk+1 = ak+1-c. This new vector is orthogonal to all of b1...bk by the definition of orthogonal projection, giving a new, larger orthogonal set b1...bk+1. These vectors span the same subspace as a1...ak+1 because we can take any vector x expressed as ∑ ciai, and rewrite it as ∑[i=1..k] cibi + ck+1(c+bk+1), and in the second term ck+1c reduces to a linear combination of b1...bk; the converse essentially repeats this argument in reverse. It follows that when the process completes we have an orthogonal set of vectors b1...bm that span precisely the same subspace as a1...am, and we have our orthogonal basis. (But not orthonormal: if we want it to be orthonormal, we divide each bi by ‖bi‖ as well.)
157. Further reading
Linear algebra is vitally important in ComputerScience: it is a key tool in graphics, scientific computing, robotics, neural networks, and many other areas. If you do further work in these areas, you will quickly find that we have not covered anywhere near enough linear algebra in this course. Your best strategy for remedying this deficiency may be to take an actual linear algebra course; failing that, a very approachable introductory text is Linear Algebra and Its Applications, by Gilbert Strang. You can also watch an entire course of linear algebra lectures through YouTube: http://www.youtube.com/view_play_list?p=E7DDD91010BC51F8.
Some other useful books on linear algebra:
Golub and van Loan, Matrix Computations. Picks up where Strang leaves off with practical issues in doing computation.
Halmos, Finite-Dimensional Vector Spaces. Good introduction to abstract linear algebra, i.e. properties of vector spaces without jumping directly to matrices.
Matlab (which is available on the Zoo machines: type matlab at a shell prompt) is useful for playing around with operations on matrices. There are also various non-commercial knockoffs like Scilab or Octave that are not as comprehensive as Matlab but are adequate for most purposes. Note that with any of these tools, if you find yourselves doing lots of numerical computation, it is a good idea to talk to a numerical analyst about round-off error: the floating-point numbers inside computers are not the same as real numbers, and if you aren't careful about how you use them you can get very strange answers.
In this context, finite means that there is no way to put the set in one-to-one correspondence with one of its proper subsets. (1)
The technical requirements for this to work are stated in Theorem 4 on page 427 of LevitinBook. (2)
Of course, just setting up a recurrence doesn't mean it's going to be easy to actually solve it. (3)
It's even easier to assume that A∩B=∅ always, as I did in an earlier version of these notes and in a similar example in class on 2008-10-08, but for k=1 any sequence is both increasing and nonincreasing, since there are no pairs of adjacent elements in a 1-element sequence to violate the property. (4)
Without looking at the list, can you say which 3 of the 62=36 possible length 2 sequences are missing? (5)
We are using word in the combinatorial sense of a finite sequence of letters (possibly even the empty sequence) and not the usual sense of a finite, nonempty sequence of letters that actually make sense. (6)
The justification for doing this is that we know that a finite sequence really has a finite sum, so the "singularity" appearing at z=1 in e.g. (1-zn+1)/(1-z) is an artifact of the generating-function representation rather than the original series—it's a removable_singularity that can be replaced by the limit of f(x)/g(x) as x→c. (7)
Technically, the function f(x) = Pr[X=x] is the mass function for X while the distribution function is F(x) = Pr[X≤x], but we can easily convert from one to the other. (8)
Technically, this will work for any values we can add and multiply by probabilities. So if X is actually a vector in ℝ3 (for example), we can talk about the expectation of X, which in some sense will be the average position of the location given by X. (9)
OK, my intuitions. (10)
The detail we are sweeping under the rug here is what makes a subset of the codomain measurable. The essential idea is that we also have a σ-algebra F' on the codomain, and elements of this codomain σ-algebra are the measurable subsets. The rules for simple random variables and real-valued random variables come from default choices of σ-algebra. (11)
Curious fact: two of these unpopular vegetables are in fact cultivars of the same species Brassica oleracea of cabbage. (12)
You don't really need to know about Zorn's Lemma, but if you are curious, Zorn's Lemma says that if (S,<) is any poset, and every totally-ordered subset S' of S has an upper bound x (i.e. there exists some x such that y ≤ x for all y in S'), then S has a maximal element. Applying this to partial orders, let R be some partial order on a set A, and let S = { R' | R' is a partial order on A with R subset of R' }, ordered by subset. Now given any chain of partial orders R1, R2, ..., where each partial order extends R and is a subset of the next, their union is also a partial order (this requires proof) and any Ri is ≤ the union. So S has a maximal element R*. If R* is not a total order, we can find a bigger element R** by breaking a tie between some pair of incomparable elements, which would contradict maximality. So R* is the total order we are looking for. (13)
Proof: We can prove that any nonempty S⊆ℕ has a minimum in a slightly roundabout way by induction. The induction hypothesis is that if S contains some element y less than or equal to x, then S has a minimum element. The base case is when x=0; here x is the minimum. Suppose now that the claim holds for x. Suppose also that S contains some element y ≤ x+1. If there is some y ≤ x, then S has a minimal element by the induction hypothesis. The alternative is that there is no y in S such that y ≤ x, but there is a y in S with y ≤ x+1. This y must be equal to x+1, and it itself is the minimal element. (14)
The product of two lattices with lexicographic order is not always a lattice. For example, consider the lex-ordered product of ({0,1}, ⊆) with (ℕ, ≤). For the elements x=({0}, 0) and y=({1},0) we have that z is lower bound on x and y iff z is of the form (∅, k) for some k∈ℕ. But there is no greatest lower bound for x and y because we can always choose a bigger k. (15)
This table was generated by running attachment:multiplication.py and then doing some editing to mark the ones. (16)
Fermat proved FLT before Euler generalized it to composite m, hence the two names. (17)
Sometimes reversed composition, so that πρ means do π then ρ rather than the usual do ρ then π; watch out for different authors handling this in different ways. (18 19)
Containing more than just the identity element. (20)
Not equal to the entire group. (21)
In this case, nontrivial means that the homomorphism doesn't send everything to e. (22)
Also called pseudo-rings. You do not need to remember this definition. (23)
The convention for both indices and dimension is that rows come before columns. (24)
The original image is taken from http://www.hertfordshire-genealogy.co.uk/data/books/books-3/book-0370-cooke-1807.htm. As an exact reproduction of a public domain document, this image is not subject to copyright in the United States. (25)
The tedious details: to multiple row r by a, use a matrix B with Bii = 1 when i≠r, Brr=a, and Bij=0 for i≠j; to add a times row r to row s, use a matrix B with Bii = 1 when i≠r, Brs = a, and Bij=0 for all other pairs ij; to swap rows r and s, use a matrix B with Bii = 1 for i∉{r,s}, Brs = Bsr = 1, and Bij for all other pairs ij. (26)
Technical note: If the set of vectors xi is infinite, then we may choose to only permit linear combinations with a finite number of nonzero coefficients. We will generally not consider vector spaces big enough for this to be an issue. (27)
We are abusing notation by not being specific about how long ei is; we will use the same expression to refer to any column vector with a 1 in the i-th row and zeros everywhere else. We are also moving what would normally be a subscript up into the superscript position to leave room for the row index—this is a pretty common trick with vectors and should not be confused with exponentiation. (28)
The situation is slightly more complicated for infinite-dimensional vector spaces, but we will try to avoid them. (29)
The thing in the picture is a Wooper, which evolves into a Quagsire at level 20. This evolution is not a linear transformation. (30)
